Практическое задание к теме 3

По территориям региона приводятся данные за 2002X г.

Задание

1. 
   Построить линейное уравнение парной регрессии yот x.
   
2. 
   Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
   
3. 
   Оценить статистическую значимость параметров регрессии и корреляции с помощью F-критерия Фишера и t-критерия Стьюдента.
   
4. 
   Выполнить прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от среднего уровня.
   
5. 
   Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
   
6. 
   На одном графике отложить исходные данные и теоретическую прямую.
   

Таблица3. Исходные данные для построения линейное уравнение парной регрессии(в каждом варианте к прожиточному минимуму и заработной плате надо прибавить число 10*k, где k – порядковый номер студента в журнале группы).

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., x	Среднедневная заработная плата, руб., y
1	101	144
2	97	151
3	105	166
4	99	159
5	113	163
6	120	179
7	92	155
8	110	172
9	91	147
10	109	174
11	102	147
12	131	182

Решение: Для предварительного определения вида связи между указанными признаками построим корреляционное поле.

Получим следующий рисунок.



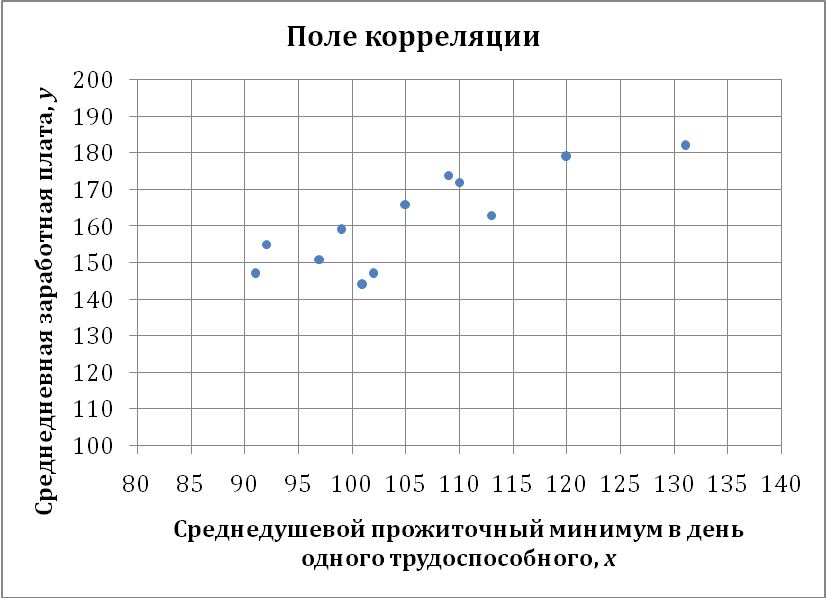
По внешнему виду поля корреляции предположим

---

, что зависимость между указанными показателями линейная, т.е. вида y = a + bx.

Для расчета параметров уравнения линейной регрессии и коэффициента парной корреляции составим таблицу.

№ п/п	x	y	x2	y2	xy
1	101	144	10201	20736	14544
2	97	151	9409	22801	14647
3	105	166	11025	27556	17430
4	99	159	9801	25281	15741
5	113	163	12769	26569	18419
6	120	179	14400	32041	21480
7	92	155	8464	24025	14260
8	110	172	12100	29584	18920
9	91	147	8281	21609	13377
10	109	174	11881	30276	18966
11	102	147	10404	21609	14994
12	131	182	17161	33124	23842
	1270	1939	135896	315211	206620
Среднее	105,8	161,6	11324,7	26267,6	17218,3

---

Вычислим коэффициент парной корреляции:

= 0,838.

Можно сказать, что между рассматриваемыми признаками существует прямая тесная корреляционная связь.

Значения параметров a и b линейной модели определим, используя данные предыдущей таблицы.

= 0,95.

= 161,6 – 0,95105,8 = 61,33.

Уравнение регрессии имеет вид: .

Для оценки качества модели вычислим среднюю ошибку аппроксимации. Вычислим по построенному уравнению теоретические значения . Составим расчетную таблицу.

№ п/п	x	y
1	101	144	157,0	8,28
2	97	151	153,2	1,45
3	105	166	160,8	3,24
4	99	159	155,1	2,51
5	113	163	168,4	3,19
6	120	179	175,0	2,28
7	92	155	148,5	4,39
8	110	172	165,5	3,91
9	91	147	147,5	0,36
10	109	174	164,6	5,72
11	102	147	158,0	6,93
12	131	182	185,4	1,85
Сумма	1270	1939	1939	44,11

---

Рассчитаем среднюю ошибку аппроксимации по формуле

= 44,11 : 12 = 3,68%.

Таким образом, можно сказать, что построенное уравнение достаточно точно описывает зависимость между рассматриваемыми показателями.

Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

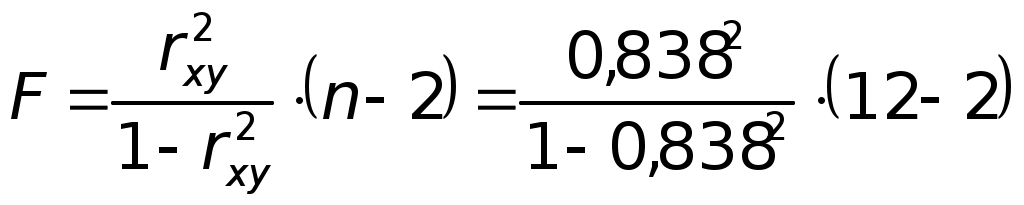= 23,58.

Для  = 0,05; k₁ = m = 1, k₂ = n – m – 1 = 12 – 1 – 1 = 10 F_табл = 4,96.

Поскольку данное значение превышает табличное, коэффициент корреляции является статистически значимым.

Оценим статистическую значимость параметров регрессии с помощью t-критерия Стьюдента. Вычислим стандартные ошибки m_a и m_b.



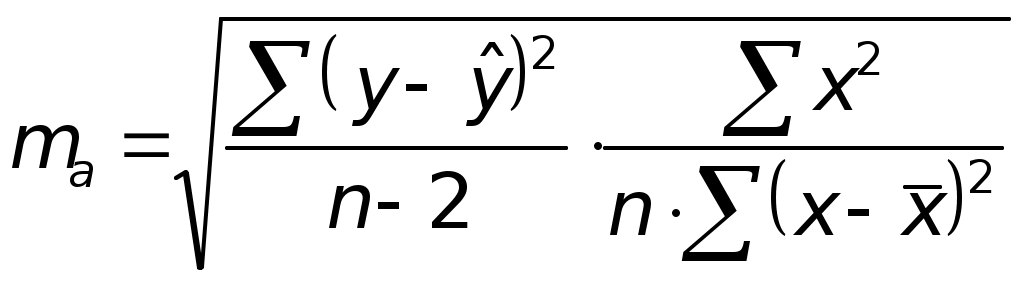
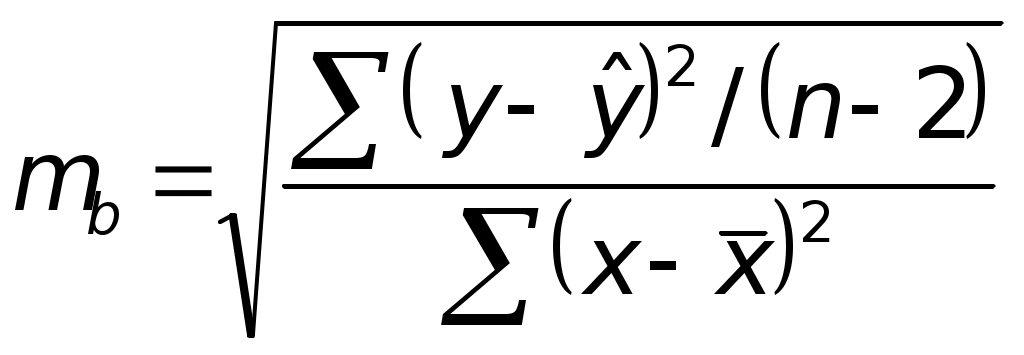
Составим вспомогательную таблицу.

№ п/п	x	y
1	101	144	157,0	169,131	23,36
2	97	151	153,2	4,911	78,03
3	105	166	160,8	27,103	0,69
4	99	159	155,1	15,128	46,69
5	113	163	168,4	28,857	51,36
6	120	179	175,0	15,980	200,69
7	92	155	148,5	42,511	191,36
8	110	172	165,5	41,859	17,36
9	91	147	147,5	0,284	220,03
10	109	174	164,6	88,682	10,03
11	102	147	158,0	119,952	14,69
12	131	182	185,4	11,710	633,36
	1270	1939	1939	566,108	1487,67

---

Определим фактические значения t-критерия Стьюдента.



При уровне значимости  = 0,05 и числе степеней свободы  = 12 – 1 = 11 значение t-критерия составляет t = 2,23. Поскольку фактические значения критериев превышают табличное значение, то оба коэффициента являются статистически значимыми.

Выполним прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x , составляющем 107% от среднего уровня.

Прогнозное значение фактора x после увеличения на 7% от среднего уровня составит:

= 105,8  1,07 = 113,24 руб.

Подставим это значение в уравнение линейной регрессии.

Получим: = 168,6 руб.

Определим доверительный интервал прогноза для уровня значимости  = 0,05.

Вычислим среднюю стандартную ошибку прогноза по следующей формуле:

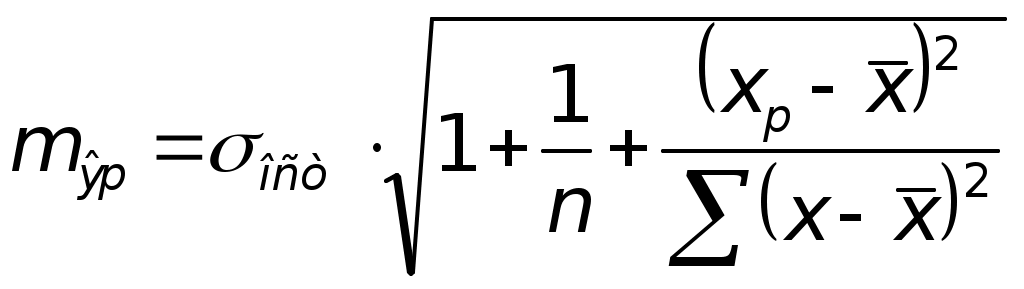, где

= 7,524.

= 7,96.

Найдем предельную ошибку прогноза , где для доверительной вероятности 0,95 значение t составляет 2,23.

= 2,23  7,96 = 17,74.

Запишем доверительный интервал прогноза.

= 168,6 – 17,74 = 150,86 руб.

= 168,6 + 17,74 = 186,34 руб.

Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение среднедневной заработной платы по всей совокупности будет находиться в пределах от 150,86 до 186,34 руб.

---

Смотрите также файлы

• Реферат имеет строго определенную структуру.docx

• Практические задания по 1 теме.docx

• 1. Какие традиционные российские духовнонравственные ценности сформулированы в Стратегии национальной безопасности Российской Федерации.docx

• История Казахстана иа2023 (по обновленной учебной программе).pdf

• Две формы существования права Естественное право.docx