dr=[????????⃗,r] |dr|=????????⃗*r*sin(????????⃗,r) Если вращать буравчик от ????????⃗ к r, поступательное движение буравчика укажет направление dr.

v=????⃗*r - линейная скорость точек, находящихся на разных расстояниях от оси вращения.

a=????⃗*r - тангенциальное ускорение точки, находящейся на разных расстояниях от оси

12) Момент импульса L материальной точки относит. точки О - ВФВ, характеризующая вращательное движение МТ и равная векторному произведению вектора F, проведённого от т. О к МТ на импульс вектора p МТ.



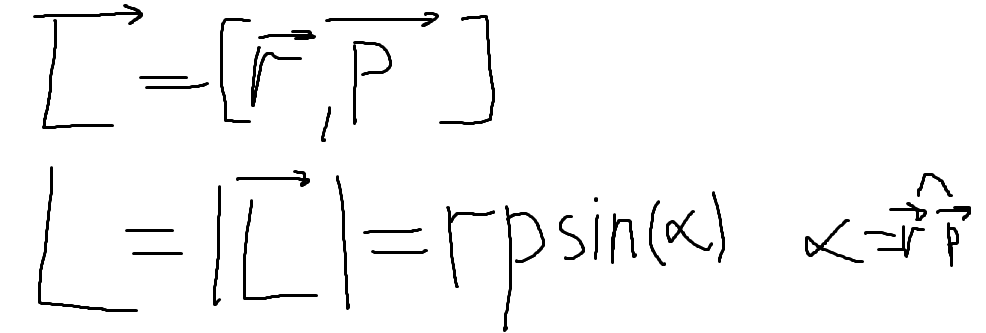
[Вектор L можно определить по правилу буравчика (вращать от r к p) и левой руки (4 пальца по r, p входит в ладонь)]

Момент силы М относительно т. О - ВФВ, характеризующая вращательное движение силы и равная векторному произведению r, проведенного от т. О к т. приложения силы на силу F.



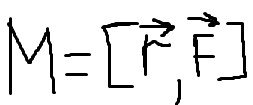
[Направление вектора М можно определить по тем же правилам, что и для L]

13) Основное уравнение динамики вращательного движения АТТ

14) Момент силы относительно оси вращения - СФВ равная проекции на эту ось вектора момента силы М, определенного относительно произвольной точки О, взятой на данной оси. Аналогично для Момента импульса.

Момент инерции I - ФВ, являющаяся мерой инертности тела при его вращательном движении. Для АТТ: I = Σm(r)^2

15) Момент инерции I - физическая величина, являющаяся мерой инертности тела при его вращательном движении. Для МТ: I=mr^2, где m-масса МТ, r-радиус вращения. Момент инерции однородного стержня, вращающегося вокруг оси С, перпендикулярный стержню и проходящий через его центр - ось, проходящая через центр масс тела. Разобьем стержень на бесконечно малые цилиндры толщиной dr, тогда dV=Sdr.
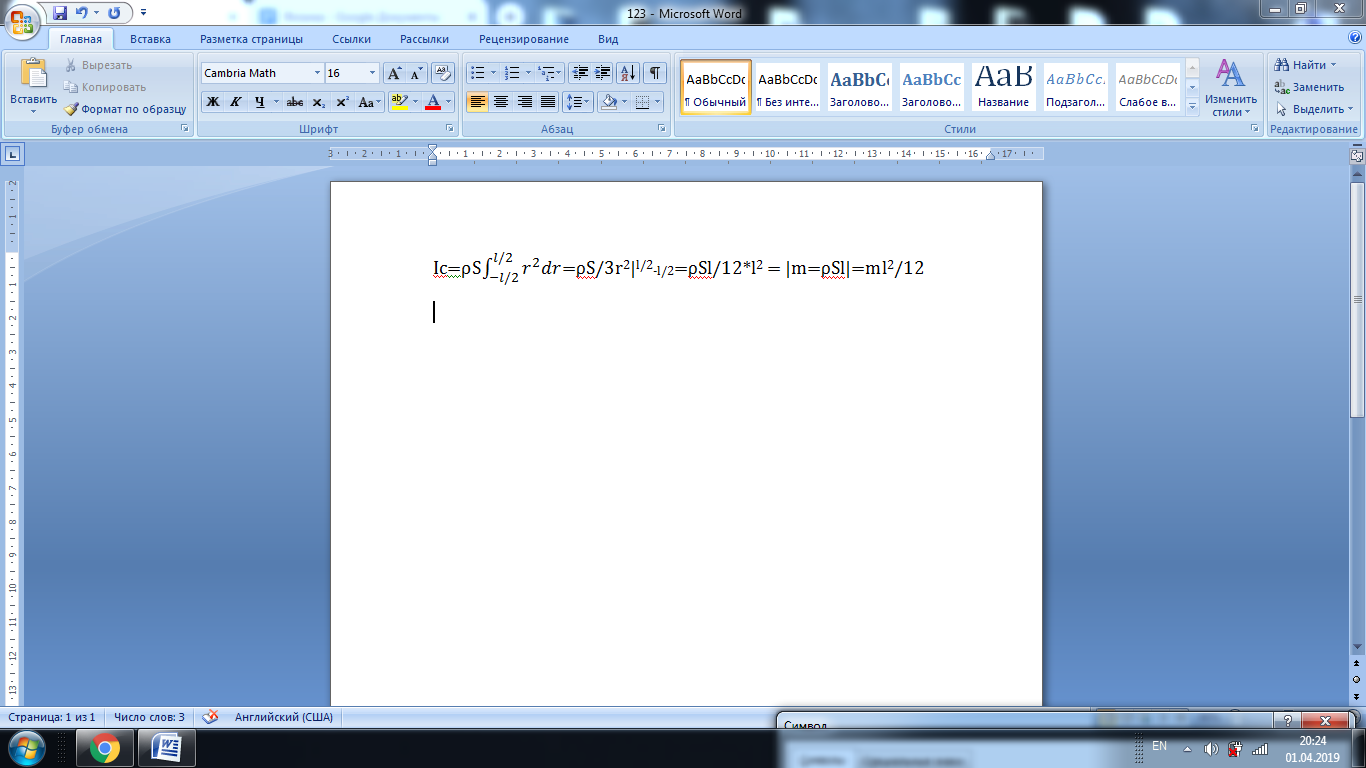
Момент инерции стержня относительно оси О, проходящей через его край, но параллельно оси С.

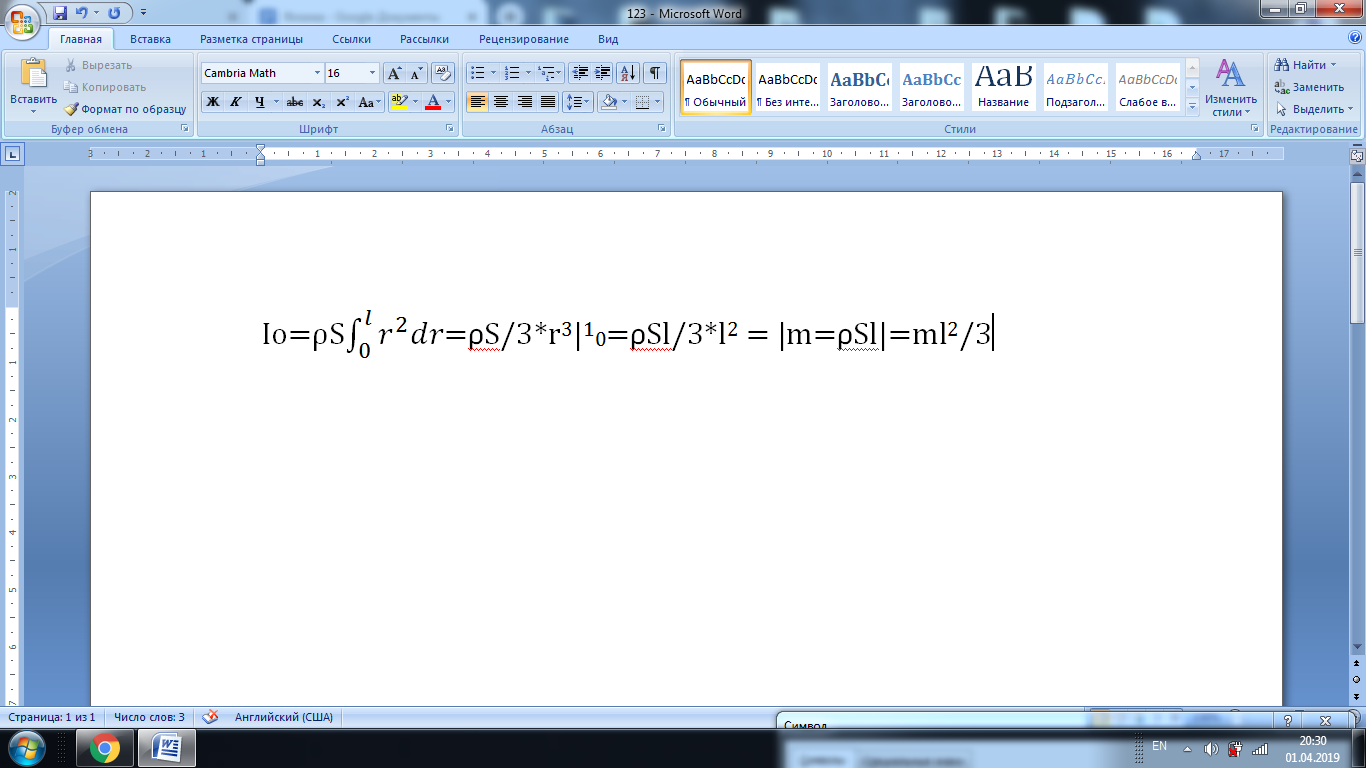
Момент инерции диска: ½*mr^2

Момент инерции шара: ⅖*mr^2

Теорема Штейнера: момент инерции I0 относительно произвольной оси равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями. I0=Ic+ma^2

---

16) Закон сохранения момента импульса.
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным соединением:

Модуль вектора момента импульса

Моментом импульса относительно неподвижной точки z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси.

Для совокупности точек можно записать:


зная, что :

Продифференцировав обе части по времени:

, итого
Это еще одна форма уравнения динамики вращательного движения твердого тела.
В замкнутой системе момент внешних сил М=0, и , откуда:

L = const

Что представляет закон сохранения момента импульса.


17)

18) Макросостояние определяется p, V, T.

Микросостояние определяется заданием координат и импульсов всех частиц.

Предмет молекулярной физики - физические свойства макроскопических систем как результат рассмотрения движения и взаимодействия частиц, из которых состоит макросистема с использованием методов теории вероятности и статистики.
Идеа́льный газ — теоретическая математическая модель газа; в которой пренебрегают размерами частиц газа, не учитывают силы взаимодействия между частицами газа, предполагая, что средняя кинетическая энергия частиц много больше энергии их взаимодействия, и считают, что столкновения частиц газа между собой и со стенками сосуда абсолютно упругие.
19) Вероятность и плотность вероятности. Закон (распределение) Максвелла по скоростям молекул идеального газа.

Вероятность того, что скорость молекулы находится в интервале (v; v+dv):

---

Таким образом f(v) - функция распределения молекул ИГ по скоростям - плотность вероятности:



В результате многократных соударений в каждой стороне движется одинаковое количество молекул. Первым, кто вывел, что со временем устанавливается стационарное количество молекул, движущихся с одинаковой скоростью, был Дж. Максвелл. Он допускал, что:

• 
  Газ в беспорядочном движении при одинаковой температуре.
  
• 
  Силовые поля на газ не действуют.
  

Закон Максвелла описывается функцией распределения молекул по скоростям. Если взять небольшой промежуток, то на каждый промежуток будет приходится определенное количество молекул, имеющих скорость, обозначенную интервалом.


Данная формула показывает отношение молекул с определенной скоростью ко всем.

Применяя методы теории вероятностей, Максвелл нашел f(v) - закон о распределении молекул идеального газа по скоростям:



Для любой функции распределения (молекул ИГ по скоростям в частности) выполняются условия нормальной нормировки:



Её физический смысл - с вероятностью 100% скорость данной молекулы найдётся на интервале (0;беск).
20) Наиболее вероятная скорость молекул - это скорость, при которой функция распределения молекул по скорости максимальна. Наиболее вероятная скорость находится по формуле:



Средняя скорость молекул:

=(∑Vi)/N=∫(VdN(V)/N) (над значком ∑: N Над значком ∫: ∞)

(над значком ∑: i=1 Над значком ∫:0)

Средняя квадратичная скорость молекул:

=√3kT/m0=√3RT/M

Опытная проверка распределения Максвелла (опыт Ламмерта):



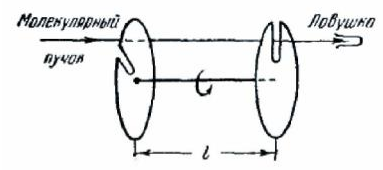
Закон распределения был проверен в опыте Ламмерта (1929 г.), в котором молекулярный пучок пропускался через два вращающихся диска с радиальными щелями, смещенными друг относительно друга на некоторый угол φ (рис. 243). Из числа молекул, пролетевших через щель в первом диске, пролетят через второй диск только те, которые подлетят к нему в тот момент, когда на пути пучка встанет прорезь во втором диске. Более быстрые молекулы достигнут второго диска слишком рано, а более медленные — слишком поздно для того, чтобы пройти через щель. Таким образом, это устройство позволяет выделить из пучка молекулы, обладающие определенным значением скорости (из-за конечной ширины щелей прибор выделяет молекулы, скорости которых лежат в пределах некоторого интервала∆v). Средняя скорость выделяемых прибором молекул может быть найдена из условия, что время t1 за которое молекулы пролетают расстояние l между дисками (t1 =l / v ), должно совпадать со временем t2 за которое диски повернутся на угол φ (t2 =ϕ / ω ).

Приравняв оба времени, получим: v = ωϕl

21)Идеальный газ – модель газа, в рамках которого молекулы и атомы газа представлены в виде очень маленьких (исчезающих размеров) упругих шариков, которые не взаимодействуют друг с другом (без непосредственного контакта), а только сталкиваются.

Основное уравнение молекулярно-кинетической теории идеальных газов:



Здесь: V- средняя скорость движения частиц;

n– концентрация частиц газа – количество частиц, приходящихся на единицу объёма; ; единица измерения – .
22) Барометрическая формула- зависимость давления или плотности газа от высоты в поле силы тяжести в стационарных условиях.

Барометрическая формула:



где p — давление газа в слое, расположенном на высоте H, p0 — давление над уровнем моря, M — молярная масса газа, R — универсальная газовая постоянная, T — абсолютная температура.

Ф-я распределения Больцмана:

Распределение Больцмана-концентрация молекул газа под воздействием гравитационного поля в зависимости от высоты.

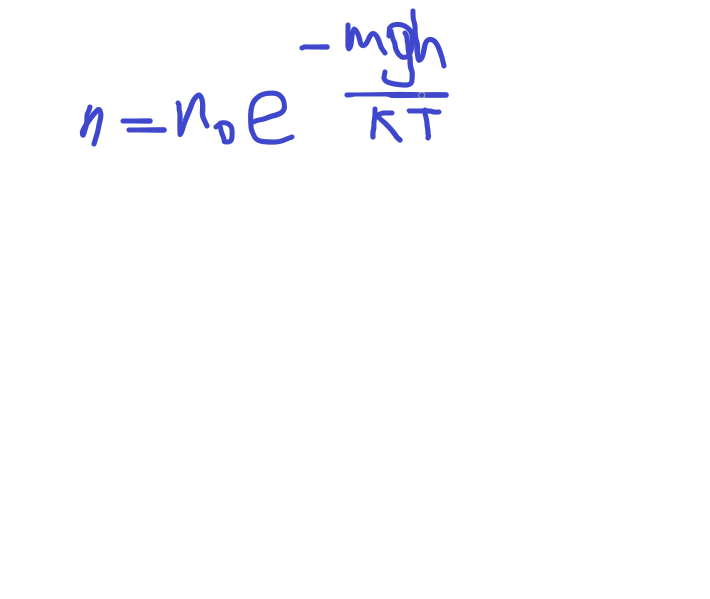
где m— масса молекулы газа, k — постоянная Больцмана.
23)Равновесное состояние состояние системы - состояние, при котором все параметры состояния имеют определенное значение, которые остаются постоянными при неизменных внешних условиях.
Обратимый процесс - это равновесный процесс, который допускает возвращение системы в исходное состояние, при этом в обратном направлении система повторяет все те же стадии пути, что и в прямом
Необратимый процесс - неравновесный; систему невозможно вернуть в исходное состояние. Все реальные процессы в природе необратимые
Круговой процесс - процесс, при котором система, пройдя через ряд состояний возвращается в исходное.
А (в термодинамике) - СФВ, характеризующая процесс обмена энергией между системой и определенными телами, при котором происходят перемещение макроскопических частей тел

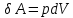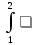A= pdV

24) Внутрення энергия – энергия хаотического (теплового) движениямикрочастиц системы (атомов, молекул) и энергия взаимодействия этих частиц. ????=∑????к+∑????????. Ко внутренней энергии не относятся :

1) Кинетическая энергия движения системы как целого, 2) Потенциальная энергия системы во внешних полях. Количество степеней свободы i – число независимых между собой перемещений механической системы. Степени свободы могут быть поступательными, вращательными, колебательные, а их количество зависит от числа атомов, образующих молекулу. Степень совободы отлична от 0, если соответственные движения изменяет пространственное положение молекул.

Закон Максвела – Больцмана – о равнораспределении энергии по степеням свободы – для системы находящейся в состоянии термодинамического равновесия на каждую постоянную и вращательную степень свободы приходится в среднем кинетическая энергия = kT/2, на каждую колебательную kT. 〈????????0〉=????????2(????пост+????вращ)+????????∗????кол принимая ????кол=0, для одноатомного: 3????????2; для двухатомной 5????????2; трехатомной 3kT. Внутренняя энергия ИГ:????=????〈????ок〉=>????=????????????2(????пост+????вращ)=????????2????????

Если N=Nа, получаем внутр. Энергию 1 моль ИГ ????м=????????????2????????=????2????????. Для произвольного числа молекул ИГ ????=????????????→????=????????????2????????→∆????=????2−????1=????????????2????(????2−????1)не зависит от того,в результате какого процесса произошло это изменение, т.е. внутренняя энергия – функция состояния.

25) 1-ое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение её внутренней энергии и на совершение ею работы Q=∆U+A.

Теплообмен и его виды: Теплообмен - процесс обмена энергии между системой и телами, при котором не происходит перемещение макроскопических частей системы. Виды теплообмена: теплопроводность, излучение, конвекция.

Теплоемкость - СФВ, равная количеству теплоты, которое нужно сообщить телу, чтобы нагреть его на 1 Кельвин: C=dQ/dT

Удельная теплоемкость - теплоемкость, приходящаяся на единицу массы вещества: C_уд=dQ/mdT

Молярная теплоемкость - теплоемкость, приходящаяся на 1 моль вещества: С_моляр=dQ/νdT
26)Теплоемкость - СФВ, равная отношение количества теплоты, сообщённого газу, к изменению температуры, которое при этом произошло.




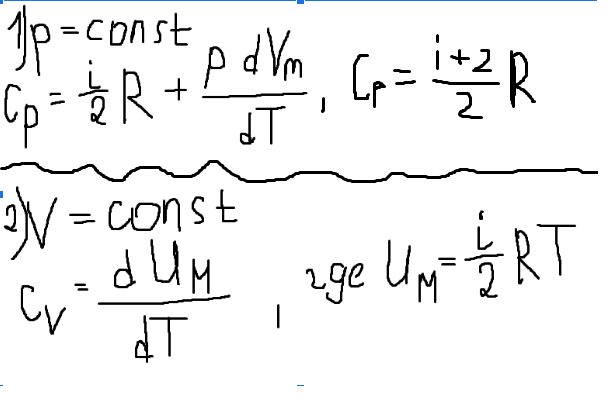
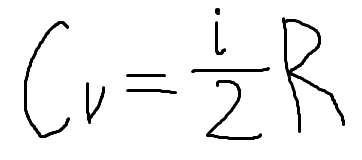
Уравнение Майера :При нагревании газа при p=const теплота расходуется не только на изменение внутренней энергии, но и на совершение работы.

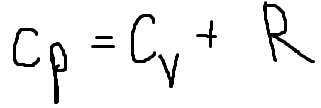
Коэффициент Пуассона (показатель адиабаты):

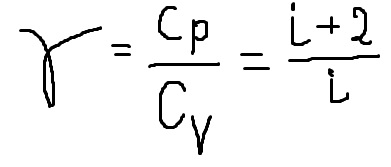
27)Адиабатный процесс – процесс при котором отсутствует теплообмен между системой и окружен телами ????????=0 любой быстропротекающий процесс. ????????????=???????????????????? уравнение адиабатного процесса. ????????=????????+????????=0=>????????=−????????→????=−∆????=????2????????(????1−????2) работа совершенная за счет убыли внутренней энергии. Число степеней свободы и как следствие теплоемкость зависят от температуры.

28) Для любого обратимого цикла ∫????????????=0=>????????=????????????


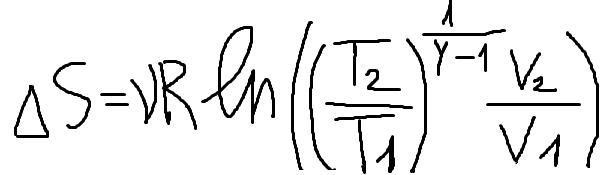
S - энтропия ∆????=∫????????????21 – приращение энтропии {∆????=∫????????????21=[????????=????????+????????]=∫????????????21+∫????????????21{????????=????2????????????????????=2????−1→????????=1????−1????????????????→∆????=????????????−1∫????????????21+∫????????????21

{????????=????????????????=????????????????→????????=????????????????????????=>∆????=????????????−1ln????2????1+????????∫????????????21=>∆????=????????ln(????21????−1∗????2????11????−1∗????1)

При адиабатном процессе ????Q=0 → dS=0 энтропия остается постоянной.Энтропия обладает свойством аддитивности.

Энтропия – СФВ, характеризующая макросостояние системы и является мерой беспорядка в системе ????=????lnΩ формула Больцмана. Энтропия пропорциональна вероятности → в состоянии равновесия, которое является наиболее вероятным, энтропия будет максимальна.

Неравенство Клазиуса: любой необратимый процесс в замкнутой системе происходит так, что энтропия при этом возрастает (при обратимых процессах энтропия остается неизменной).
29) Формулировка Кельвина:невозможен циклический процесс, единственным результатом которого является производство работы за счет уменьшения внутренней энергии только одного теплового резервуара(рис. 11.1).

Формулировка Оствальда: невозможен вечный двигатель второго рода.Вечный двигатель второго рода – это тепловая машина без низкотемпературного резервуара (рис 11.1).

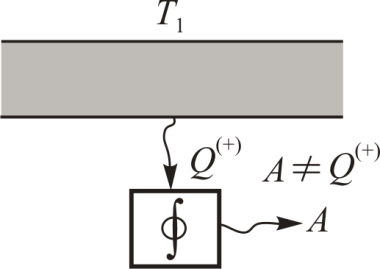
Формулировка Клаузиуса: теплота не может самопроизвольно переходить от тела менее нагретого к более нагретому.
ТЕПЛОВАЯ СМЕРТЬ ВСЕЛЕННОЙ.
После введения Рудольфом Клаузиусом понятия энтропии в 1865 году возникло множество споров, домыслов и теорий, связанных с этим понятием. Одна из них – гипотеза о тепловой смерти Вселенной, сформулированная самим Клаузиусом на основе второго начала термодинамики.
При выводе своей теории Клаузиус прибегал в своих рассуждениях к следующим экстраполяциям (приближениям):

1. 
   Вселенная рассматривается как замкнутая система.
   
2. 
   Эволюция мира может быть описана как смена его состояний.
   

30) Тепловой двигатель - устройство, предназначенное для превращения внутренней энергии топлива в механическую работу.

КПД (коэффициент полезного действия:


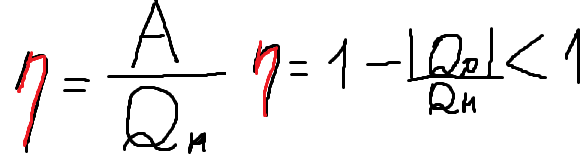
Максимальным КПД обладает тепловой двигатель, работающий по циклу Карно:

---

Смотрите также файлы

• Между человеком образованным и необразованным такая же разница, как между живым и мертвым.docx

• Тарасова Ульяна Алексеевна студентка б группы дневного отделения подпись.pdf

• Пермский государственный гуманитарнопедагогический университет.docx

• Отчет по учебноознакомительной практике на ооо Хоум Кредит энд Финанс Банк.rtf

• Ссылки на запись занятия (19. 04. 2023) vk httpsvk comvideo198655662 456239740listlnnQEhfAfX77mO0Em2Ui Rutube.docx