Вариант 25
З адание 1.

Докажите тождества, используя только определения операций над множествами.
1)

и

и



2)








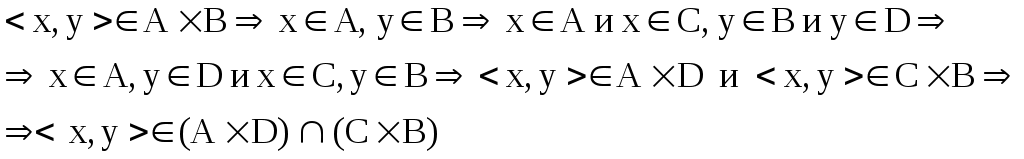
Задание 2.

Докажите утверждение.


Для доказательства утверждения достаточно доказать, что , так как в этом случае между множествами будет установлено взаимно однозначное соответствие, то есть они будут эквивалентны.

Используя арифметику кардинальных чисел, преобразуем левую и правую части к одному виду:





Так как полученные выражения совпадают, то исходные множества эквивалентны.

---

Задание 3.

Докажите методом математической индукции, что кратно 7 для всех n>0.
Найдем базис индукции:

n=1

– кратно 7

Предположим, что кратно 7 для некоторого n.

Докажем, что также кратно 7.


– кратно 7 по предположению индукции

– кратно 7.

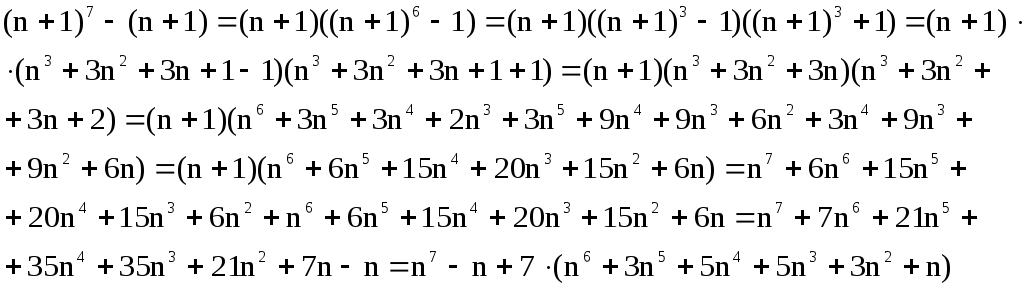
Значит, так как справедливость утверждения доказана для n+1, то верно, что кратно 7 для всех n>0.







Задание 4.

A={a,b,c}, B={1,2,3,4}, Изобразите , графически. Найдите [ ]. Проверьте с помощью матрицы [ ], является ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?












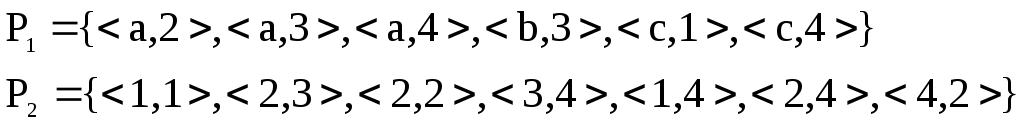
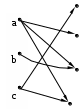
1
2


3
4

[

---

]= [ ]=

[ ]=



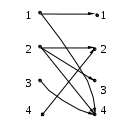
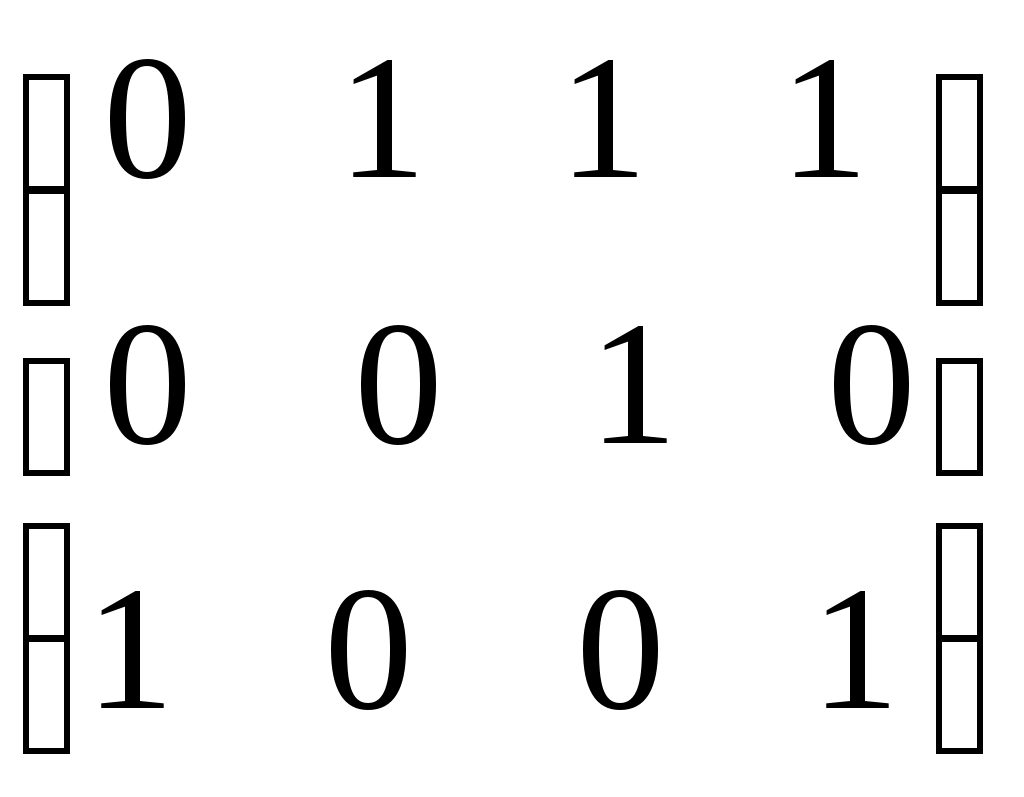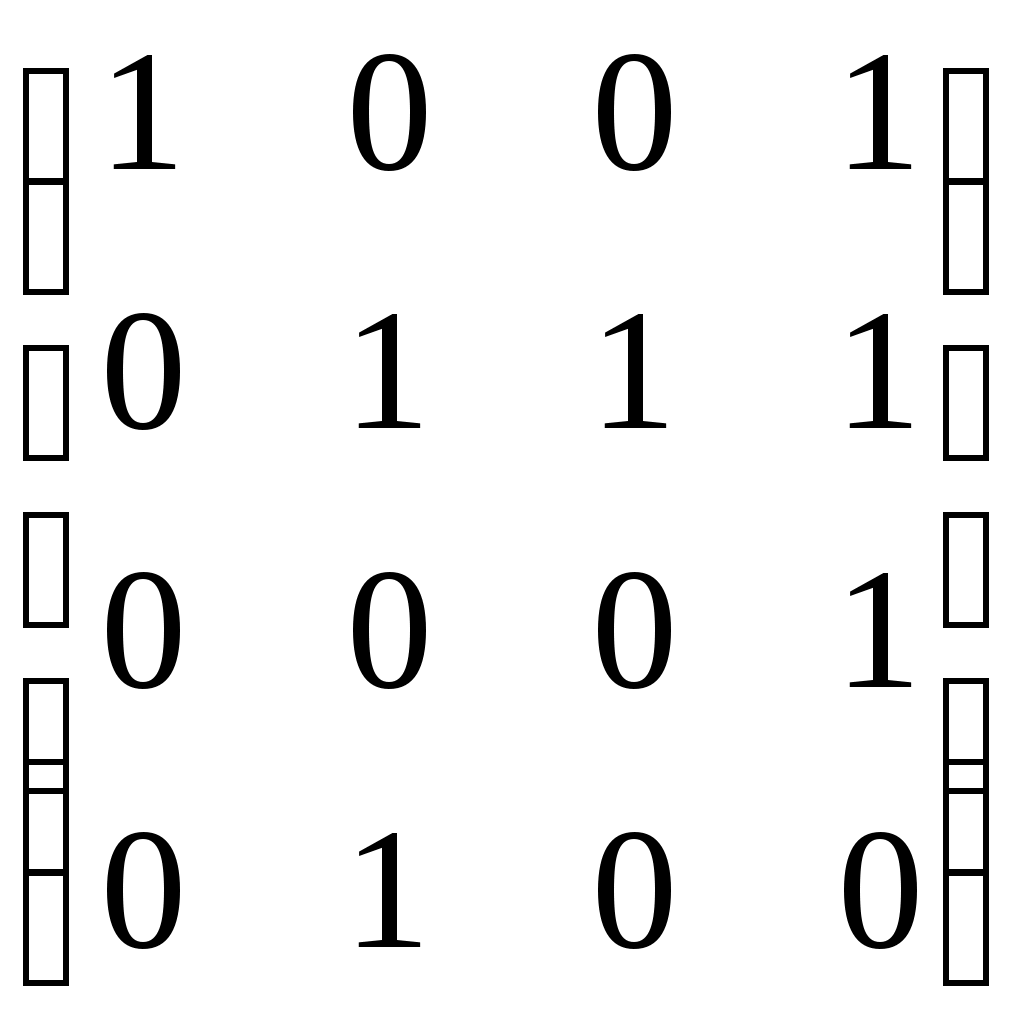
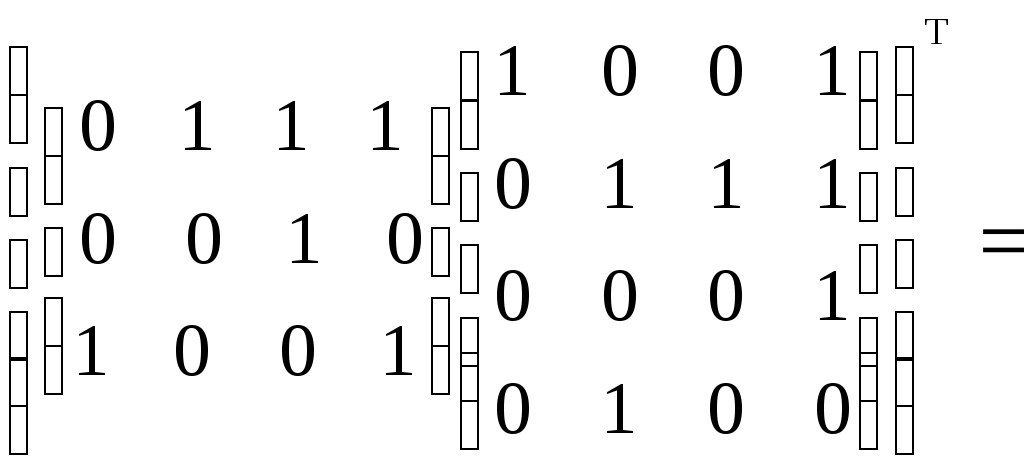
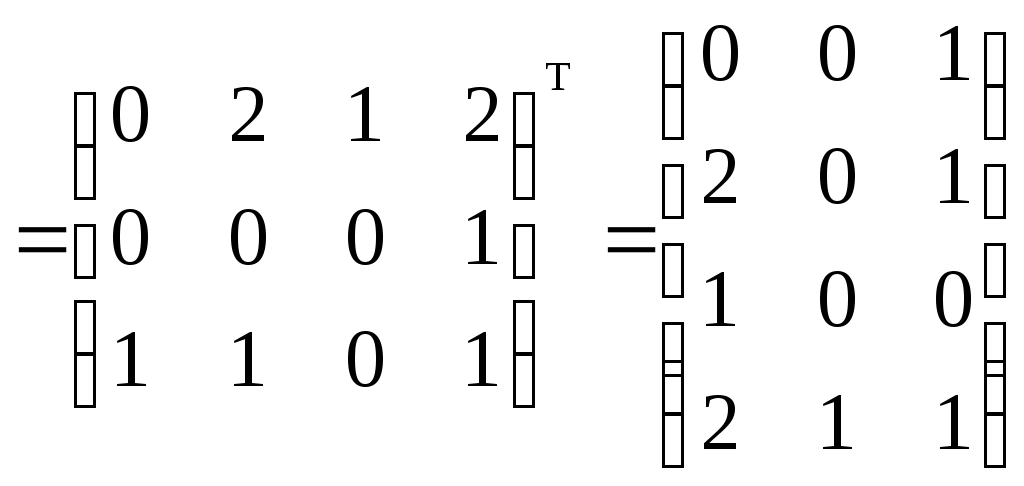
1) 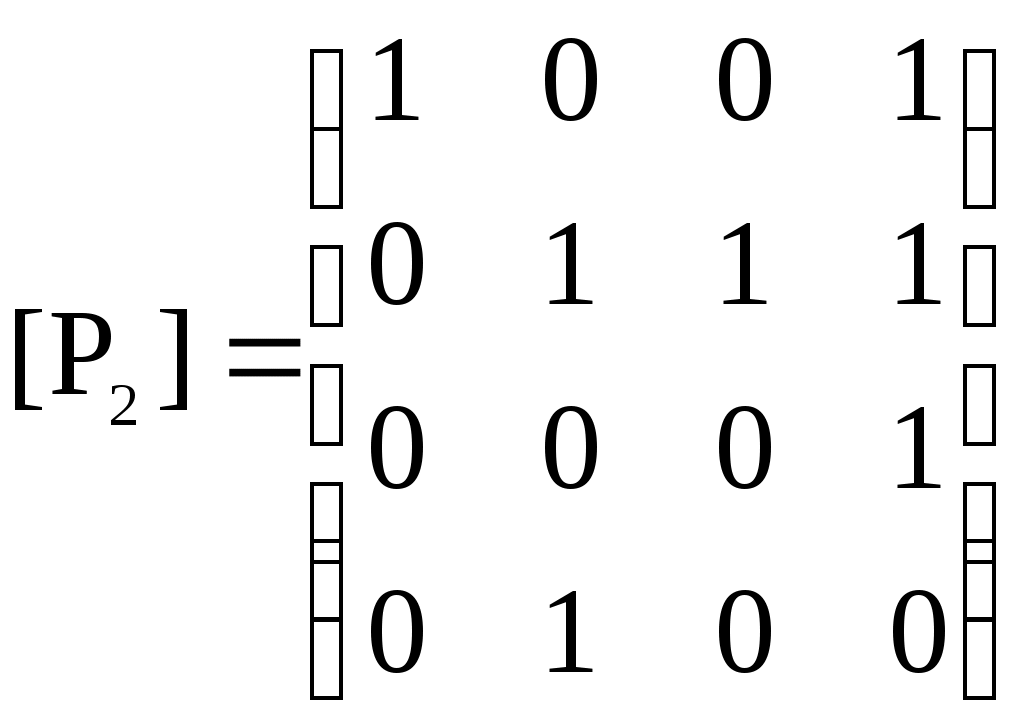– по диагонали есть нули – нерефлексивно.
2) 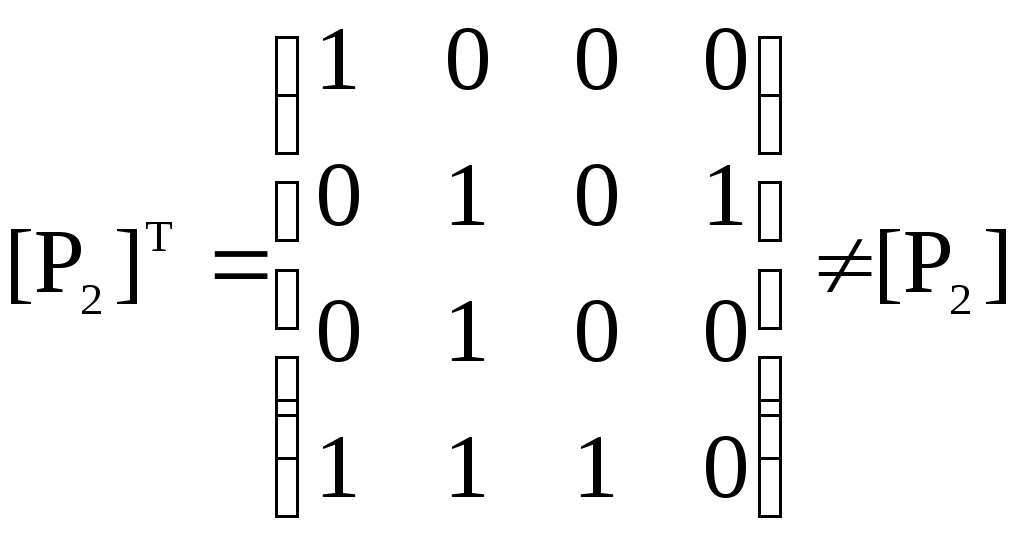– поэтому – несимметрично.
3 ) – не-антисимметрично.

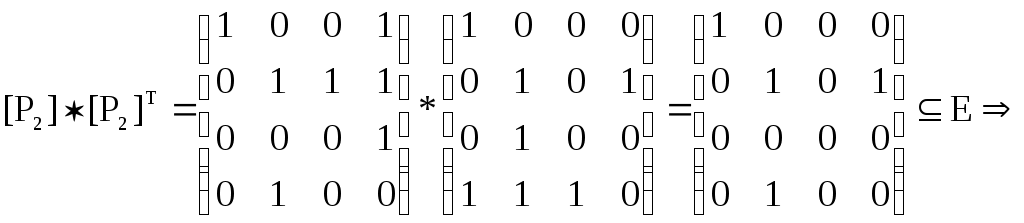
4)






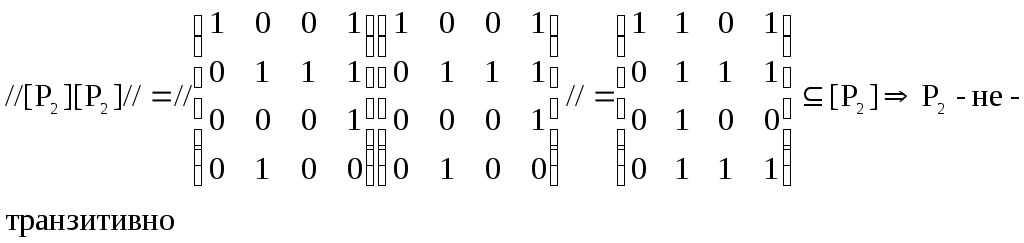
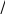
Задание 5.

Найдите область определения, область значений отношения P. Является ли отношение P рефлексивным, симметричным, антисимметричным, транзитивным?


Область определения:



Область значений:



1) Если

P – рефлексивно.

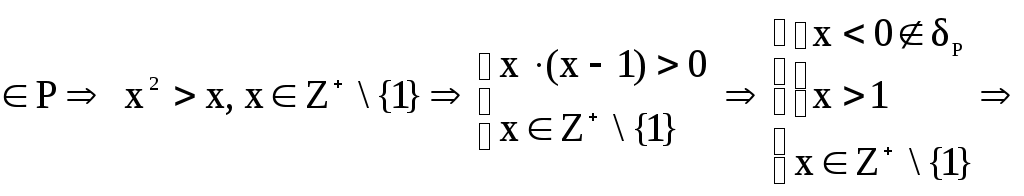
2) Так как то P – несимметрично

3) Пусть

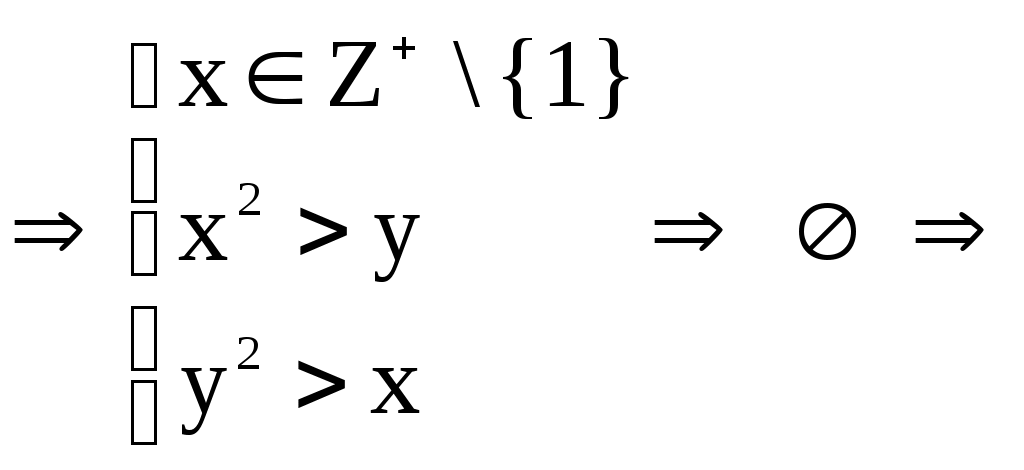P – неантисимметрично.

4) Так как при этом, поэтому P – нетранзи-тивно.







Задание 6.

Является ли алгеброй следующий набор B= ?
Так как константа –3i C\R, +3i C\R, но, подставив в терм, получаем: –3i+3i=0 C\R. Значит, операция сложения не замкнута на множестве C\R. Поэтому набор B= не является алгеброй.







Задание 7.

Постройте подсистему B(X), если B=, X=R
i + i + i +…=in, n

Складывая всевозможные действительные числа, получаем другие действительные числа, то есть операция сложения замкнута на множестве R. Поэтому, подстановка элементов из X в терм ”+” не образует новых элементов.

Таким образом, B(X)= .







Задание 8.

Используя многомодульную арифметику с вектором оснований , вычислить , , , . Каков знак числа ?

, , ,


(43 (mod 5) + 74 (mod 5))(mod 5) = (3 + 4)(mod 5) = 2

(43 (mod 7) + 74 (mod 7))(mod 7) = (1 + 4)(mod 7) = 5

(43 (mod 11) + 74 (mod 11))(mod 11) = (10 + 8)(mod 11) = 7

(43 (mod 2) + 74 (mod 2))(mod 2) = (1 + 0)(mod 2) = 1




(43 (mod 5) – 74 (mod 5))(mod 5) = (3 – 4)(mod 5) = 4

(43 (mod 7) – 74 (mod 7))(mod 7) = (1 – 4)(mod 7) = 4

(43 (mod 11) – 74 (mod 11))(mod 11) = (10 – 8)(mod 11) = 2

(43 (mod 2) – 74 (mod 2))(mod 2) = (1 – 0)(mod 2) = 1




( 43) (mod 5) = 4

( 43) (mod 7) = 3

( 43) (mod 11) = 8

( 43) (mod 2) = 1




(mod 5) = 3 (mod 5) = 3

(mod 7) = 5 (mod 7) = 5

(mod 11) = 2 (mod 11) = 2

(mod 2) = 1 (mod 2) = 1




(mod 5) (mod 5))(mod 5) = (( 2)(mod 5) –

– 4)(mod 5))(mod 5) = (4 – 0)(mod 5) = 4

(mod 7) (mod 7))(mod 7) = (( 6)(mod 7) –

– 3)(mod 7))(mod 7) = (5 – 1)(mod 7) = 4

(mod 11) (mod 11))(mod 11) = (( 6)(mod 11) –

– 7)(mod 11))(mod 11) = (1 – 2)(mod 11) = 10

(mod 2) (mod 2))(mod 2) = (( 1)(mod 2) –

– 1)(mod 2))(mod 2) = (0 – 1)(mod 2) = 1


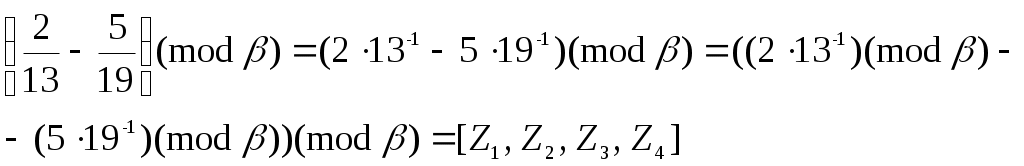
Определим знак числа

Очевидно, что 3

[0, 6, 2, 0] или [6, 2, 0]

Вектор оснований сокращаем до = [7, 11, 2]
Для вычисления вычислим

[3, 9, 1]

Умножим на этот элемент, в результате получим [4, 7, 0]

Таким образом, 4

Вычитая из последнего выражения, получаем [0, 3, 0] или [3, 0]

Вектор оснований = [11, 2]
Вычисляем

[8, 1]

Умножаем на полученный элемент, в результате получаем [2, 0]

Поэтому 2

[0, 0] или [0] для вектора оснований = [2]
Находим

[1]

При умножении на получаем [0]

Отсюда следует, что 0

Поэтому число x – положительное.




Задание 9.

Даны графы и . Найдите , , , . Для графа найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.









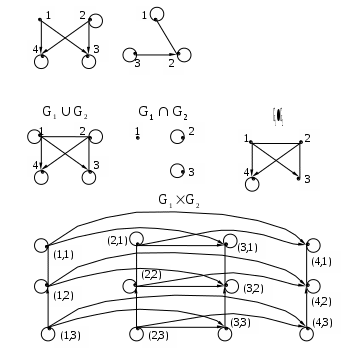
Рассмотрим граф :

Матрица смежности A=





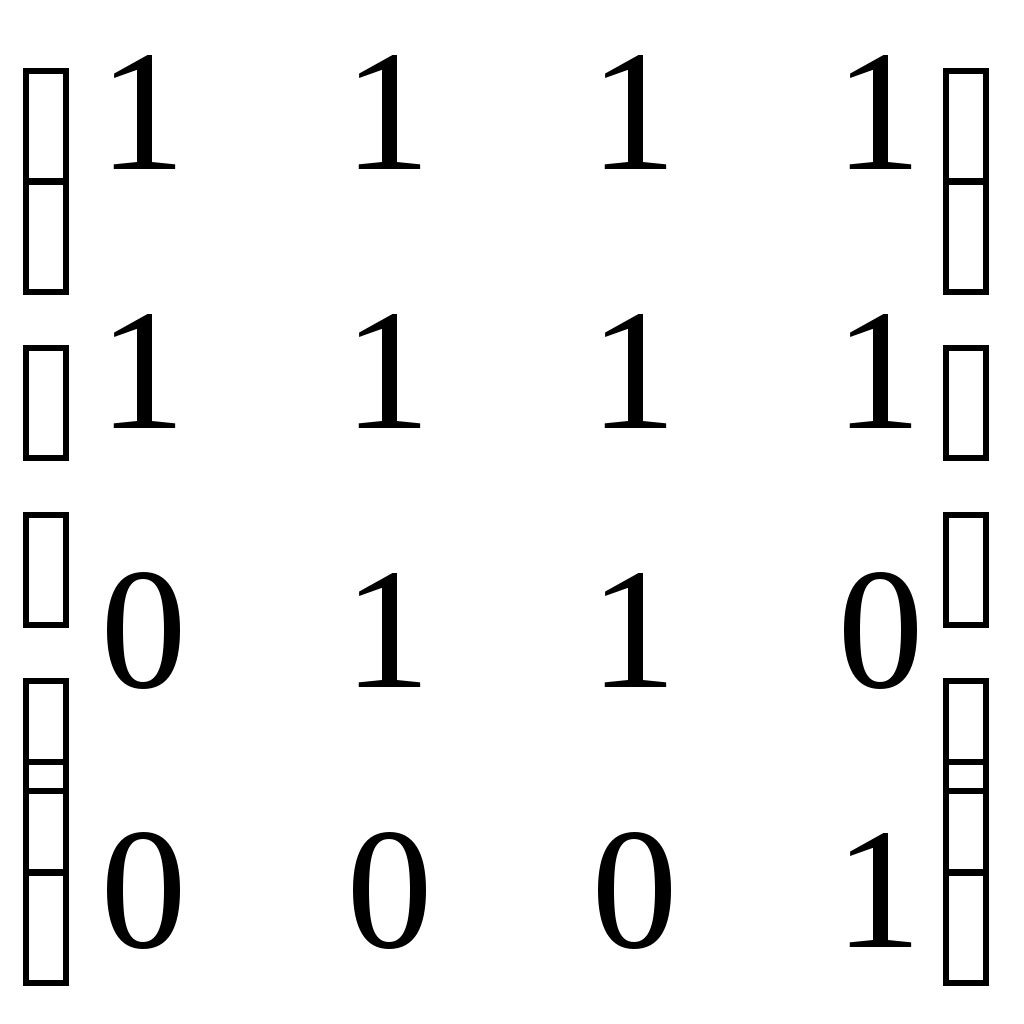
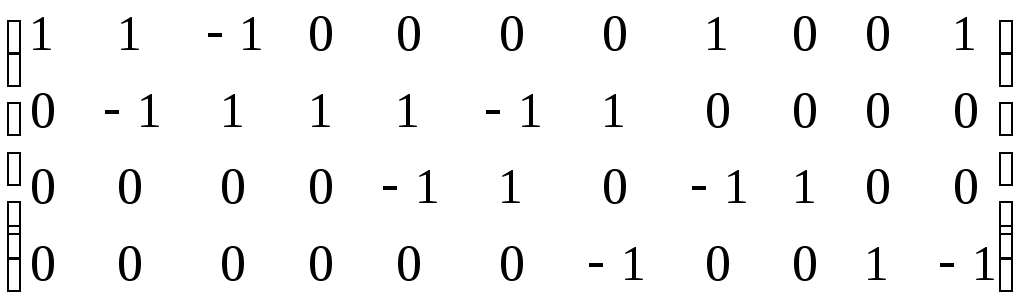– матрица инцидентности
B=E+A+ =

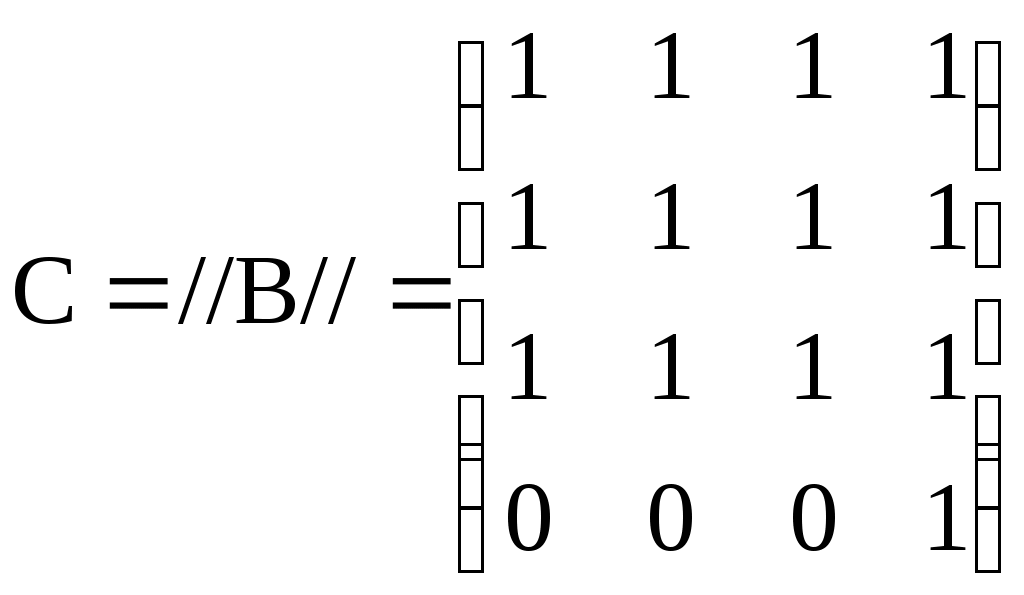
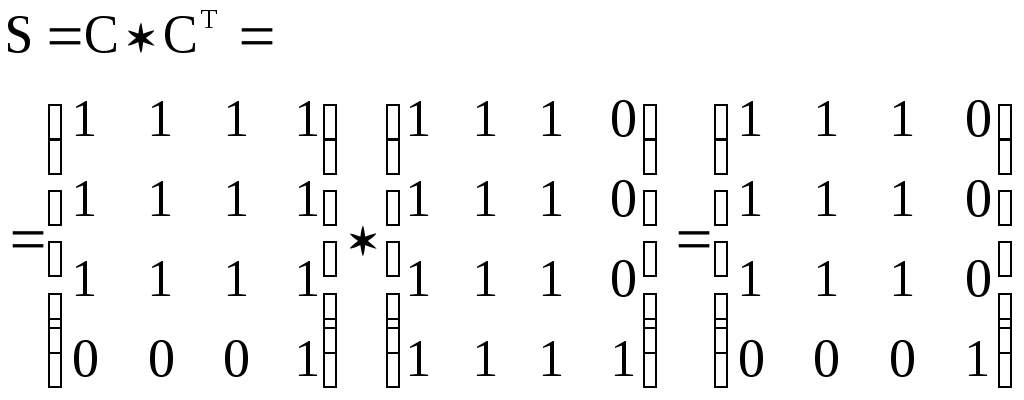– матрица сильных компонент.

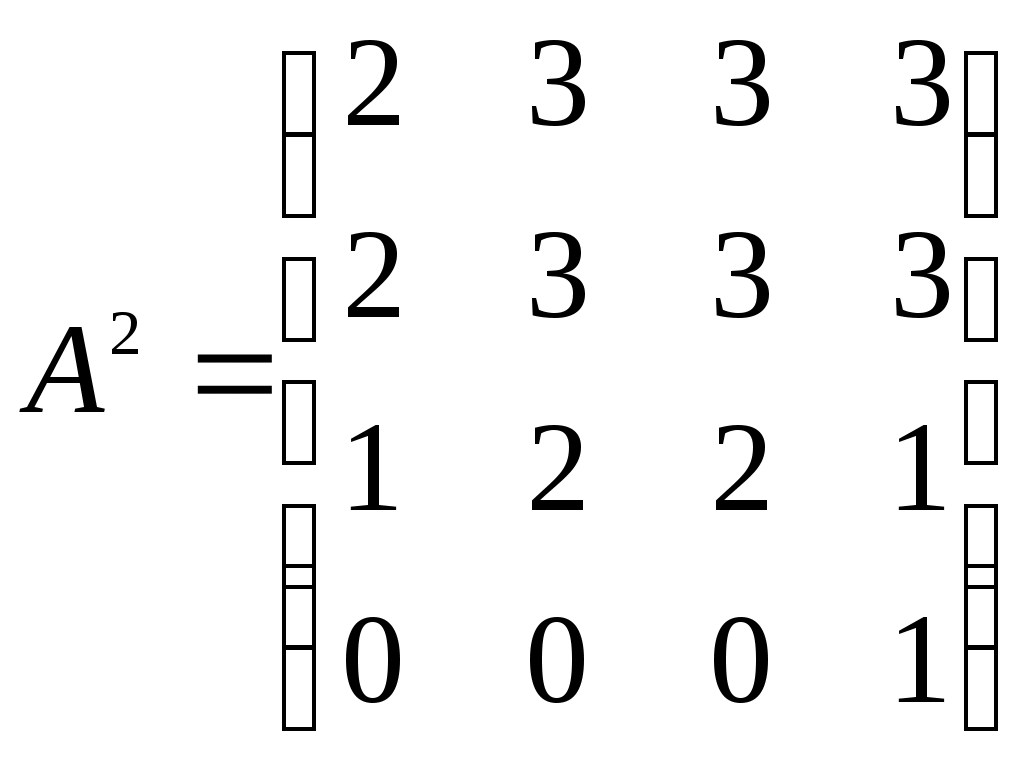– матрица маршрутов длины 2.

Маршруты длины 2, исходящие из вершины 1:

(1;1;1), (1;1;2), (1;1;3), (1;1;4).

(1;2;1), (1;2;2), (1;2;3), (1;2;4).

(1;3;2), (1;3;3), (1;4;4).







Задание 10.

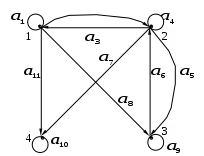
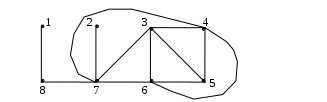
Найдите матрицы фундаментальных циклов, фундаментальных разрезов, радиус и диаметр, минимальное множество покрывающих цепей графа G. Является ли изображенный граф эйлеровым? Является ли изображенный граф планарным?


3


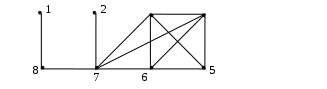
4

Получим остов графа. Для этого удалим из графа 12–8+1=5 ребер.

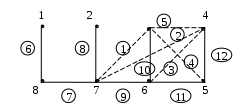
3

Матрица фундаментальных циклов:



C=

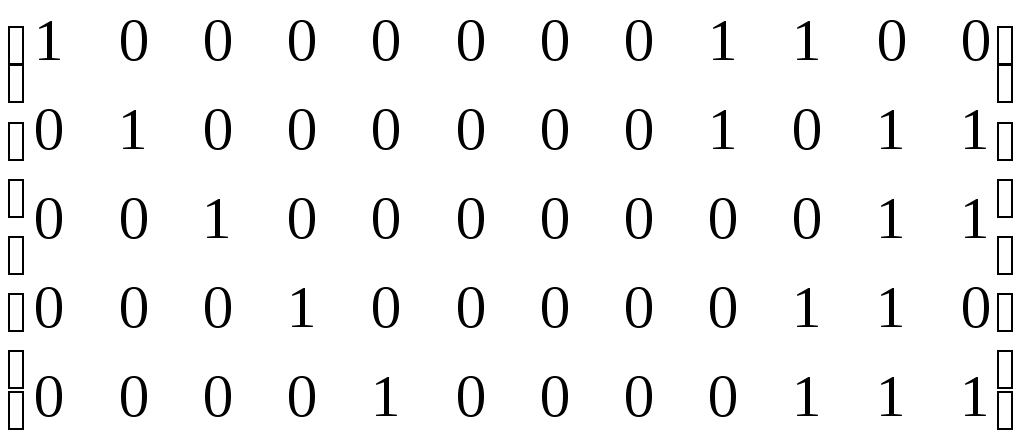
Матрица фундаментальных разрезов:



K=

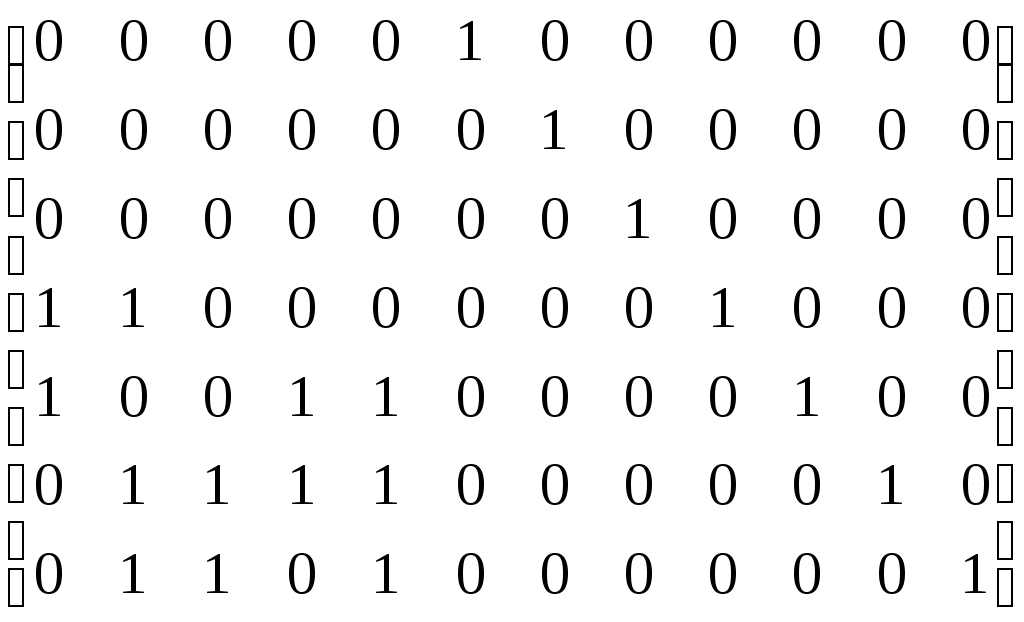
Диаметр d(G)=4

Радиус r(G)=2
Минимальное множество покрывающих цепей графа – 2.

2,7,3,4,6,5,3,6,7,4,5

1,8,7
Граф не является эйлеровым, так как степени не всех его вершин четные.

Граф планарный.





Задание 11.

Составьте таблицы истинности формул:
1)

x	y
0	0	1	0	0	1
0	1	0	1	1	0
1	0	1	1	0	0
1	1	0	1	1	1

2)

x	y	z
0	0	0	1	0	1	1	0	0
0	0	1	1	0	0	1	1	1
0	1	0	1	0	1	0	1	1
0	1	1	1	0	0	0	0	0
1	0	0	1	0	1	1	0	1
1	0	1	1	0	0	1	1	1
1	1	0	0	1	0	0	0	1
1	1	1	0	1	0	0	0	1

Задание 12.
Проверьте двумя способами, будут ли эквивалентны следующие формулы

=x (y z) и =(x y) (x z)

а) составлением таблиц истинности

б) приведением формул к СДНФ или СКНФ с помощью эквивалентных преобразований.
а)

x	y	z	y z		x y	x z
0	0	0	1	1	1	1	0
0	0	1	0	1	1	1	0
0	1	0	0	1	1	1	0
0	1	1	0	1	1	1	0
1	0	0	1	1	0	0	1
1	0	1	0	0	0	1	0
1	1	0	0	0	1	0	0
1	1	1	0	0	1	1	0

Так как столбцы и не совпадают, то формулы неэквивалентны.

б)




Так как СДНФ не совпадают, то формулы неэквивалентны.







Задание 13.

С помощью эквивалентных преобразований приведите формулу к ДНФ, КНФ, СДНФ, СКНФ. Постройте полином Жегалкина.








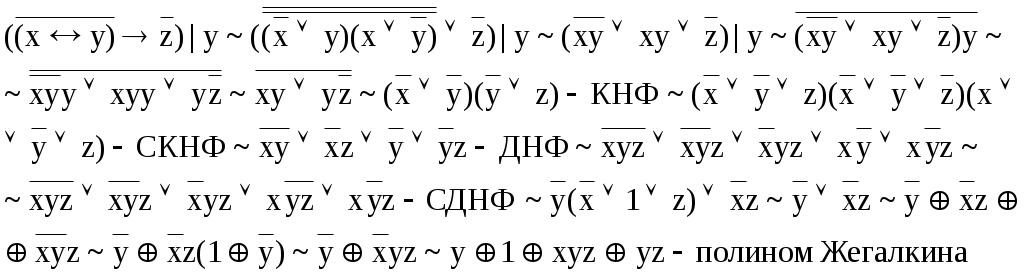
Задание 14.

Найдите сокращенную, все тупиковые и минимальные ДНФ булевой функции двумя способами:

а) методом Квайна б) с помощью карт Карно

Каким классам Поста принадлежит эта функция?


а)

x	y	z
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

	*	*
		*		*
			*	*

– тупиковая и минимальная ДНФ.
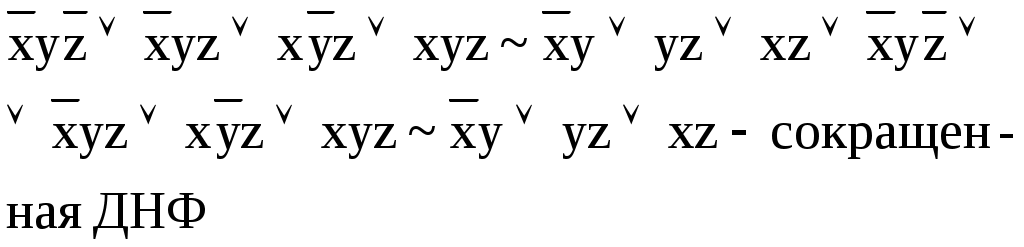
б)







– тупиковая и минимальная ДНФ.

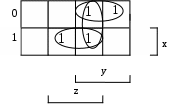
1) функция сохраняет ноль

2) функция сохраняет единицу

3) – функция несамодвойственная.

4 ) – функция немонотонная






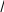Задание 15.

С помощью карт Карно найдите сокращенную, все тупиковые и минимальные ДНФ и КНФ булевой функции , заданной вектором своих значений.

(0011 1101 0010 1100)

x	y	z	v
0	0	0	0	0
0	0	0	1	0
0	0	1	0	1
0	0	1	1	1
0	1	0	0	1
0	1	0	1	1
0	1	1	0	0
0	1	1	1	1
1	0	0	0	0
1	0	0	1	0
1	0	1	0	1
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	0
1	1	1	1	0

– сокращенная ДНФ.

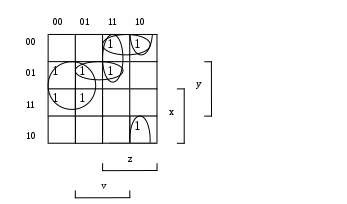
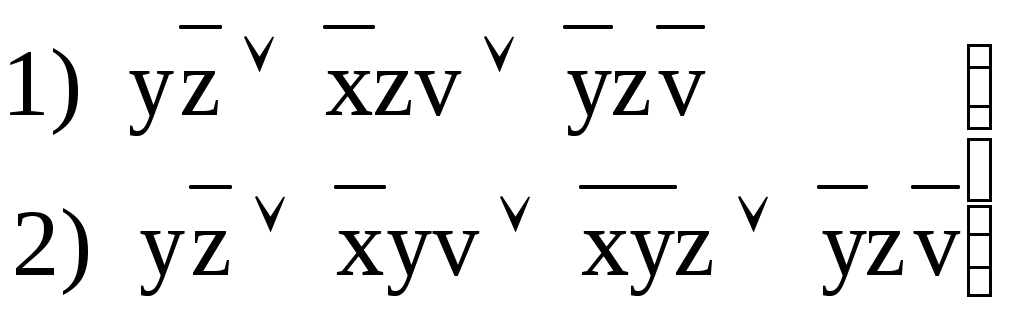тупиковые ДНФ.

1) – минимальная ДНФ.


– сокращенная КНФ.

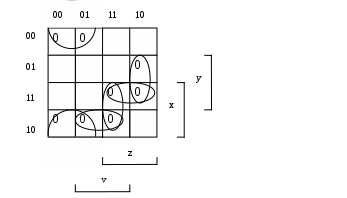
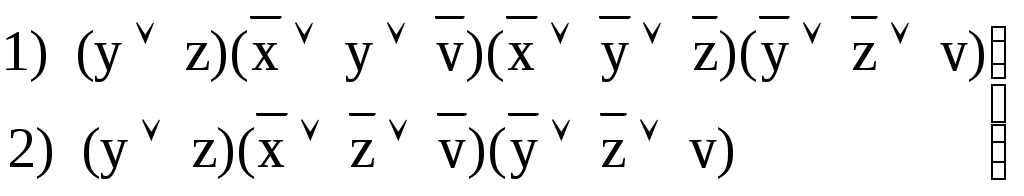– тупиковая КНФ.

2) – минимальная КНФ.







Задание 16.

Является ли полной система функций

  1   2

---

J= ? Образует ли она базис?


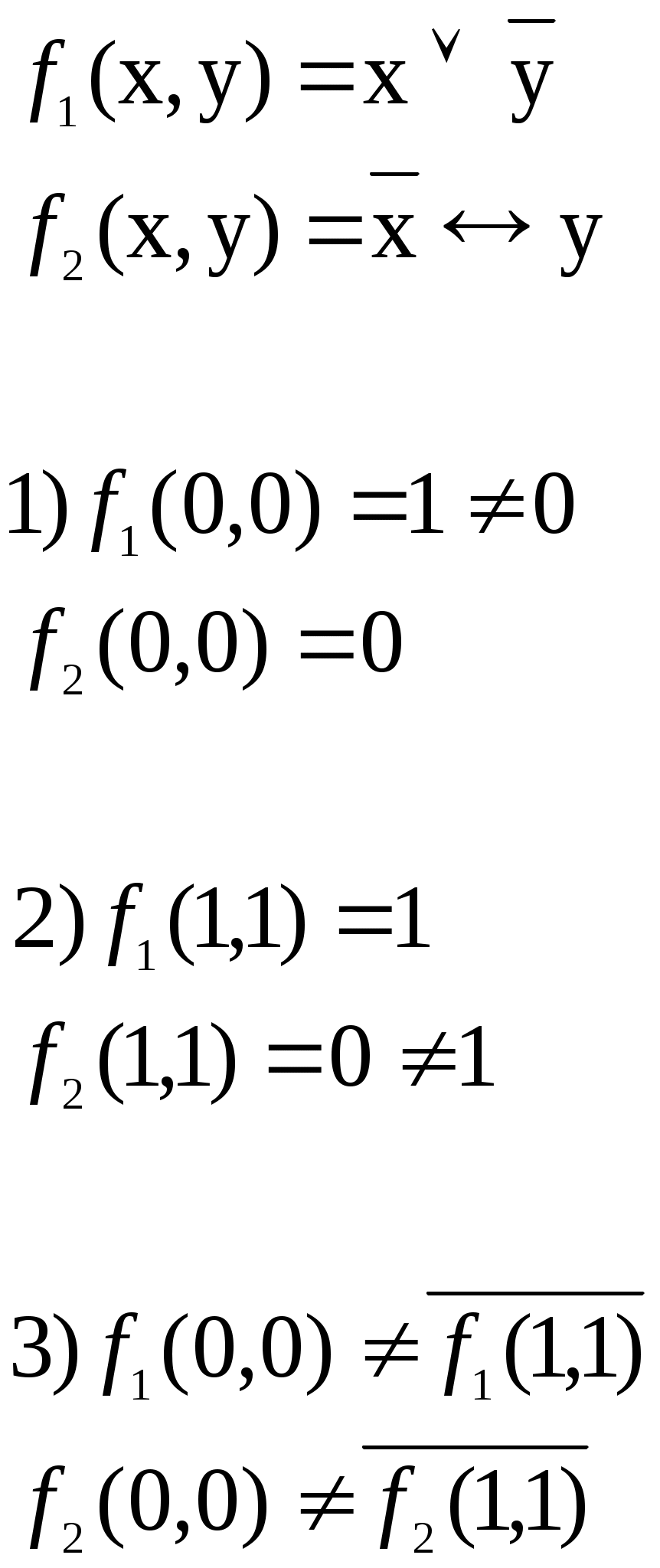
функция не сохраняет ноль

функция сохраняет ноль

функция сохраняет единицу

функция не сохраняет единицу

функция несамодвойственная

функция несамодвойственная

4 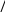) 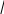функция немонотонная

функция немонотонная




- функция нелинейная, т. к. полином Жегалкина нелинейный.

Функция	Классы
	P0	P1	S	M	L
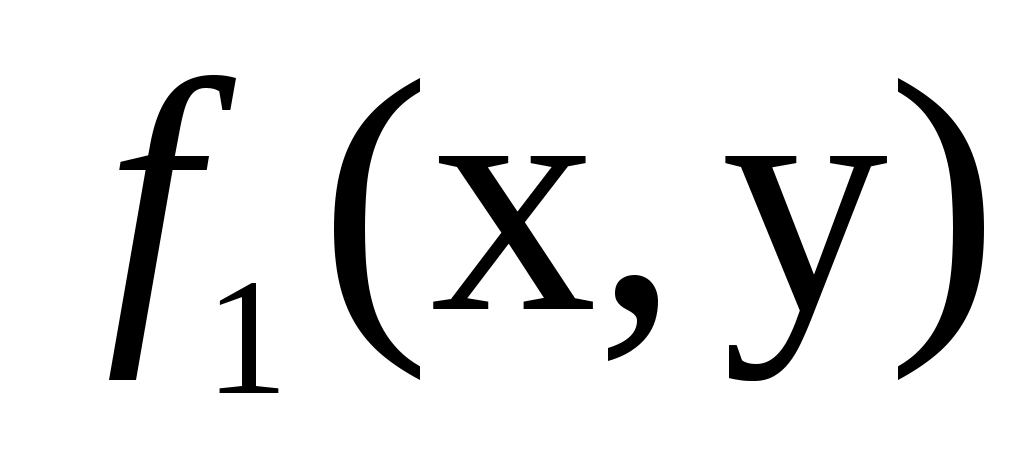
	нет	да	нет	нет	нет
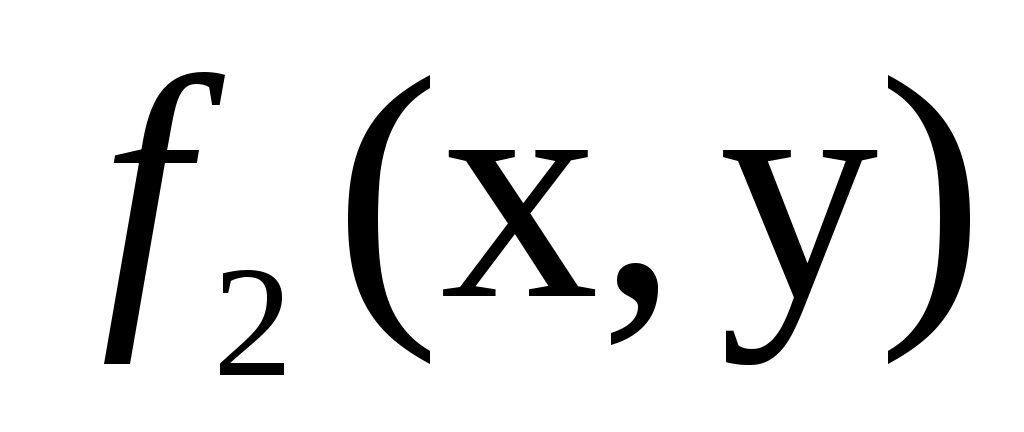
	да	нет	нет	нет	да

---

Так как для каждого из классов в системе Jнайдется функция, не принадлежащая этому классу, то система булевых функций J полная. Удаление любой из функций делает ее неполной, значит, она образует базис.







Задание 17.

С помощью алгебры логики проверьте истинность соотношения

для любых множеств A, B, C. Если соотношение неверно, постройте контрпример.

x	y	z
0	0	0	1	0	1	0	1	0	0
0	0	1	0	0	1	0	1	0	0
0	1	0	1	1	0	0	0	0	0
0	1	1	0	0	1	0	0	0	0
1	0	0	1	0	1	1	1	1	1
1	0	1	0	0	1	1	1	1	0
1	1	0	1	1	0	0	0	0	0
1	1	1	0	0	1	1	0	0	0

---

Смотрите также файлы

• Дисциплина Экологические основы природопользования Практическое занятие 2 Обучающийся Устинова Анна Сергеевна Преподаватель Чащинова Анна Вадимовна Задание 1.rtf

• Управление распределительными каналами предприятия.docx

• Охранные системы безопасности.docx

• Интерактивная сторона общения понятие, примеры из жизни, виды.docx

• Психологические особенности детей дошкольного возраста.docx