ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 1091
Скачиваний: 24
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, (7.1)
где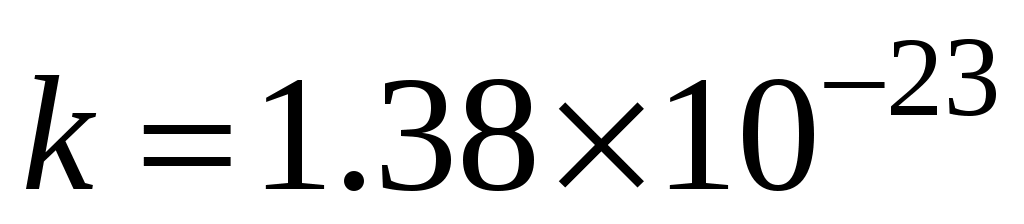 Дж/К – постоянная Больцмана,
Дж/К – постоянная Больцмана, 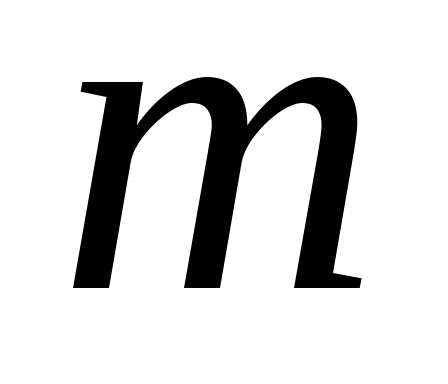 - масса молекулы. Более удобно работать с безразмерной скоростью
- масса молекулы. Более удобно работать с безразмерной скоростью 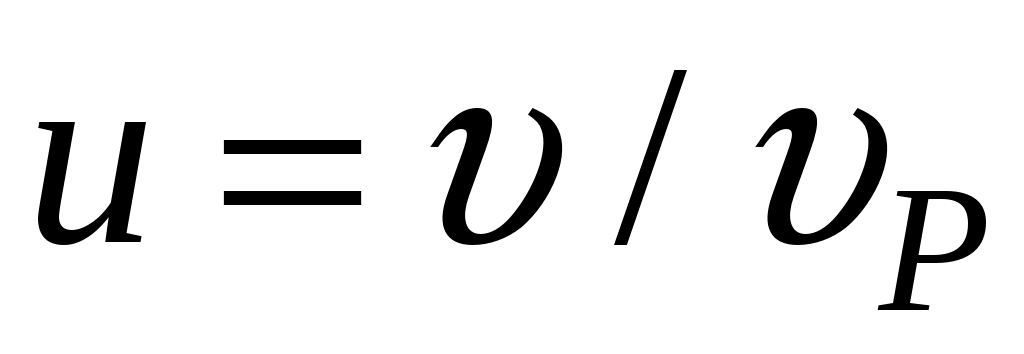 , где,
, где, 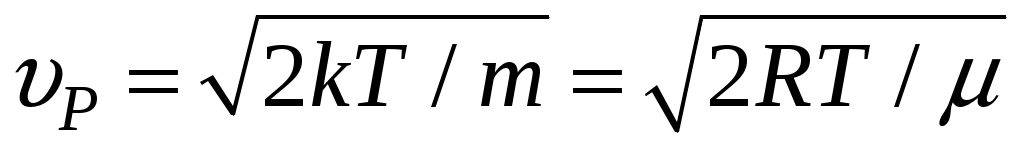 - наиболее вероятная скорость,
- наиболее вероятная скорость, 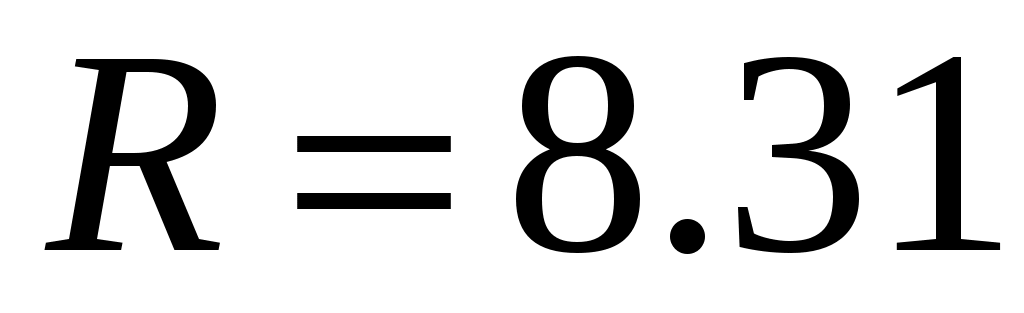 Дж/мольК,
Дж/мольК,  - молярная масса газа. Тогда распределение Максвелла принимает простой вид
- молярная масса газа. Тогда распределение Максвелла принимает простой вид
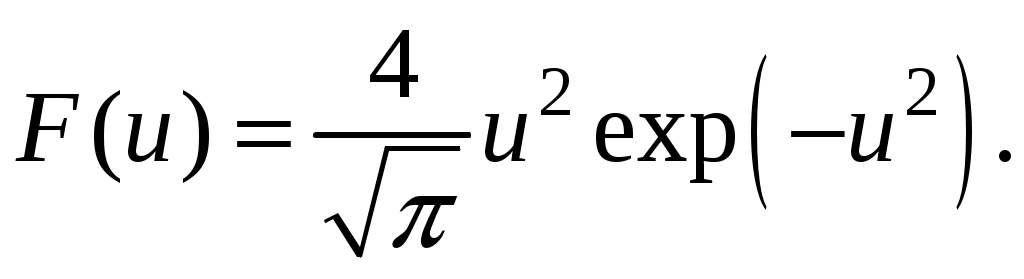 (7.2)
(7.2)
Решение
Кинетическая энергия молекулы состоит из поступательной и вращательной энергий, суммарное значение которых равно 1 эВ. Атом гелия имеет 3 степени свободы. По закону равнораспределения на одну степень свободы молекулы приходится средняя энергия
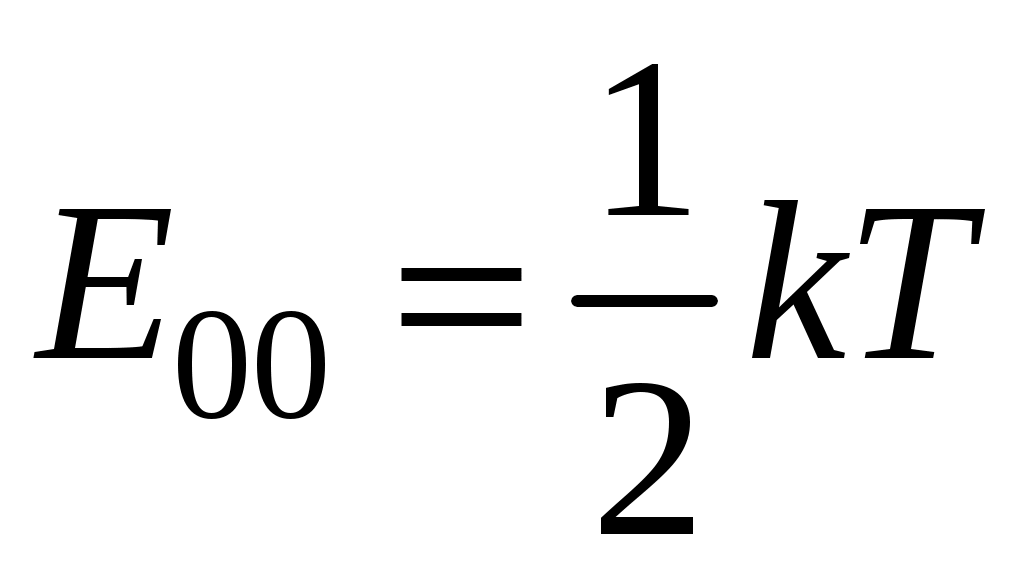 (7.3)
(7.3)
Поэтому для атомов гелия мы имеем
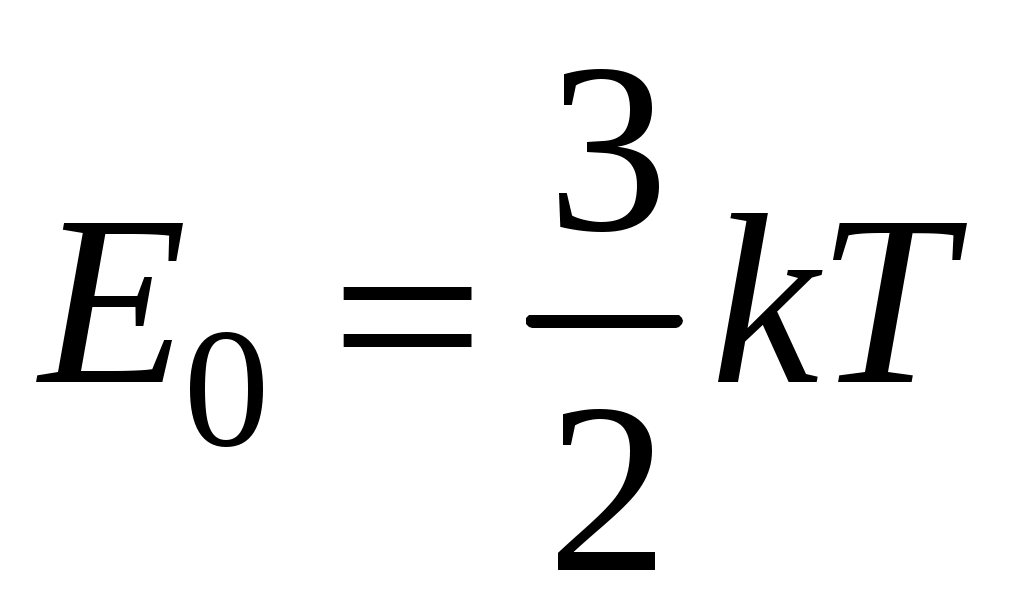 (7.4)
(7.4)
тогда температура, при которой энергия атомов гелия равна 1 эВ будет определяться из следующей цепочки
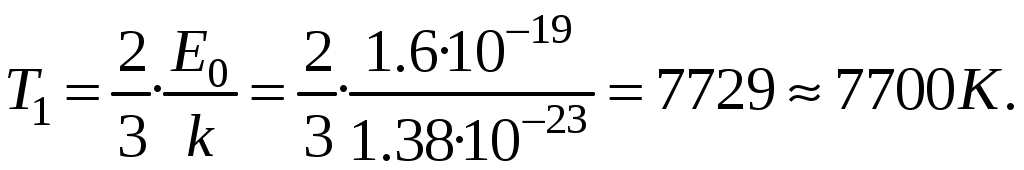
Относительная доля молекул идеального газа, чьи скорости лежат в диапазоне от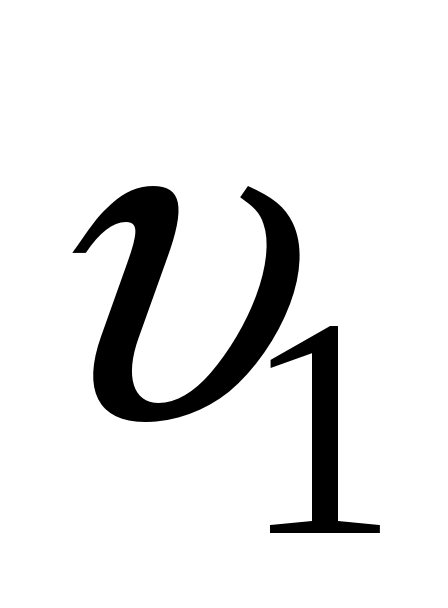 до
до 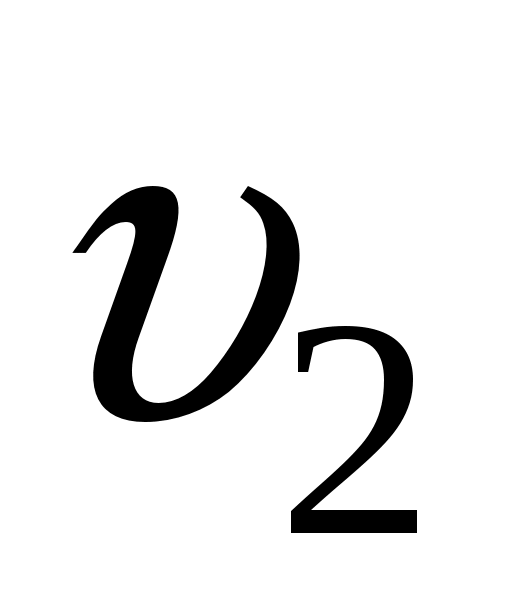 из распределения молекул идеального газа по скоростям (распределение Максвелла), заданного (7.1).
из распределения молекул идеального газа по скоростям (распределение Максвелла), заданного (7.1).
Для того, чтобы найти долю частиц, у которых скорости находятся в диапазоне от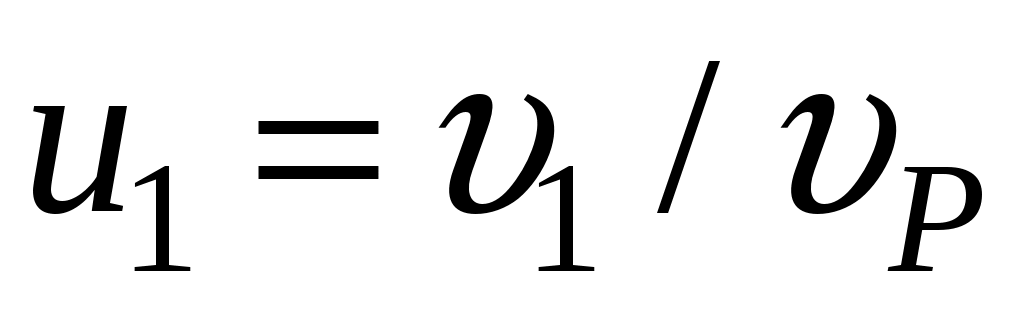 до
до 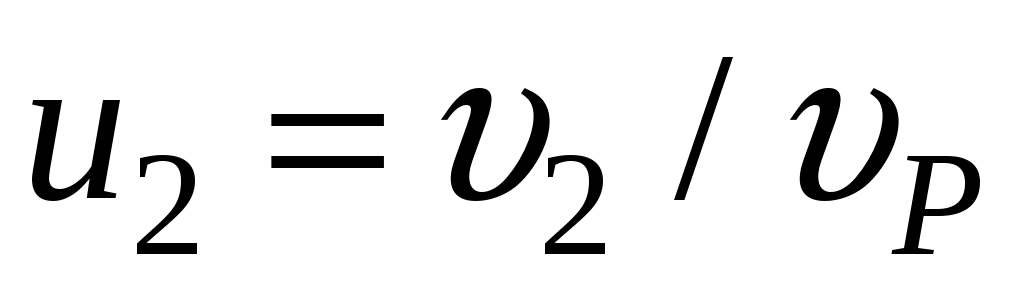 , необходимо вычислить интеграл
, необходимо вычислить интеграл
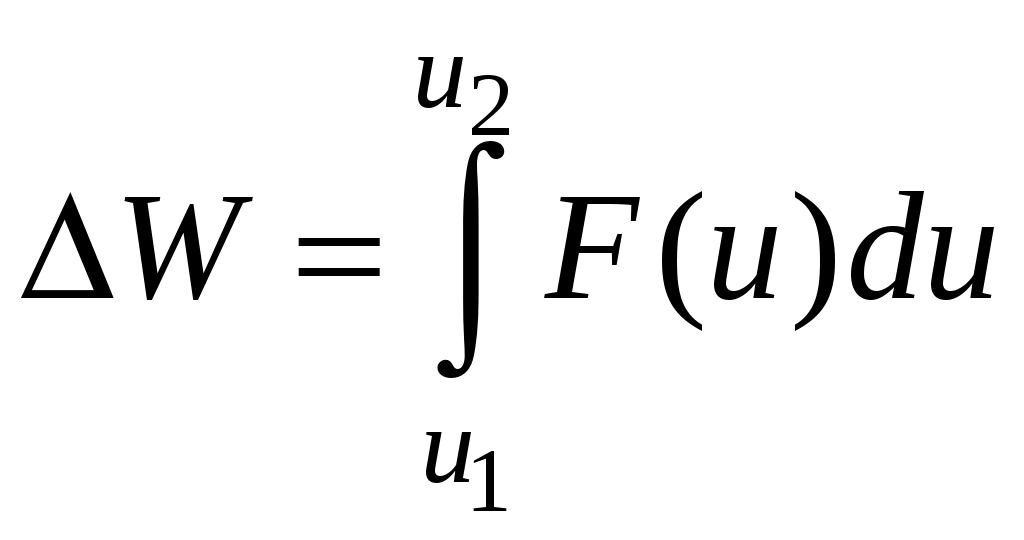 (7.5)
(7.5)
Вычислим скорости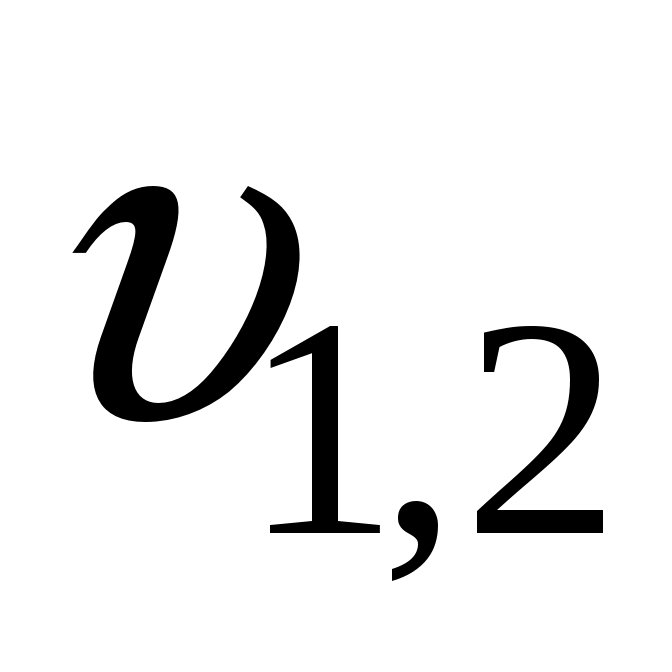
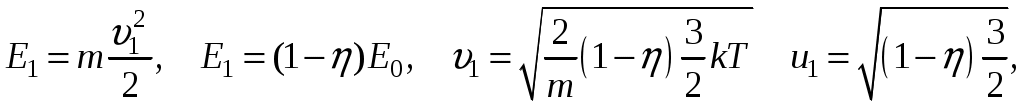 (7.6)
(7.6)
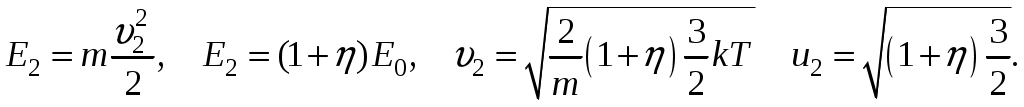 (7.7)
(7.7)
Итак, скорости равны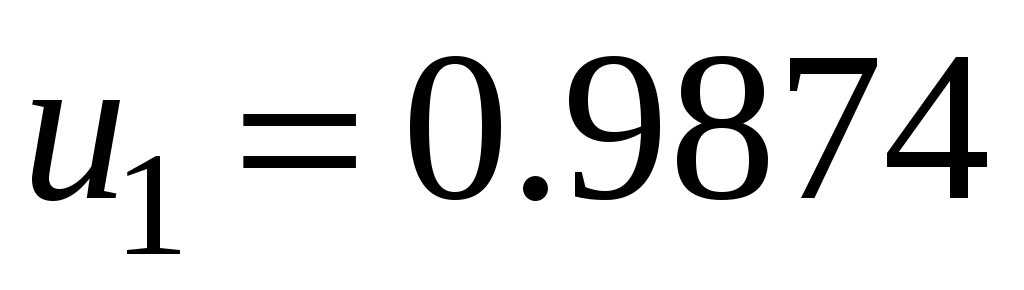 ,
, 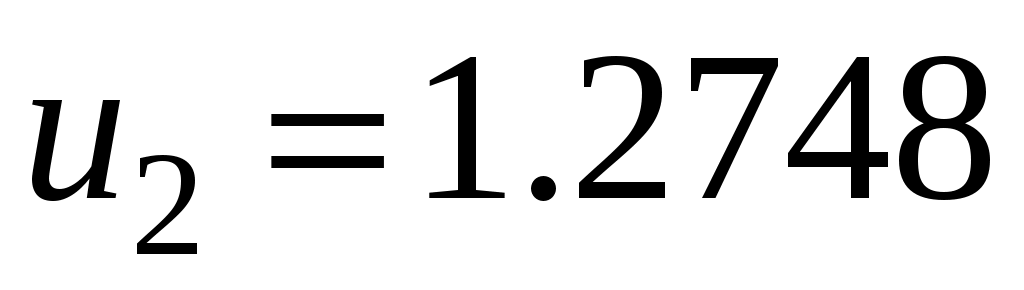 . Для вычисления интеграла (7.5) используем простейшую квадратурную формулу прямоугольников
. Для вычисления интеграла (7.5) используем простейшую квадратурную формулу прямоугольников
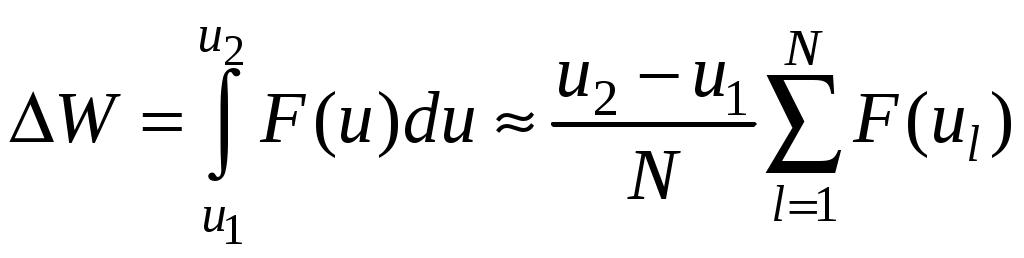 (7.8)
(7.8)
реализованную в виде псевдокода
begin\\
q=1.6e-19;\\
k=1.38e-23;\\
E0=1*q;\\
i=3;\\
T1=2*E0/3/k\\
nu=0.25\\
u1=sqrt(1.3*(1-nu))\\
u2=sqrt(1.3*(1+nu))\\
N=500\\
du=(u2-u1)/N;\\
sums=0\\
for j=1:N\\
u=u1+j*du;\\
sums=sums+u*u*exp(-u*u);\\
end\\
DW=4*du*sums/sqrt(pi)\\
% Распределение молекул газа по скоростям
v1=0\\
v2=4\\
N=100\\
dv=(v2-v1)/N;\\
sums=0\\
for j=1:N\\
u=v1+j*dv;\\
v(j)=u;\\
f(j)=4*u*u*exp(-u*u)/sqrt(pi);\\
sums=sums+f(j);\\
end\\
DW0=dv*sums\\
end\\
Выполняя расчет (8.8), получаем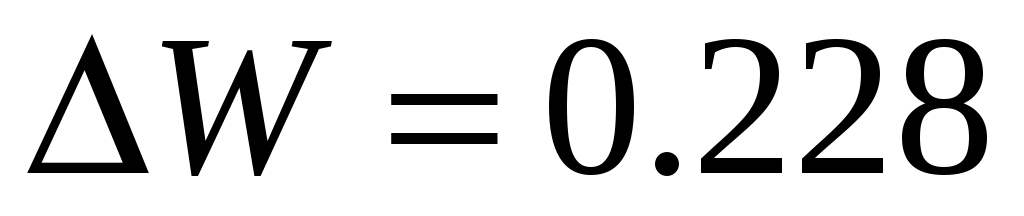 .
.
Построим график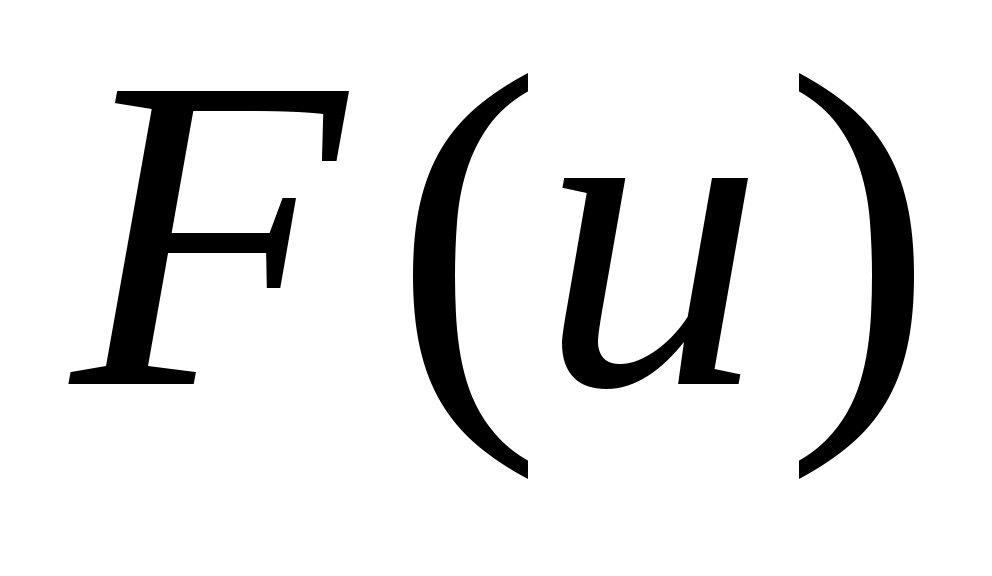
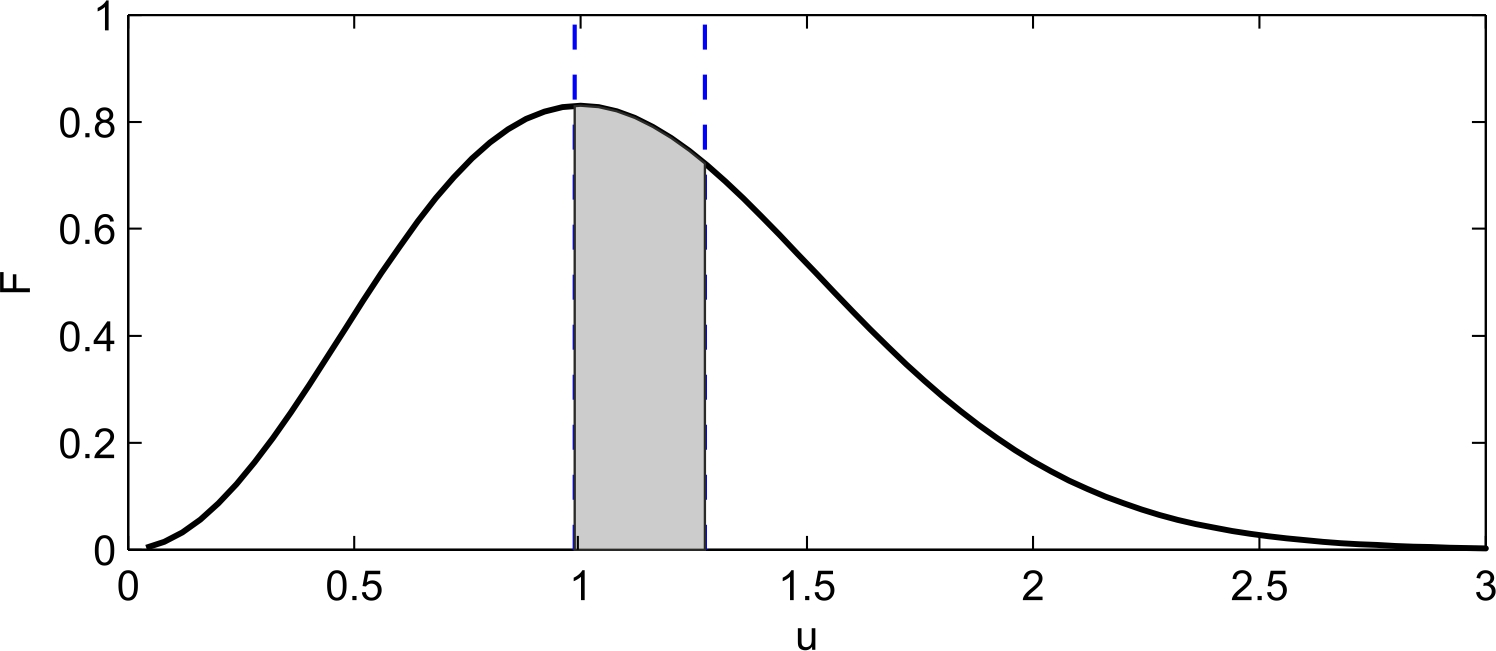
Рис.7.1.Распределение молекул газа по скоростям
Анализ решения
Оценивая «на глаз» заштрихованную площадь и полученное численное значение вероятности , убеждаемся, что в грубом приближении заштрихованная площадь занимает примерно пятую часть всей площади под кривой плотности распределения
, убеждаемся, что в грубом приближении заштрихованная площадь занимает примерно пятую часть всей площади под кривой плотности распределения 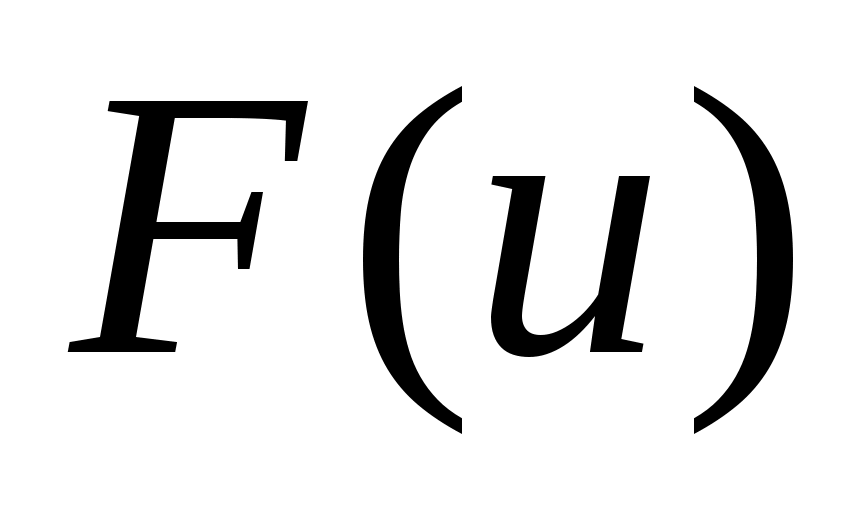 , соответственно, численное решение согласуется с графическим представлением. Более точно, площадь области, выделенной на рис.1, равна 0.228.
, соответственно, численное решение согласуется с графическим представлением. Более точно, площадь области, выделенной на рис.1, равна 0.228.
Ответ: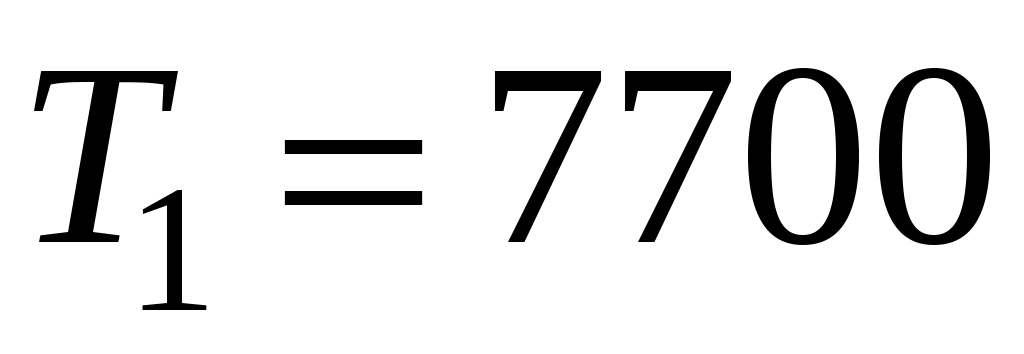 К,
К, 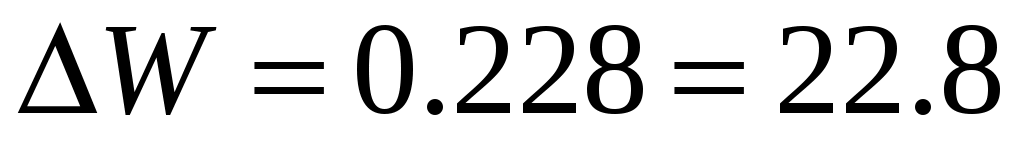 %.
%.
***
7.1. Энергию атомных и субатомных частиц часто измеряют в электрон-вольтах, 1 эВ = 1.6×10-19 Дж. Найти, при какой температуре средняя кинетическая энергия молекулы азота равна 1 эВ. Определить, при какой температуре 25% всех молекул имеют кинетическую энергию, превышающую 1 эВ. Постройте график зависимости
 (см. пример 7.1), отметьте (заштрихуйте) искомую область.
(см. пример 7.1), отметьте (заштрихуйте) искомую область.
7.2. Азот массой 12 г находится в закрытом сосуде при температуре 300 К. Какое количество теплоты необходимо передать азоту, чтобы средняя квадратичная скорость молекул возросла в 2 раза? Привести поясняющий рисунок и указать основные параметры.
7.3. Газ, состоящий из жестких двухатомных молекул, находится при температуре 300 К. Вычислить среднюю квадратичную угловую скорость вращения молекулы, если ее момент инерции равен 2.1 10-46 кг м2. Привести поясняющий рисунок и указать основные параметры.
7.4. В вакуумном диоде электроны, эмитируемые накаленным катодом, попадают в задерживающее поле анода. До анода доходят лишь достаточно быстрые электроны. Считая, что тепловые скорости эмитируемых (вышедших из катода) электронов распределены по закону Максвелла с температурой 1150 К, определить долю электронов, преодолевающих задерживающий потенциал а) 0.2 В, б) 0.4 В. Катодом является тонкая прямолинейная нить, натянутая по оси цилиндрического анода. Привести поясняющий рисунок и указать основные параметры.
7.5. Найти отношение числа молекул водорода, скорости которых лежат в пределах от 3000 м/с до 3050 м/с, к числу молекул, имеющих скорости в пределах от 1550 м/с до 1600 м/с, если температура водорода 573 К. Постройте график зависимости (см. пример 7.1), отметьте (заштрихуйте) искомые области, сравните их между собой и результатами расчетов.
(см. пример 7.1), отметьте (заштрихуйте) искомые области, сравните их между собой и результатами расчетов.
7.6. Какая часть молекул кислорода обладает скоростями, отличающимися от наивероятнейшей не больше чем на 25 м/с при температурах 273 К и 573 К? Постройте график зависимости (см. пример 7.1), отметьте (заштрихуйте) искомые области, сравните их между собой и результатами расчетов.
(см. пример 7.1), отметьте (заштрихуйте) искомые области, сравните их между собой и результатами расчетов.
7.7. Определить отношение числа молекул водорода, обладающих скоростями в интервале от 2500 м/с до 2600 м/с, к числу молекул, обладающих скоростями от 1500 м/с до 1600 м/с, если температура водорода 273 К. Постройте график зависимости (см. пример 7.1), отметьте (заштрихуйте) искомые области, сравните их между собой и результатами расчетов.
(см. пример 7.1), отметьте (заштрихуйте) искомые области, сравните их между собой и результатами расчетов.
7.8. Найти полное число молекул и их вес в столбе атмосферы с основанием 1 см
2 , если концентрация молекул у земли n0 = 2.691019 см-3 при Т = 273 К, = 0.029 кг/моль. Привести поясняющий рисунок и указать основные параметры.
7.9. Оценить порядок величины полного числа молекул в атмосфере Земли, считая, что плотность молекул описывается барометрической формулой при постоянной температуре Т=273 К, а радиус Земли равен 6370 км. Привести поясняющий рисунок и указать основные параметры.
7 .10. (См.[3]) Дымовая труба высотой 150 м выпускает дым при температуре
.10. (См.[3]) Дымовая труба высотой 150 м выпускает дым при температуре 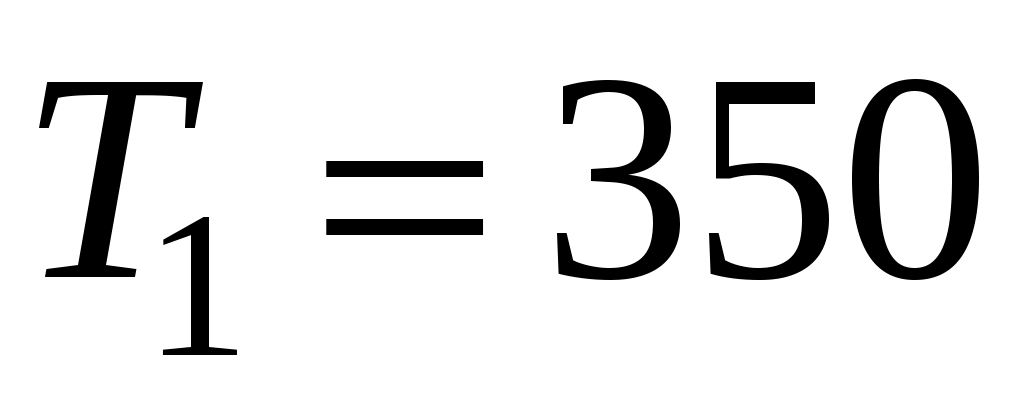 К. Определить перепад давления на входе в трубу, обеспечивающий тягу. Температура и давление наружного воздуха
К. Определить перепад давления на входе в трубу, обеспечивающий тягу. Температура и давление наружного воздуха 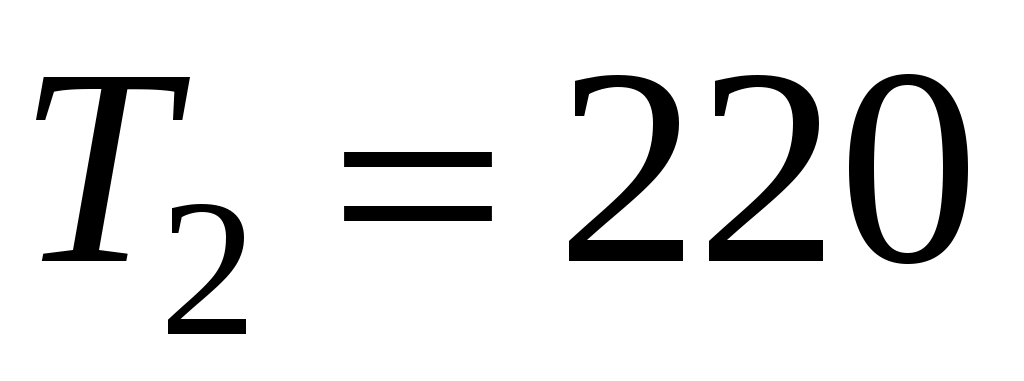 К и
К и 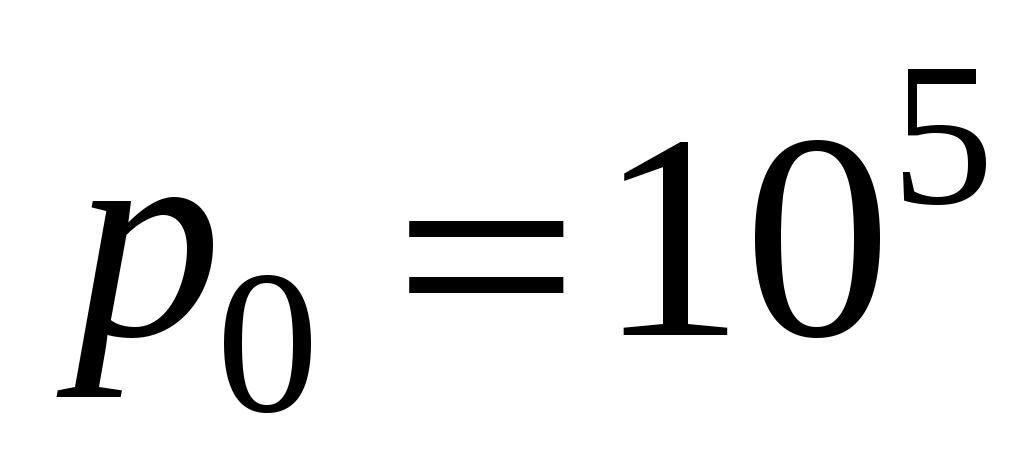 Па, соответственно. Построить график зависимости перепада давления
Па, соответственно. Построить график зависимости перепада давления 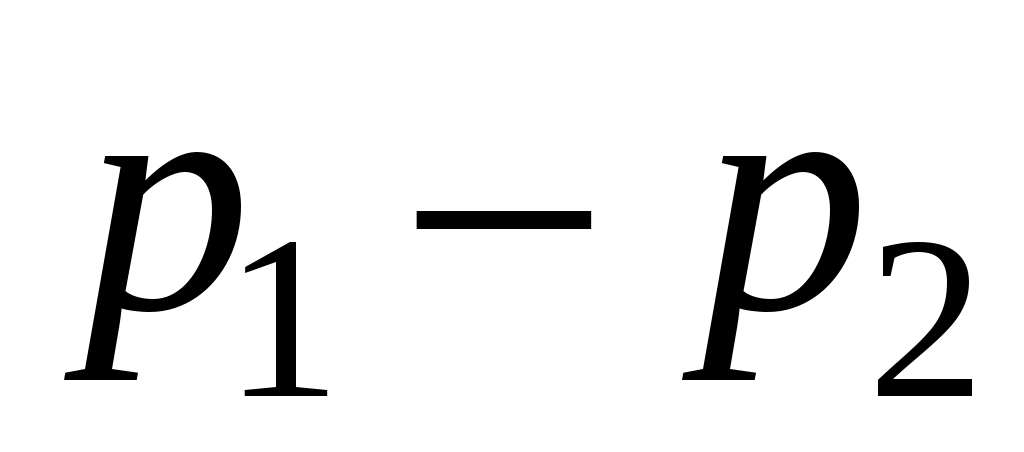 от температуры
от температуры 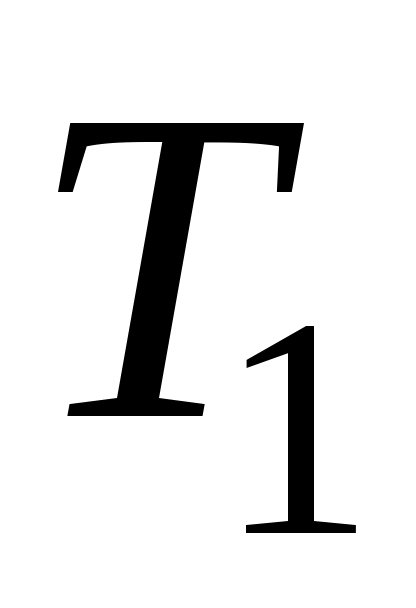 газов в трубе при фиксированной температуры и давлении наружного воздуха. Привести поясняющий рисунок и указать основные параметры.
газов в трубе при фиксированной температуры и давлении наружного воздуха. Привести поясняющий рисунок и указать основные параметры.
7.11. Для определения числа Авогадро Перрен измерял распределение по высоте шарообразных частиц гуммигута, взвешенных в воде. Он нашел , что отношение количества частиц в слоях, отстоящих друг от друга на расстоянии 30 мкм, равно 2.08. Плотность частиц 1194 кг/м3, воды 1000 кг/м3. Радиусы частиц 0.212 мкм. На основании этих данных вычислите число Авогадро. Температура воды 18о С. Привести поясняющий рисунок и указать основные параметры.
7.12. Вычислить наиболее вероятную энергию молекул в идеальном газе и показать, что эта энергия не равна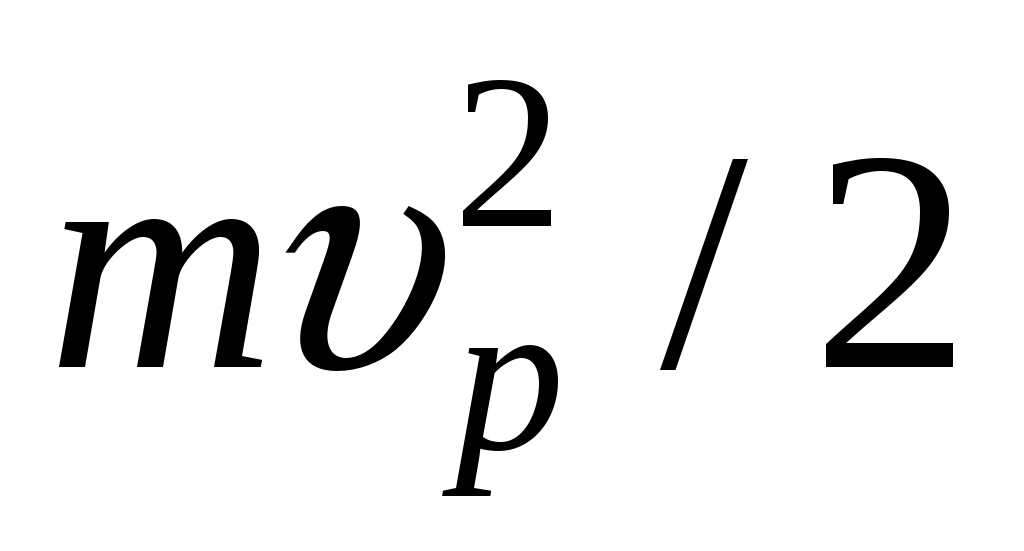 . Привести поясняющий рисунок и указать основные параметры.
. Привести поясняющий рисунок и указать основные параметры.
8. Явления переноса
Пример 8.1 Теплопроводность. Сколько теплоты протекает через окно с двойной рамой за один час, если окно имеет размеры 0.76х1.12 м? Толщина слоя воздуха между рамами 0.16 м, температура наружнего воздуха –350 С, а внутри дома 200 С.
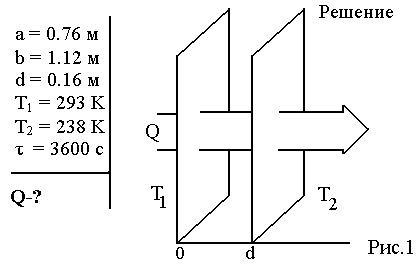
Теплопотери через окно можно вычислить на основе эмпирического закона Фурье (см., например, [7] с.86)
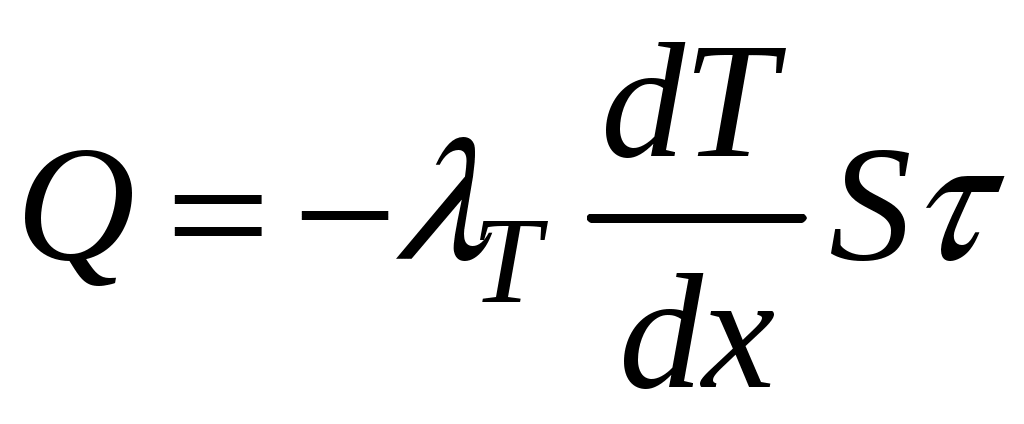 (8.1)
(8.1)
Здесь Q - количество теплоты, переданное через окно, площадью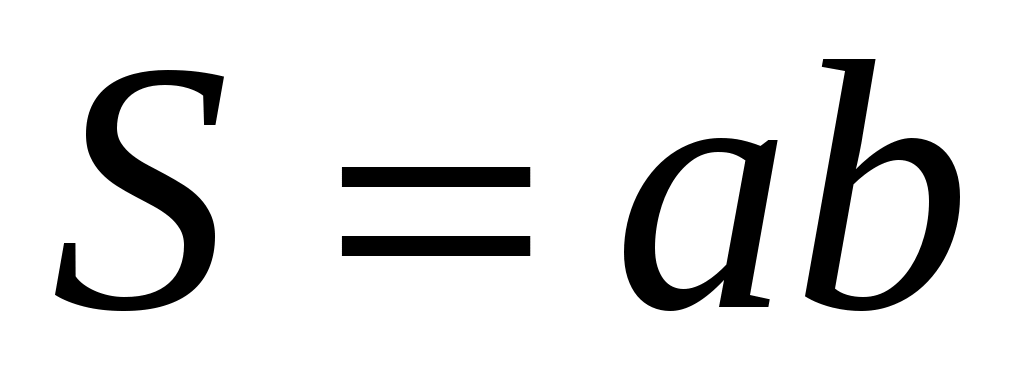 . В качестве разумного предположения примем, что градиент температуры является постоянной величиной, тогда
. В качестве разумного предположения примем, что градиент температуры является постоянной величиной, тогда
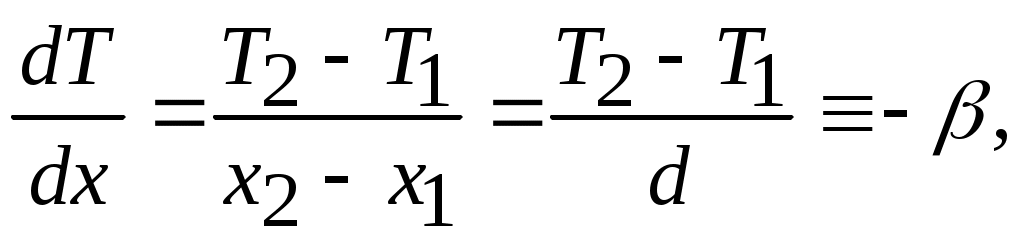 (8.2)
(8.2)
где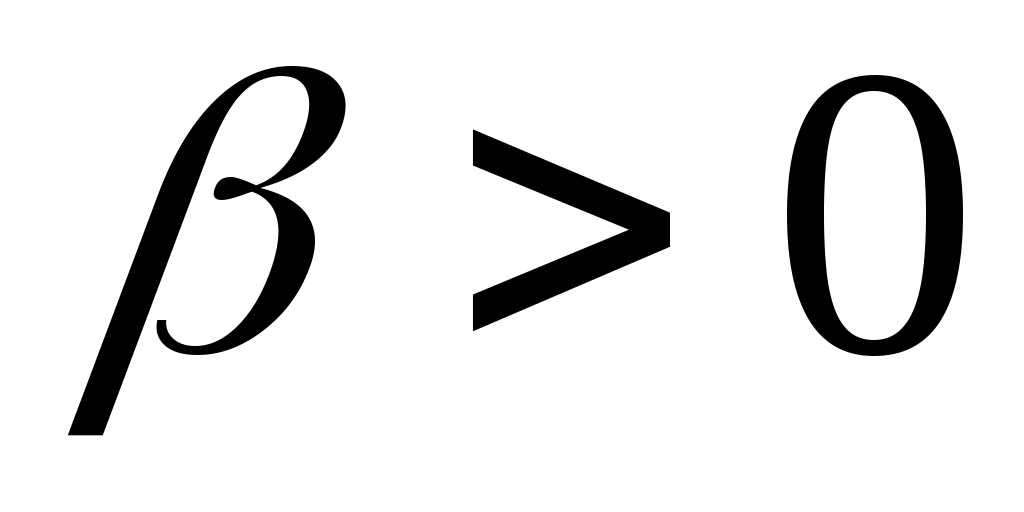 . На самом деле (9.2) есть выражение для среднего градиента температуры. Он в принципе не может быть постоянным вдоль оси X, поскольку коэффициент теплопроводности зависит от температуры, а поток тепла, разумеется, одинаков в любом поперечном сечении. Таким образом,
. На самом деле (9.2) есть выражение для среднего градиента температуры. Он в принципе не может быть постоянным вдоль оси X, поскольку коэффициент теплопроводности зависит от температуры, а поток тепла, разумеется, одинаков в любом поперечном сечении. Таким образом, 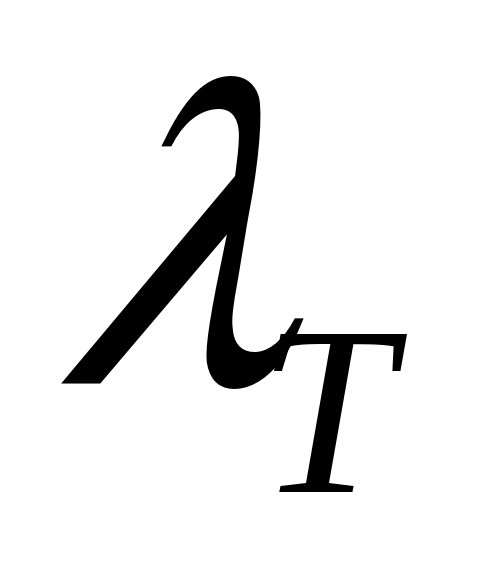 также должен быть усреднен.
также должен быть усреднен.
Теплопроводность воздуха является одной из важнейших характеристик, используемых при проектировании различных сооружений, в двигателестроении, в химической технологии и т.п., поэтому имеются обширные таблицы этой величины, измеренной при различных давлениях и температурах. Воспользуемся опытными данными, взятыми из справочника [8] (с. 345) и приведенными в Приложении. Как видно из рис.А.1 зависимость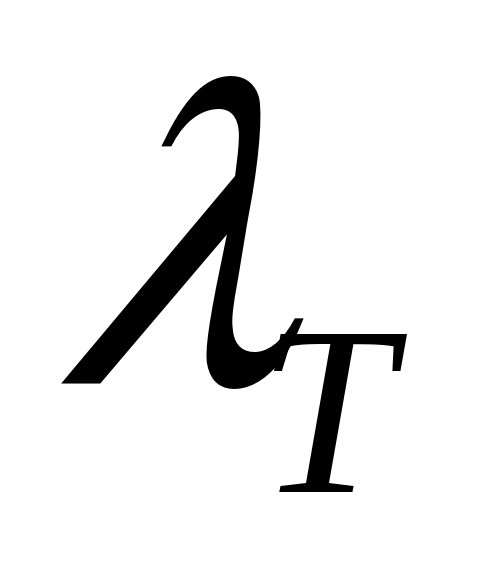 от температуры хорошо аппроксимируется линейной функцией
от температуры хорошо аппроксимируется линейной функцией
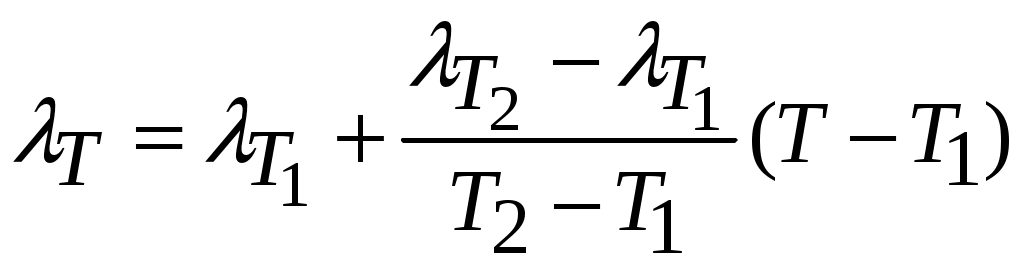 (8.3)
(8.3)
где значения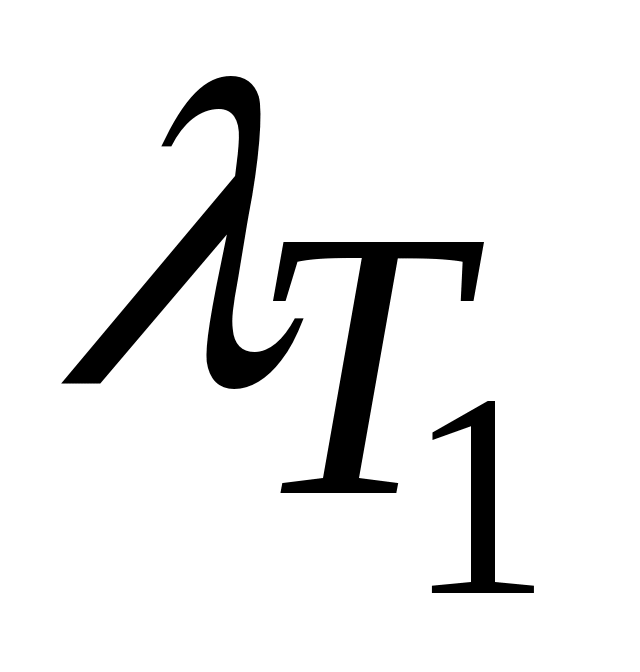 и
и 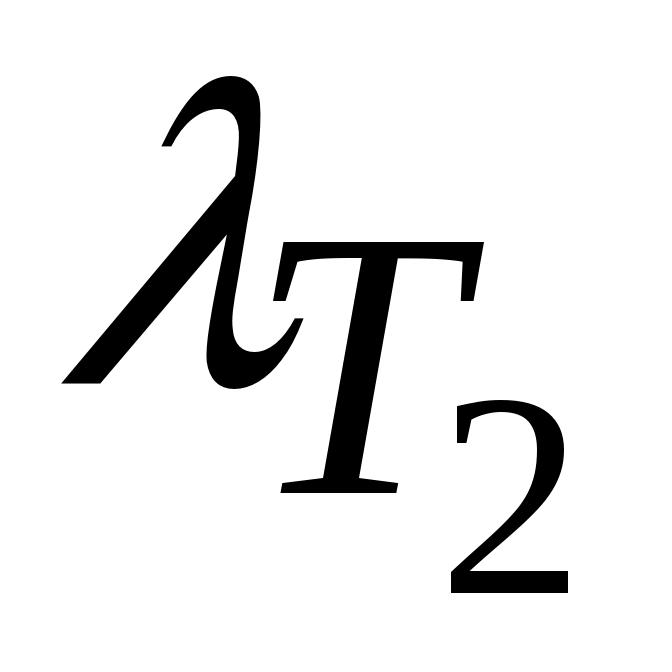 находим из таблицы А.1. с помощью интерполяции Лагранжа (см. Приложение, (А.1) )
находим из таблицы А.1. с помощью интерполяции Лагранжа (см. Приложение, (А.1) )
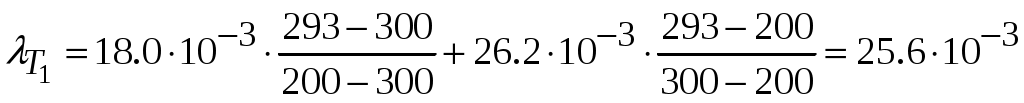 , Вт/(м·К)
, Вт/(м·К)
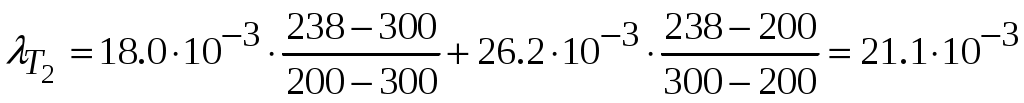 , Вт/(м·К)
, Вт/(м·К)
При линейной зависимости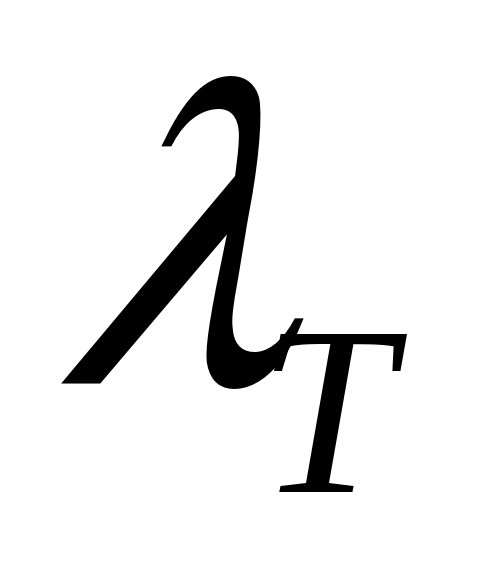 среднее значение коэффициента равно полусумме значений на границах интервала
среднее значение коэффициента равно полусумме значений на границах интервала 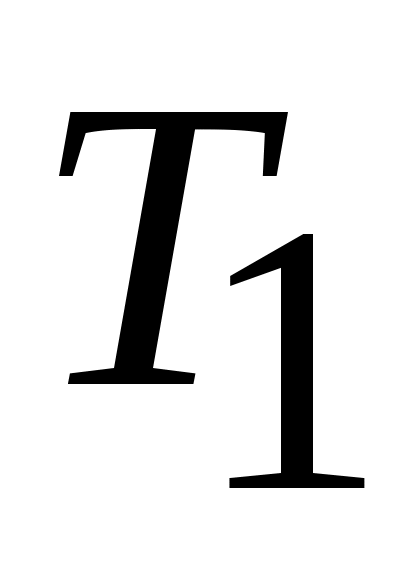 и
и 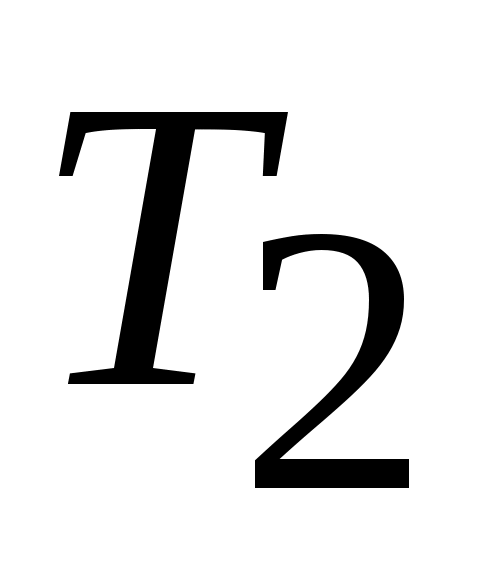
где
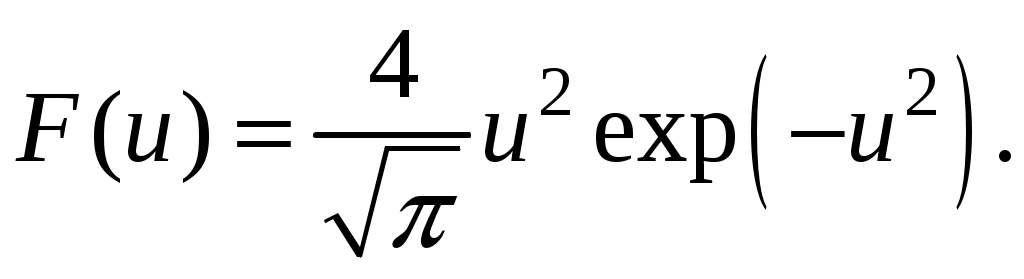 (7.2)
(7.2)Решение
Кинетическая энергия молекулы состоит из поступательной и вращательной энергий, суммарное значение которых равно 1 эВ. Атом гелия имеет 3 степени свободы. По закону равнораспределения на одну степень свободы молекулы приходится средняя энергия
Поэтому для атомов гелия мы имеем
тогда температура, при которой энергия атомов гелия равна 1 эВ будет определяться из следующей цепочки
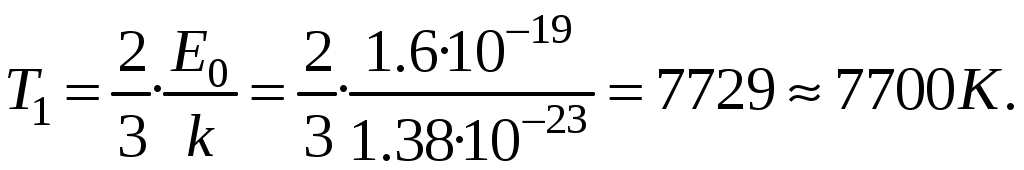
Относительная доля молекул идеального газа, чьи скорости лежат в диапазоне от
Для того, чтобы найти долю частиц, у которых скорости находятся в диапазоне от
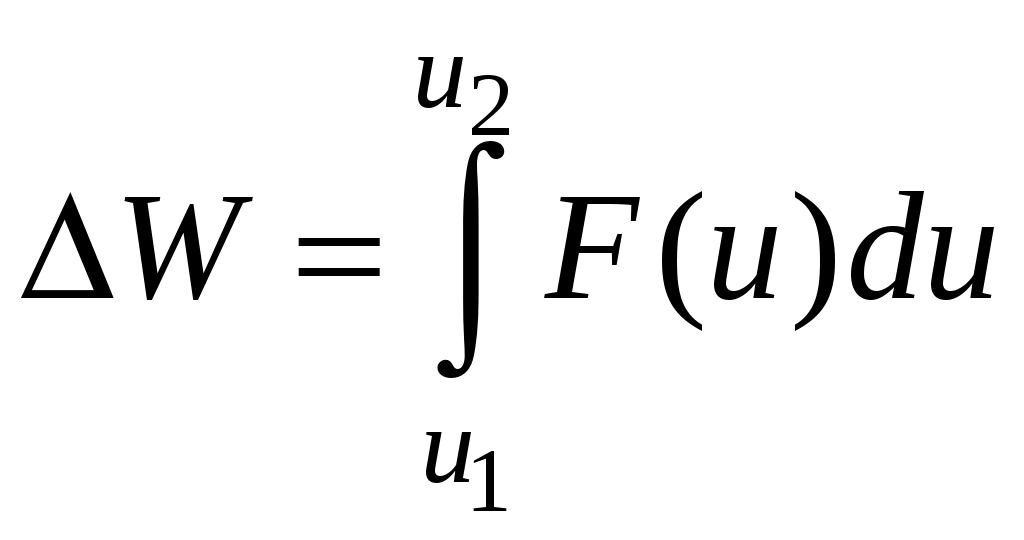 (7.5)
(7.5)Вычислим скорости
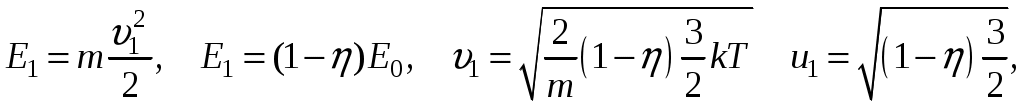 (7.6)
(7.6)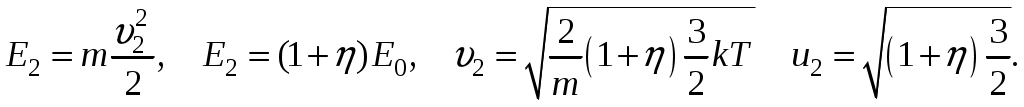 (7.7)
(7.7)Итак, скорости равны
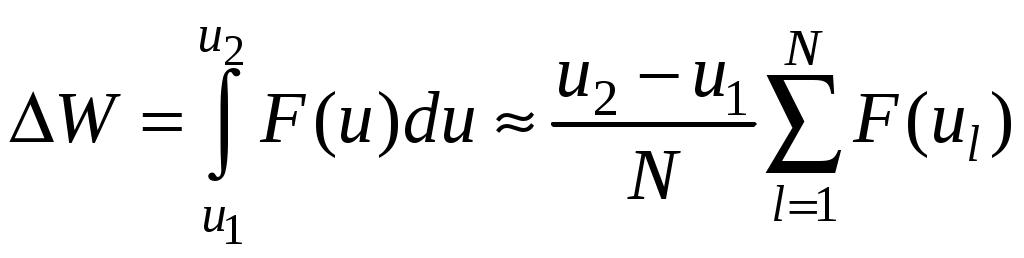 (7.8)
(7.8)реализованную в виде псевдокода
begin\\
q=1.6e-19;\\
k=1.38e-23;\\
E0=1*q;\\
i=3;\\
T1=2*E0/3/k\\
nu=0.25\\
u1=sqrt(1.3*(1-nu))\\
u2=sqrt(1.3*(1+nu))\\
N=500\\
du=(u2-u1)/N;\\
sums=0\\
for j=1:N\\
u=u1+j*du;\\
sums=sums+u*u*exp(-u*u);\\
end\\
DW=4*du*sums/sqrt(pi)\\
% Распределение молекул газа по скоростям
v1=0\\
v2=4\\
N=100\\
dv=(v2-v1)/N;\\
sums=0\\
for j=1:N\\
u=v1+j*dv;\\
v(j)=u;\\
f(j)=4*u*u*exp(-u*u)/sqrt(pi);\\
sums=sums+f(j);\\
end\\
DW0=dv*sums\\
end\\
Выполняя расчет (8.8), получаем
Построим график

Рис.7.1.Распределение молекул газа по скоростям
Анализ решения
Оценивая «на глаз» заштрихованную площадь и полученное численное значение вероятности
Ответ:
***
7.1. Энергию атомных и субатомных частиц часто измеряют в электрон-вольтах, 1 эВ = 1.6×10-19 Дж. Найти, при какой температуре средняя кинетическая энергия молекулы азота равна 1 эВ. Определить, при какой температуре 25% всех молекул имеют кинетическую энергию, превышающую 1 эВ. Постройте график зависимости
7.2. Азот массой 12 г находится в закрытом сосуде при температуре 300 К. Какое количество теплоты необходимо передать азоту, чтобы средняя квадратичная скорость молекул возросла в 2 раза? Привести поясняющий рисунок и указать основные параметры.
7.3. Газ, состоящий из жестких двухатомных молекул, находится при температуре 300 К. Вычислить среднюю квадратичную угловую скорость вращения молекулы, если ее момент инерции равен 2.1 10-46 кг м2. Привести поясняющий рисунок и указать основные параметры.
7.4. В вакуумном диоде электроны, эмитируемые накаленным катодом, попадают в задерживающее поле анода. До анода доходят лишь достаточно быстрые электроны. Считая, что тепловые скорости эмитируемых (вышедших из катода) электронов распределены по закону Максвелла с температурой 1150 К, определить долю электронов, преодолевающих задерживающий потенциал а) 0.2 В, б) 0.4 В. Катодом является тонкая прямолинейная нить, натянутая по оси цилиндрического анода. Привести поясняющий рисунок и указать основные параметры.
7.5. Найти отношение числа молекул водорода, скорости которых лежат в пределах от 3000 м/с до 3050 м/с, к числу молекул, имеющих скорости в пределах от 1550 м/с до 1600 м/с, если температура водорода 573 К. Постройте график зависимости
7.6. Какая часть молекул кислорода обладает скоростями, отличающимися от наивероятнейшей не больше чем на 25 м/с при температурах 273 К и 573 К? Постройте график зависимости
7.7. Определить отношение числа молекул водорода, обладающих скоростями в интервале от 2500 м/с до 2600 м/с, к числу молекул, обладающих скоростями от 1500 м/с до 1600 м/с, если температура водорода 273 К. Постройте график зависимости
7.8. Найти полное число молекул и их вес в столбе атмосферы с основанием 1 см
2 , если концентрация молекул у земли n0 = 2.691019 см-3 при Т = 273 К, = 0.029 кг/моль. Привести поясняющий рисунок и указать основные параметры.
7.9. Оценить порядок величины полного числа молекул в атмосфере Земли, считая, что плотность молекул описывается барометрической формулой при постоянной температуре Т=273 К, а радиус Земли равен 6370 км. Привести поясняющий рисунок и указать основные параметры.
7
 .10. (См.[3]) Дымовая труба высотой 150 м выпускает дым при температуре
.10. (См.[3]) Дымовая труба высотой 150 м выпускает дым при температуре 7.11. Для определения числа Авогадро Перрен измерял распределение по высоте шарообразных частиц гуммигута, взвешенных в воде. Он нашел , что отношение количества частиц в слоях, отстоящих друг от друга на расстоянии 30 мкм, равно 2.08. Плотность частиц 1194 кг/м3, воды 1000 кг/м3. Радиусы частиц 0.212 мкм. На основании этих данных вычислите число Авогадро. Температура воды 18о С. Привести поясняющий рисунок и указать основные параметры.
7.12. Вычислить наиболее вероятную энергию молекул в идеальном газе и показать, что эта энергия не равна
8. Явления переноса
Пример 8.1 Теплопроводность. Сколько теплоты протекает через окно с двойной рамой за один час, если окно имеет размеры 0.76х1.12 м? Толщина слоя воздуха между рамами 0.16 м, температура наружнего воздуха –350 С, а внутри дома 200 С.

Теплопотери через окно можно вычислить на основе эмпирического закона Фурье (см., например, [7] с.86)
Здесь Q - количество теплоты, переданное через окно, площадью
где
Теплопроводность воздуха является одной из важнейших характеристик, используемых при проектировании различных сооружений, в двигателестроении, в химической технологии и т.п., поэтому имеются обширные таблицы этой величины, измеренной при различных давлениях и температурах. Воспользуемся опытными данными, взятыми из справочника [8] (с. 345) и приведенными в Приложении. Как видно из рис.А.1 зависимость
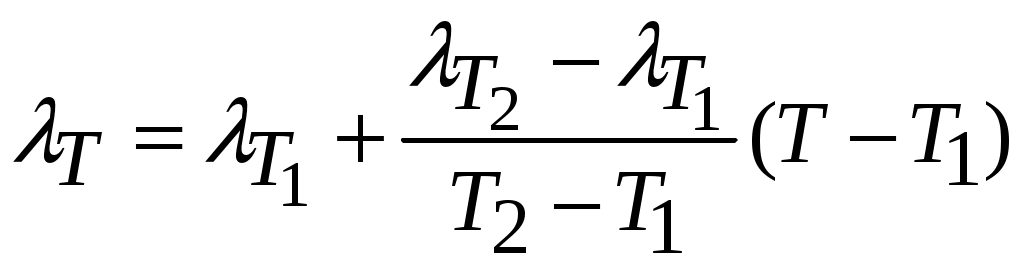 (8.3)
(8.3)где значения
При линейной зависимости