ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 1093
Скачиваний: 24
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
13.7.Найти объемную плотность энергии электрического поля в точке, находящейся: а) на расстоянии 2 см от поверхности заряженного шара радиусом 1 см; б) вблизи бесконечной заряженной плоскости; в) на расстоянии 2 см от бесконечно длинной заряженной нити. Поверхностная плотность заряда шара и плоскости 16.7 мкКл/м2, линейная плотность заряда нити 167 нКл/м. Диэлектрическая проницаемость среды
13.8. Две концентрические сферические поверхности, находящиеся в вакууме, имеют равномерно распределенные одинаковые заряды 5 мкКл. Радиусы этих поверхностей 1 и 2 м. Найти энергию электрического поля, заключенную между этими сферами. Привести поясняющий рисунок и указать основные параметры
13.9. Две концентрические сферические поверхности, находящиеся в вакууме, имеют равномерно распределенные одинаковые заряды 5 мкКл. Радиусы этих поверхностей 1 и 2 см. Найти энергию электрического поля, заключенную между этими сферами. Привести поясняющий рисунок и указать основные параметры
13.10. Две концентрические сферические поверхности, находящиеся в вакууме, имеют равномерно распределенные одинаковые заряды 5 мкКл. Радиусы этих поверхностей 1 и 2 мм. Найти энергию электрического поля, заключенную между этими сферами. Привести поясняющий рисунок и указать основные параметры
14. Постоянный ток. Закон Ома. Закон Джоуля-Ленца
Пример 14.1. (Квант, 2012, №3, стр.19, Ф2272). В электрической схеме, изображенной на рис.14.1, все батарейки одинаковые, идеальные и имеют ЭДС
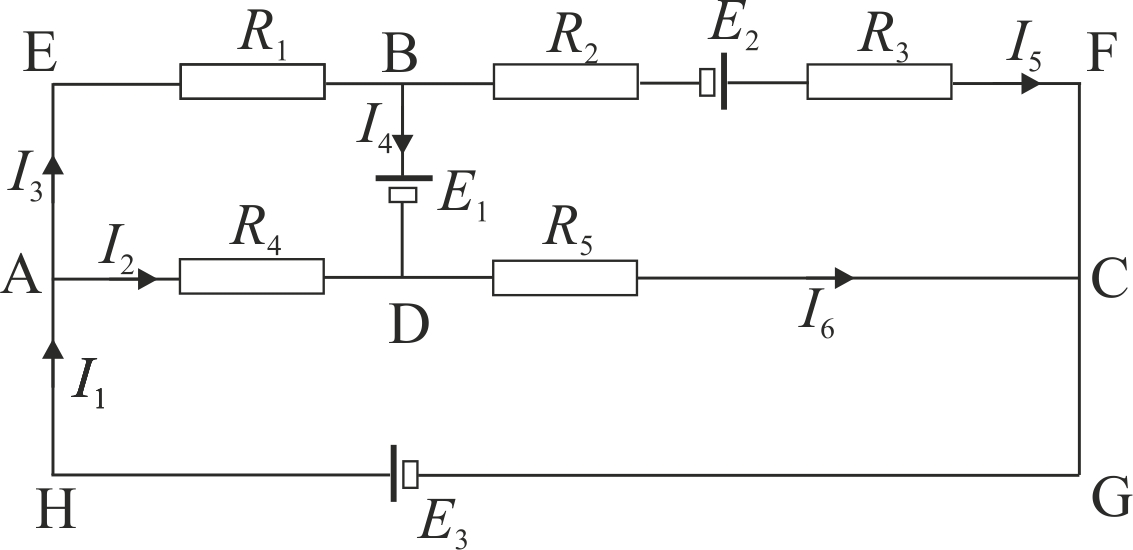
Рис.14.1. Электрическая схема цепи
Математическая модель
В каждом узле алгебраическая сумма сил токов равна нулю. Токи, идущие к узлу положительны, а токи, исходящие из узла, — отрицательные.
В произвольном замкнутом контуре сложной разветвленной цепи алгебраическая сумма электродвижущих сил равна сумме произведений сил токов в отдельных участках контура на их сопротивления. При этом надо задать произвольно направление обхода контура и направления токов в контуре. Все участки контура обойти в одном направлении. Если это направление совпадает с направлением тока, то слагаемое
Решение
Согласно схеме (рис.14.1), необходимо найти шесть неизвестных величин – токов, поэтому надо составить систему уравнений из шести линейно-независимых уравнений.
В схеме имеется 4 узла - A, B, C, D, тогда независимых уравнений можно составить на единицу меньше, чем узлов схемы [2].
Применяем первое правило Кирхгофа к любым трем узлам
Узел A:
Узел B:
Узел D:
Оставшиеся три уравнения составим по второму правилу Кирхгофа для трех замкнутых контуров цепи, например, AEBD, BFCD, ACGH.
Будем считать, что направление обхода в каждом контуре цепи проводится по часовой стрелке.
Контур AEBD
Контур BFCD
Контур ACGH
Представим систему (3)-(8) в виде матричного уравнения
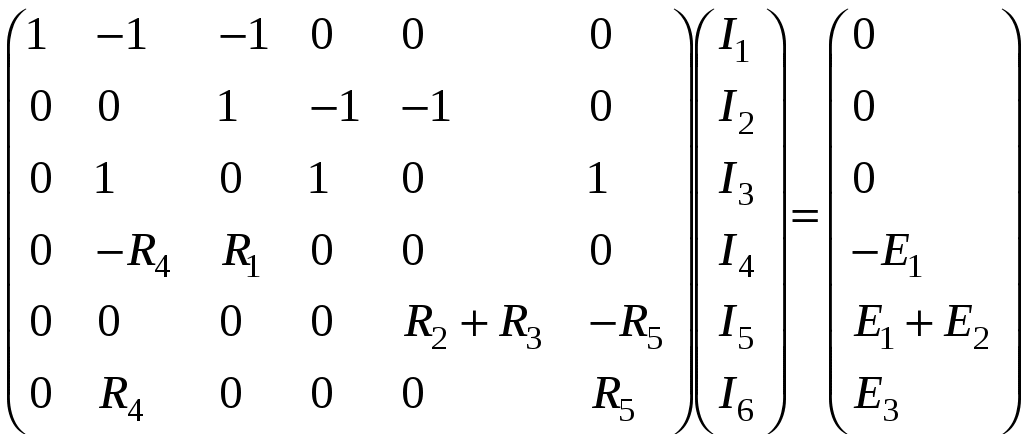 (9)
(9)или в сокращенном виде
Решение матричного уравнения
(10)
можно найти разными методами, но достаточно найти решение численно, например при помощи метода Гаусса (см. Приложение А1) или на основе математического пакета. Здесь приведен листинг программы решения системы (9) на языке программирования пакета MatLab [5].
%F2272.m
clear all
E1=1; E2=1; E3=1;
R1=10; R2=10; R3=10; R4=10; R5=10;
M=zeros(6,6);
M(1,1)= 1; M(1,2)=-1; M(1,3)=-1;
M(2,3)= 1; M(2,4)=-1; M(2,5)=-1;
M(3,2)= 1; M(3,4)= 1; M(3,6)= 1;
M(4,2)=-R4; M(4,3)= R1;
M(5,5)= R2+R3; M(5,6)=-R5;
M(6,2)= R4; M(6,6)= R5;
B=zeros(6,1);
B(4)=-E1;
B(5)= E1+E2;
B(6)= E3;
I=M\B
%Проверка решения
Y=M*I-B
Как показывает результаты вычислений, вычислительная ошибка
Ответ:
***
14.1. Какую массу топлива нужно сжечь на электростанции, чтобы по телевизору мощностью 250 Вт посмотреть фильм продолжительностью 1.5 часа? Построить диаграмму «масса топлива - тип электростанции», если известно, что: кпд электростанции 30%, удельная теплота сгорания нефти 46 МДж/кг, кпд электростанции 24%, удельная теплота сгорания угля 28,8 МДж/кг, кпд АЭС 35%, удельная теплота сгорания уранового топлива 8,28ּ1013 Дж/кг.
14.2. Электрический чайник вместимости 1.5 литров имеет сопротивление нагревательного элемента 50 Ом, кпд 70 % и работает при напряжении 220 В. Начальная температура воды 10 градусов. Определить мощность тока, потребляемую чайником; силу тока в нагревательном элементе; время, в течение которого вода в чайнике закипит, и стоимость энергии, если 1 кВтּчас стоит 2 рубля 9 копеек (на осень 2013 года, отметим, что весной 2003 года 1 кВтּчас стоил 88 копеек). А какова стоимость энергии сейчас? Привести поясняющий рисунок и указать основные параметры
14.3. Имеется 12 элементов с ЭДС 1.5 В и внутренним сопротив-лением 0.4 Ом каждый. Как нужно соединить эти элементы
, чтобы получить наибольшую силу тока во внешней цепи, имеющей сопротивление 0.3 Ом? Какой величины будет ток? Постройте графики полной, полезной мощности и мощности потерь.
14.4. Определите силу тока, протекающего через сопротивление R1 в цепи, изображенной на рисунке 15.2. Параметры цепи следующие: R1 = 2 кОм, R2 = 1 кОм, R3 = 2 кОм, r = 0 Ом и U = 24 В. Построить график падения потенциала вдоль замкнутого контура ABCFA. Указание: см. пример 2.12 в [4].
14.5. Определите силу тока, протекающего через сопротивление R1 в цепи, изображенной на рисунке 14.2. Параметры цепи следующие: R1 = 2 кОм, R2 = 1 кОм, R3 = 2 кОм, r = 0 Ом и U = 24 В. Построить график падения потенциала вдоль замкнутого контура ABCDEFA. Указание: см. пример 2.12 в [4].
15.6. Два гальванических элемента, имеющих ЭДС E1 = 1.5 В, E2 = 1.6 В и внутренние сопротивления r1 = 0.60 Ом, r2 = 0.40 Ом, соединены разноименными полюсами (рис.15.3). Пренебрегая сопротивлением соединительных проводов, определите разность потенциалов на зажимах элементов. Построить график падения потенциала вдоль цепи. Указание: см. пример 2.12 в [4].
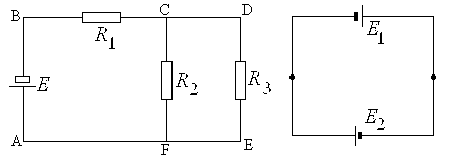
Рис. 14.2. К задаче 14.4, 14.5. Рис. 14.3. К задаче 14.6.
14.7. Три источника с ЭДС E1 = 10.0 В, E2 = 5.0 В, E3 = 6.0 В и внутренними сопротивлениями r1 = 0.1 Ом, r2 = 0.2 Ом, r3 = 0.1 Ом соединены, как показано на рисунке 14.4. Определить напряжение на резисторах сопротивлениями R1 = 5.0 Ом, R2 = 1.0 Ом, R3= 3.0 Ом. Построить график падения потенциала вдоль замкнутого контура ABCDEHGKA. Указание: см. пример 2.12 в [4].
14.8. Три источника с ЭДС E1 = 9.0 В, E2 = 6.0 В, E3 = 5.0 В и внутренними сопротивлениями r1 = 0.1 Ом, r2 = 0.2 Ом, r3 = 0.3 Ом соединены, как показано на рисунке 14.4. Определить напряжение на резисторах сопротивлениями R1 = 5.0 Ом, R2 = 2.0 Ом, R3= 3.0 Ом. Построить график падения потенциала вдоль замкнутого контура ABFHGKA. Указание: см. пример 2.12 в [4].
14.9. Цепь собрана из одинаковых резисторов и одинаковых вольтметров (рис.14.5). Показания первого вольтметра
U1 =1.25 В и третьего вольтметра U3=0.4 В. Найти показание второго вольтметра U2. Построить график падения потенциала вдоль замкнутого контура ABCGA. Указание: см. пример 2.12 в [4].
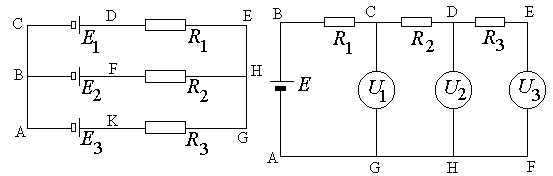
Рис.14.4. К задаче 14.7, 14.8 Рис.14.5. К задаче 14.9
14.10. Определить сопротивление подводящих проводов от источника с напряжением 220 В, если при коротком замыкании предохранители из свинцовой проволоки площадью сечения 1 мм2 и длиной 2 см плавятся за 0,03 секунды. Начальная температура 270 С. Удельная теплоемкость свинца равна 26.44 Дж/(кг К), удельная теплота плавления 4,77 кДж/кг, температура плавления t*=3270 С, плотность свинца 11340 кг/м3. Привести поясняющий рисунок и указать основные параметры
-
Магнитное поле в вакууме
15.1. По длинному проводу, согнутому под прямым углом, течет ток, равный 12 А. Какой будет напряженность магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины на расстоянии 0.025 м? Построить картину силовых линий и график напряженности магнитного поля, вдоль биссектрисы.
15.2. Рядом с длинным проводом, по которому течет ток 2.5 А, расположена квадратная рамка с током 4 А. Рамка и провод лежат в одной плоскости. Проходящая через середины противолежащих сторон ось рамки параллельна проводу и отстоит от него на расстоянии 40 мм. Сторона рамки 20 мм. Найти силу, действующую на рамку. Построить картину силовых линий.
15.3. Рядом с длинным проводом, по которому течет ток 3.0 А, расположена квадратная рамка с током 5 А. Рамка и провод лежат в одной плоскости. Проходящая через середины противолежащих сторон ось рамки параллельна проводу и отстоит от него на расстоянии 50 мм. Сторона рамки 20 мм. Найти работу, которую нужно совершить против сил магнитного поля, чтобы повернуть рамку на 180 градусов. Построить картину силовых линий.
15.4. Батарея аккумуляторов с ЭДС 24 В и внутренним сопротивлением 0.01 Ом соединена с потребителем двумя медными проводами, расположенными на расстоянии 5 см один от другого. Провода закреплены на изоляторах, расстояние между которыми 0.5 м. Определить силу, действующую на изоляторы при коротком замыкании на зажимах потребителя, если длина подводящей линии 20 м, а сечение проводов 3 мм2. Построить картину силовых линий индукции магнитного поля.