ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 53
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
«АЛГЕБРА» пәнінен IV-тоқсанның №1 «Теңсіздіктер» ббжб тапсырмалары.
Мерзімі: 05.05.2022 Сыныбы: 8
| № | Тапсырмалар | Дескрипторы | Балл | |
| 1 | х-тің қандай мәнінде 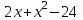 өрнегі теріс мәндер қабылдайды? өрнегі теріс мәндер қабылдайды? | -квадрат үшмүшенің түбірлерін табады; - квадрат үшмүше мәндерінің оң (теріс) болатын аралықтарын табады; - жауабын жазады; | 3 | |
| 2 | Тіктөртбұрыштың ұзындығы енінен 4 см-ге артық. Егер тіктөртбұрыштың ауданы 96 см2 -тан артық болса, оның өлшемдері қандай болуы мүмкін? | - квадрат теңсіздікті құрады; - теңсіздікті шешу тәсілін таңдайды; - теңсіздікті шешеді; -есептің жауабын жазады; | 4 | |
| 3 | Теңсіздікті шешіңіз: 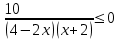 | - теңсіздікті шешу әдісін анықтайды; - ММЖ табады; - аралықтарда таңбаларды анықтайды; - жауабын жазады; | 4 | |
| 4 | Теңсіздіктер жүйесін шешіңіз: 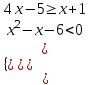 | - сызықтық теңсіздіктің шешімдер жиынын табады; - квадрат үшмүшенің түбірлерін табады; - квадрат үшмүше мәндерінің оң (теріс) болатын аралықтарын табады; - квадрат теңсіздіктің шешімін табады; - теңсіздіктердің шешімдерінің қиылысуын табады; | 5 | |
| Жалпы: | 16 | |||
«АЛГЕБРА» пәнінен IV-тоқсанның №1 «Теңсіздіктер» ббжб тапсырмалары.
Мерзімі: 05.05.2022 Сыныбы: 8
| № | Тапсырмалар | Дескрипторы | Балл | |
| 1 | х-тің қандай мәнінде 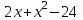 өрнегі теріс мәндер қабылдайды? өрнегі теріс мәндер қабылдайды? | -квадрат үшмүшенің түбірлерін табады; - квадрат үшмүше мәндерінің оң (теріс) болатын аралықтарын табады; - жауабын жазады; | 3 | |
| 2 | Тіктөртбұрыштың ұзындығы енінен 4 см-ге артық. Егер тіктөртбұрыштың ауданы 96 см2 -тан артық болса, оның өлшемдері қандай болуы мүмкін? | - квадрат теңсіздікті құрады; - теңсіздікті шешу тәсілін таңдайды; - теңсіздікті шешеді; -есептің жауабын жазады; | 4 | |
| 3 | Теңсіздікті шешіңіз: 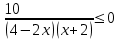 | - теңсіздікті шешу әдісін анықтайды; - ММЖ табады; - аралықтарда таңбаларды анықтайды; - жауабын жазады; | 4 | |
| 4 | Теңсіздіктер жүйесін шешіңіз: 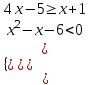 | - сызықтық теңсіздіктің шешімдер жиынын табады; - квадрат үшмүшенің түбірлерін табады; - квадрат үшмүше мәндерінің оң (теріс) болатын аралықтарын табады; - квадрат теңсіздіктің шешімін табады; - теңсіздіктердің шешімдерінің қиылысуын табады; | 5 | |
| Жалпы: | 16 | |||
«ГЕОМЕТРИЯ» пәнінен IV-тоқсанның №1 «Жазықтықтағы тікбұрышты координаталар жүйесі» ббжб тапсырмалары.
Мерзімі: 03.05.2022 Сыныбы: 8
| № | Тапсырмалар | Дескрипторы | Балл | ||
| 1 | С нүктесі АВ кесіндісінің ортасы. Егер С(-4;5) және А(-6;-7) болса В нүктесінің координатасын табыңыз. | -кесіндінің ортасының координатасы мен бір ұшының координатасы арқылы екінші ұшының координатасын өрнектейді; -нүктенің координатасын табады; | 2 | ||
| 2 | а) АВ центрі О болатын шеңбер диаметрі. Егер А(3;7) және B(5;-1) болса, шеңбер центрінің координатасын табыңыз; б) пункті бойынша шеңбер теңдеуін жазыңыз; | а | -кесінді ұштарының координаталары арқылы кесінді ортасының координатасын өрнектейді; -шеңбер центрінің координатасын табады; | 4 | |
| б | -шеңбер радиусын анықтайды; -шеңбер теңдеуін жазады; | ||||
| 3 | 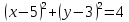 және және 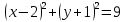 теңдеулерімен берілген екі шеңберді салып, олардың өзара орналасулары н анықтаңдар. теңдеулерімен берілген екі шеңберді салып, олардың өзара орналасулары н анықтаңдар. | -бірінші шеңберді салады; -екінші шеңберді салады; -екі шеңбердің өзара орналасуына қорытынды жасайды; | 3 | ||
| 4 | А(-6;3), B(2;3), C(4;3), D(-6;-3) нүктелері табаны АВ мен СД болатын тікбұрышты трапецияның төбелері. Трапецияның орта сызығы мен ауданын табыңыз | -бүйір қабырғаларының орталарының координаталарын немесе трапеция табандарының ұзындығын табады; -орта сызығын табады; - бүйір қабырғаларының ұзындығын табады; -бүйір қабырғаларының қайсысы биіктік екенін анықтайды; -трапеция ауданын табады; | 5 | ||
| Жалпы: | 14 | ||||
«ГЕОМЕТРИЯ» пәнінен IV-тоқсанның №1 «Жазықтықтағы тікбұрышты координаталар жүйесі» ббжб тапсырмалары.
Мерзімі: 03.05.2022 Сыныбы: 8
| № | Тапсырмалар | Дескрипторы | Балл | ||
| 1 | С нүктесі АВ кесіндісінің ортасы. Егер С(-4;5) және А(-6;-7) болса В нүктесінің координатасын табыңыз. | -кесіндінің ортасының координатасы мен бір ұшының координатасы арқылы екінші ұшының координатасын өрнектейді; -нүктенің координатасын табады; | 2 | ||
| 2 | а) АВ центрі О болатын шеңбер диаметрі. Егер А(3;7) және B(5;-1) болса, шеңбер центрінің координатасын табыңыз; б) пункті бойынша шеңбер теңдеуін жазыңыз; | а | -кесінді ұштарының координаталары арқылы кесінді ортасының координатасын өрнектейді; -шеңбер центрінің координатасын табады; | 4 | |
| б | -шеңбер радиусын анықтайды; -шеңбер теңдеуін жазады; | ||||
| 3 |  және және  теңдеулерімен берілген екі шеңберді салып, олардың өзара орналасулары н анықтаңдар. теңдеулерімен берілген екі шеңберді салып, олардың өзара орналасулары н анықтаңдар. | -бірінші шеңберді салады; -екінші шеңберді салады; -екі шеңбердің өзара орналасуына қорытынды жасайды; | 3 | ||
| 4 | А(-6;3), B(2;3), C(4;3), D(-6;-3) нүктелері табаны АВ мен СД болатын тікбұрышты трапецияның төбелері. Трапецияның орта сызығы мен ауданын табыңыз | -бүйір қабырғаларының орталарының координаталарын немесе трапеция табандарының ұзындығын табады; -орта сызығын табады; - бүйір қабырғаларының ұзындығын табады; -бүйір қабырғаларының қайсысы биіктік екенін анықтайды; -трапеция ауданын табады; | 5 | ||
| Жалпы: | 14 | ||||
«АЛГЕБРА» пәнінен IV-тоқсанның №1 «Тригонометрия» ббжб тапсырмалары.
Мерзімі: 14.04.2022 Сыныбы: 9
| № | Тапсырмалар | Дескрипторы | Балл |
| 1 | Есептеңіз: sin1050 - sin750 | -синустардың көбейтіндісін қосындыға түрлендіру формуласын қолданады; -өрнекті ықшамдайды; | 2 |
| 2 | Ықшамдаңыз: 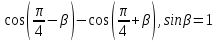 | -косинустардың көбейтіндісін қосындыға түрлендіру формуласын қолданады; -өрнекті ықшамдайды; -синустың мәнін табады; -өрнекті ықшамдайды; | 4 |
| 3 | Дәлелдеңдер: 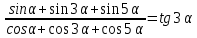 | -топтастыруды орындайды; -косинустардың көбейтіндісін қосындыға түрлендіру формуласын қолданады; -синустардың көбейтіндісін қосындыға түрлендіру формуласын қолданады; -негізгі тригонометриялық ұқсастықты қолданады; -теңдік туралы қорытынды жасайды; | 5 |
| Жалпы: | 11 | ||
«АЛГЕБРА» пәнінен IV-тоқсанның №1 «Тригонометрия» ббжб тапсырмалары.
Мерзімі: 14.04.2022 Сыныбы: 9
| № | Тапсырмалар | Дескрипторы | Балл |
| 1 | Есептеңіз: sin1050 - sin750 | -синустардың көбейтіндісін қосындыға түрлендіру формуласын қолданады; -өрнекті ықшамдайды; | 2 |
| 2 | Ықшамдаңыз:  | -косинустардың көбейтіндісін қосындыға түрлендіру формуласын қолданады; -өрнекті ықшамдайды; -синустың мәнін табады; -өрнекті ықшамдайды; | 4 |
| 3 | Дәлелдеңдер:  | -топтастыруды орындайды; -косинустардың көбейтіндісін қосындыға түрлендіру формуласын қолданады; -синустардың көбейтіндісін қосындыға түрлендіру формуласын қолданады; -негізгі тригонометриялық ұқсастықты қолданады; -теңдік туралы қорытынды жасайды; | 5 |
| Жалпы: | 11 | ||
«АЛГЕБРА» пәнінен IV-тоқсанның №1 «Тригонометрия» ббжб тапсырмалары.
Мерзімі: 14.04.2022 Сыныбы: 9
| № | Тапсырмалар | Дескрипторы | Балл |
| 1 | Есептеңіз: sin1050 - sin750 | -синустардың көбейтіндісін қосындыға түрлендіру формуласын қолданады; -өрнекті ықшамдайды; | 2 |
| 2 | Ықшамдаңыз:  | -косинустардың көбейтіндісін қосындыға түрлендіру формуласын қолданады; -өрнекті ықшамдайды; -синустың мәнін табады; -өрнекті ықшамдайды; | 4 |
| 3 | Дәлелдеңдер:  | -топтастыруды орындайды; -косинустардың көбейтіндісін қосындыға түрлендіру формуласын қолданады; -синустардың көбейтіндісін қосындыға түрлендіру формуласын қолданады; -негізгі тригонометриялық ұқсастықты қолданады; -теңдік туралы қорытынды жасайды; | 5 |
| Жалпы: | 11 | ||
«АЛГЕБРА» пәнінен IV-тоқсанның №2 «Ықтималдықтар теориясының элементтері» ббжб тапсырмалары.
Мерзімі: 05.05.2022 Сыныбы: 9
| № | Тапсырмалар | Дескрипторы | Балл |
| 1 | 1.5×4 см2 тіктөртбұрышқа іштей сызылған шеңбердің радиусы 1,5 см., радиус шеңбері жазылған. Тіктөртбұрышқа кездейсоқ қойылған нүкте шеңбердің ішінде болмауы ықтималдығы қандай? Жауапты мыңға дейін жуықтаңыз. | -шаршының ауданын табу үшін өрнек құрастырады; -шеңбер ауданы үшін өрнек құрайды; -геометрияның ықтималдығынын анықтамасын пайдаланады; -шеңберге түсу ықтималдығын табады; -қарама-қарсы оқиғалардың ықтималдығын табу және жауапты дөңгелектейді; | 5 |
| 2 | Жәшікте 90 шар,олар 1,2,…,90-ге дейін белгіленген. Жәшіктен кездейсоқ бір шар алынды. Алынған шардың 6 сан болатын ықтималдығын табыңыз? | -саны бар шарлар санын табады 5, бесінші ондықта; -саны бар шарлар санын табады 5, қалған ондықтарда; -ықтималдықты формула бойынша табады; | 3 |
| 3 | Бір уақытта екі ойын сүйегі лақтырылды. Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 8 болу ықтималдылығын табыңыз? | -осы оқиғалар үшін барлық мүмкін болатын нәтижелер санын табады; -осы оқиғаға қолайлы нәтиже санын табады; -ықтималдықты формула бойынша табады; | 3 |
| 4 | Фабрикада сөмкелер шығарылады. 100 сөмкенің ішінде 8-інде ақауы кездеседі. Кездейсоқ алынған сөмкенің ақауысыз болуының ықтималдығын табыңыз. | -ықтималдықтың классикалық формуласын пайдаланады; -барлық мүмкін болатын нәтижелер санын табады; -ықтималдықтың мәнін табады; -барлық мүмкін болатын нәтижелер санын табады; | 4 |
| 5 | Такси фирмасында кәзіргі уақытта 20 көлік бар: 10 қара, 2 сары және 8 жасыл. Шақыру тапсырыс берген адамға ең жақын көлік шықты. Кездейсоқ шыққан көліктің жасыл болуының ықтималдығын табыңыз. | -шарты бойынша қолайлы саны нәтижелерін анықтайды; -кездейсоқты формула бойынша табады; | 2 |
| Жалпы: | 17 | ||