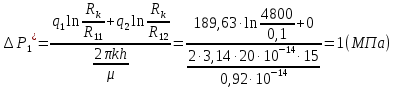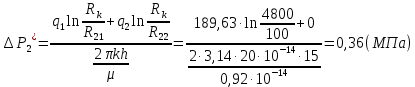Файл: Курс Модели оптимальной разработки и обустройства месторождений нефти и газа Домашнее задание 1 Оптимизация режимов эксплуатации скважин.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 28
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
РГУ нефти и газа (НИУ) имени И.М. Губкина
Факультет разработки нефтяных и газовых месторождений
Кафедра управление разработкой нефтяных месторождений
Курс: «Модели оптимальной разработки и обустройства месторождений нефти и газа»
Домашнее задание №1 «Оптимизация режимов эксплуатации скважин»
Вариант №1
Выполнил:
студент группы РНМ-22-04
Баринов Н.В.
Проверил:
профессор, д.т.н.
Ермолаев А. И.
Москва 2023
ЗАДАНИЕ
Рассматривается эксплуатация 2-х нефтяных добывающих скважин при естественном режиме работы пласта, i=1,2.
Исходные параметры (Вариант 1):
с1=0,15 – доля нефти в продукции 1-й скважины;
с2=0,93 – доля нефти в продукции 2-й скважины;
ΔPmax1=1,5 МПа – максимально допустимый перепад между давлением на контуре питания залежи и забойным давлением 1-й скважины;
ΔPmax2=1,5 МПа – максимально допустимый перепад между давлением на контуре питания залежи и забойным давлением 2-й скважины;
Rк=4,8 км – радиус контура питания залежи;
R12=R21=100 м - расстояние между скважинами;
R11=R22=Rc=0,1 м – радиус скважин;
h =15 м – толщина пласта;
k=0,2 Д – проницаемость пласта;
μ=0,8 сПз – вязкость пластового флюида.
Свободные переменные: q2, q3.
Требуется найти: такие дебиты скважин по жидкости – q1 и q2 и забойные давления скважин – Р1 и Р2, которые обеспечат максимальный суммарный дебит по нефти при выполнении ограничения на величину перепадов между давлением на контуре питания залежи и забойными давлениями скважин.
Решение:
Процесс эксплуатации группы взаимовлияющих скважин описывается системой линейных уравнений относительно qi и Pi – параметров, характеризующих режимы работы скважин:
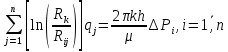
(1)
Математическая постановка задачи имеет вид модели линейного программирования:
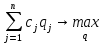 (2)
(2)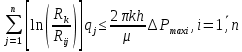 (3)
(3)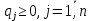 (4)
(4)Если найдены дебиты скважин, то при известном давлении на контуре питания по формулам (1) не трудно определить их забойные давления.
С учетом формул (2) - (4) математическая постановка задачи имеет вид:
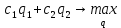 (5)
(5)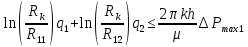 (6)
(6)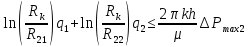 (7)
(7)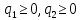 (8)
(8)Определим числовые значения параметров, входящих в задачу (5) - (8):
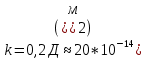 ;
;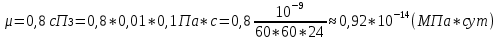 ;
;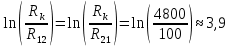
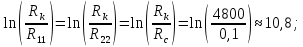
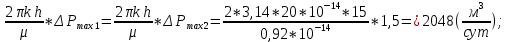
Теперь задача (5) - (8) принимает вид:
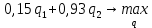 (9)
(9)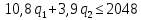 (10)
(10)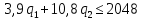 (11)
(11)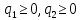 (12)
(12)Дополняя задачу (9) - (12) искусственными переменными q3 и q4, которые
также должны подчиняться условию (12), ограничения-неравенства (10) и (11)
можно заменить ограничениями-равенствами. После этого симплекс-методом
подлежит решению задача:
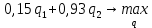 (13)
(13)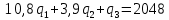 (14)
(14)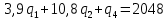 (15)
(15)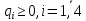 (16)
(16)Итерация № 1.
Шаг 1. Пусть свободными переменными являются q2 и q3, а базисными, соответственно, q1 и q4.
Шаг 2. Выразим базисные переменные через свободные, исходя из уравнений (14), (15):
-
из уравнения (14):
10,8q1 = 2048 – 3,9q2 – q3
q1 = 189,63 – 0,36q2 – 0,09q3; (17)
-
из уравнений (15) и (17):
q4 = 2048 – 3,9q1 – 10,8q2 = 2048 – 3,9(189,63 – 0,36q2 – 0,09q3) – 10,8q2 = 2048 – 739,56 + 1,4q2 + 0,35q3 – 10,8q2;
q4 = 1308,44 – 9,4q2 + 0,35q3 (18)
Проверим чему окажутся равны q1 и q4, если положить q2=q3=0: q1 =189,63≥0, q4=1308,44>0. Следовательно, можно переходить к шагу 3.
Шаг 3. Выразим функцию цели (13) только через свободные:
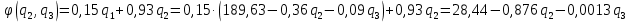 (19)
(19)Анализируя формулу (19), можно сделать вывод, что условие оптимальности выполнено: в функции цели (19) все коэффициенты при свободных переменных не имеют строго положительных значений. Поэтому оптимальное решение задачи (13)-(16) имеет вид: q3=0; q4=1308,44; q1=189,63; q2=0. При этом суммарный дебит по нефти составит 199,31 м3/сут.
Анализируя формулу (19), можно сделать вывод, что условие оптимальности выполнено: в функции цели (19) все коэффициенты при свободных переменных не имеют строго положительных значений. Поэтому оптимальное решение задачи (13)-(16) имеет вид: q3=0; q4=1308,44; q1=189,63; q2=0. При этом суммарный дебит по нефти составит 28,39 м3/сут.
Из полученных результатов и уравнений (1) следует, что ΔPi* – разность между давлением на контуре питания залежи и оптимальным забойным давлением i-й скважины (i=1,2):
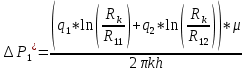 (20)
(20)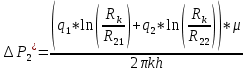 (21)
(21)Таким образом, согласно (20)-(21) разность между давлением на контуре питания залежи и оптимальным забойным давлением i-й скважины (i=1,2) равняется максимально допустимому перепаду: так как скважина 2 не работает, то ΔР2* будет меньше, чем максимально допустимый перепад, ΔР1*= =1 Мпа.