Файл: Решение Линейная функция спроса имеет вид 1) Где Qd объем спроса на благо.docx

Практическое задание 4

1. 
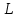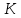   Технологическая норма замещения факторов и равна 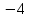. Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактор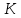а на 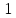единиц. Сколько дополнительных единиц фактора 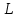потребуется фирме?
   

Решение

Условие оптимального использования ресурсов: .

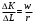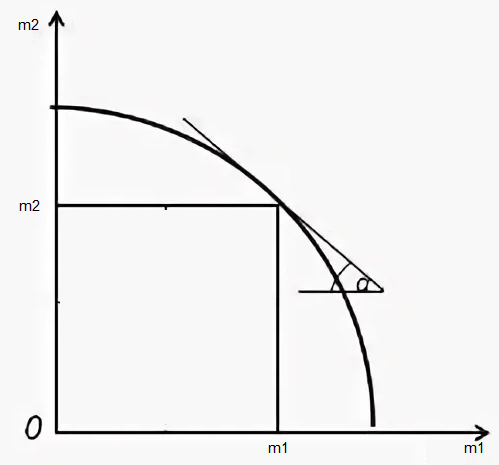
Графическое решение представлено на рисунке 4.



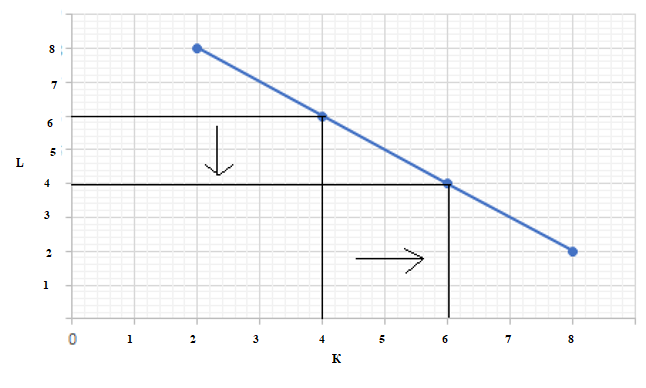
Вывод: в результате проведенных расчетов потребуется на 0,5 больше единиц труда.

Практическое задание 5

1. Предположим, что на рынке действуют две фирмы, функции общих издержек 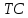заданы уравнениям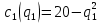и: и 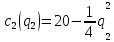. Рыночный спрос описывается функцией:

,

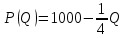где .

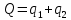Определите объем продаж, который будет у каждой фирмы, и цену, которая установится на рынке, если:

- фирмы конкурируют по Курно;

- фирмы конкурируют по Бертрану;

- фирмы конкурируют по сценарию Штакельберга.

Изобразите решение на графике.

Решение

1. 
   Стратегия по Курно предполагает объемную конкуренцию олигополистов: каждый из них выбирает объем продаж, максимизирующий его прибыль при условии, что его конкуренты не изменяют своих объемов продаж. Равновесие Курно — состояние рынка, при котором каждый участник понес бы потери, изменив свой выбор в одностороннем порядке.
   

Решение задачи по Курно:

Выведем уравнение реакции для фирмы I. Ее прибыль

---

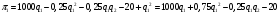
достигает максимума при .

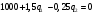Поэтому уравнение реакции фирмы I имеет следующий вид:



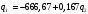
Прибыль фирмы II

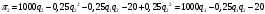достигает максимума при .

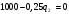Поэтому уравнение реакции фирмы 2 имеет следующий вид:

.

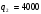Если фирмы ведут себя как равноправные конкуренты, то равновесные значения цены и объемов предложения определятся из следующей системы уравнений:

.

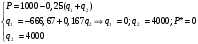Графическое решение представлено на рисунке 5.1.

2. 
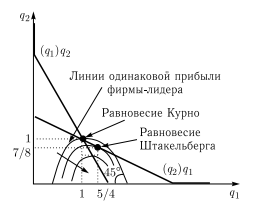
   Стратегия по Бертрану предполагает, что существует только одна цена, которая будет приносить максимальную прибыль каждому предприятию находящиеся в единой товарной нише.
   

В соответствии с данным условием решение задачи по Бертрану принимает вид:

Обе фирмы с самого начала назначают цену Р=МС, их совокупный выпуск (Q=q1+q2) как раз достаточен, чтобы удовлетворить отраслевой спрос.

В соответствии с моделью Бертрана q₁= q₂:

ТС=40-5/2Q².

Так как МС=5, то цена Р=МС=5.

Qd=1000-4Р, получаем Qd=1000-4*5=980.

Q= q₁+q₂

q₁ – объем производства первой фирмы

q₂ – объем производства второй фирмы

В соответствии с моделью Бертрана q₁= q₂:

q₁= q₂=980/2=490, q₁=490, q₂=490.

Графическое решение представлено на рисунке 5.2.

3. 
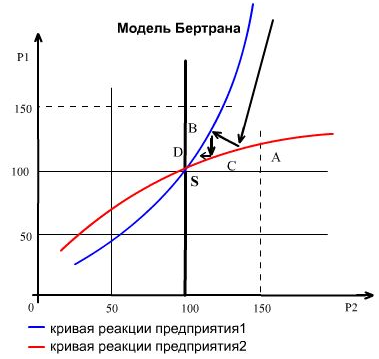
   Стратегия по Штакельбергу предполагает, что первый ход совершает лидер рынка. Он объявляет свое решение и стратегию поведения на рынке.
   

Решение задачи по сценарию Штакельберга принимает вид:

Пусть фирма II выступает в роли лидера, а фирма I – последователя. Тогда прибыль фирмы II с учетом уравнения реакции фирмы I будет:

---

.

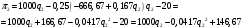
Она достигает максимума при 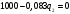. Отсюда

; ;

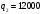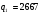P = 1000 – 0,25(12000-2667)=-2667.



Вывод: данная ситуация на рынке невозможна.

2. 
   График предельных издержек фирмы-монополиста задан условием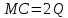 . Функция предельного дохода принимает вид: 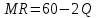. Определите эластичность рыночного спроса 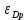при оптимальном выпуске фирмы-монополиста.
   

Решение

1. 
   Определяем оптимальный выпуск фирмы-монополиста:
   

MC=MR=Р;

2Q=60-2Q;

4Q=60;

Q=15.

2. 
   Выводим функцию спроса фирмы-монополиста:
   

P=a-bQ;

Исходя из MR b будет равно 1, а “а”=60.

Р=60-Q.

Q=60-P.

3. 
   Цена при оптимальном выпуске фирмы-монополиста составит Р=60-15=45.
   

Эластичность 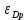в точке .

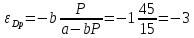Практическое задание 6

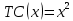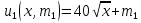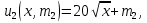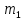Предположим, что издержки по вывозу мусора с территории двух районов составляют , где – площадь территории. Проведенные исследования выявили, что предпочтения всех жителей 1-го района принимают вид функции полезности , а предпочтения всех жителей 2-го района – где и 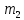– потребление агрегированного блага (вывоз мусора) всеми жителями соответствующих районов.

Найдите Парето-эффективное значение вывоза мусора с районов. Изобразите решение задачи на графике.

Решение

1. 
   Для определения Парето-эффективного значения вывоза мусора принимается условие, что  оптимальное количество площади определяется точкой пересече­ния линий предельных затрат MC = 2x и предельной общей полезности.
   
2. 
   Предельные издержки:
   

---

МС=ТС’=2x.

Общая полезность образуется в результате вертикального сложения графиков полезности:



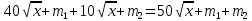
MU=25/ ;

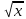MC=MU;

25/2= ;

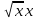x=5,39.

3. 
   В результате решения Парето-эффективное значение вывоза мусора составит 5,39.
   
4. 
   На рисунке 6 представлен график Парето-эффективности.
   

Список использованной литературы

1. 
   Носова С.С. Экономическая теория: Учебник для студентов, обучающихся по экономическим специальностям. - М.: ВЛАДОС, 2018. 406 с.
   
2. 
   Нуреев Р.М. Курс микроэкономики: Учебник для вузов. - 2-е изд., изм. - М.: Норма, 2020. 312 с.
   
3. 
   Тарануха Ю.В., Земляков Д.Н. Микроэкономика: Учебник / под. ред. проф., д.э.н. А.В. Сидоровича - М: Дело и Сервис, 2019. 606 с.
   
4. 
   Хорвард К. Эрнашвили Н.Д., Никитин А.М. Экономическая теория: Учебник для вузов. - 2-е изд., перераб и доп. - М.: ЮНИТИ-ДАНА, 2017. 398 с.
   
5. 
   Экономика: Учебник для вузов / Под ред. Е.Н. Лобачевой. - М.: Экзамен, 2018. 592 с.
   
6. 
   Экономическая теория (для эк. вузов): Учебник / под ред. О.С. Белокрыловой. - Ростов н/Д: Феникс, 2018. 448 с.
   
7. 
   Экономическая теория / С.В. Фомишин, С.В. Мочерний. - Ростов н/Д: Феникс, 2019. 509 с.
   
8. 
   Экономическая теория. Микроэкономика. Макроэкономика. Мегаэкономика. / под. ред. А.И. Добрынина, Л.С. Тарасевича: Учебник для вузов 3-е изд. СПб: Питер, 2020. 416 с.
   
9. 
   Экономическая теория: Учебное пособие для студентов неэкономических специальностей высших учебных заведений / Базылев Н.И., Базылева М.Н. - Мн.: Книжный дом, 2021. 321 с.
   

---