Файл: Лабораторная работа 6 Определение эйлеровых и гамильтоновых циклов графа.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 39
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа №6
Определение эйлеровых и гамильтоновых циклов графа.
Построить все его гамильтоновы циклы и цепи графа с использованием алгоритма Робертса и Флореса.
Варианты задания:
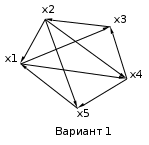
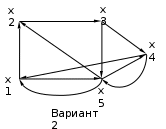
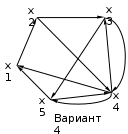
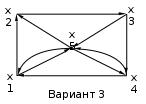
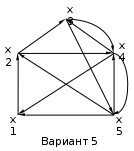
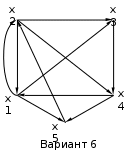
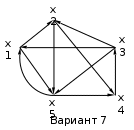
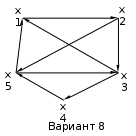
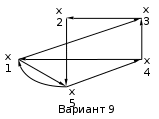
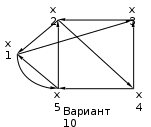
Методические указания по выполнению задания
Цикл (цепь) в графе G называется гамильтоновым (гамильтоновой), если он (она) проходит через каждую вершину графа ровно один раз. Граф называется гамильтоновым, если он содержит гамильтонов цикл.
Алгоритм Робертса и Флореса для построения гамильтонова цикла включает следующие шаги:
1. Строится матрица М с элементами mij, число строк в которой равно максимальной степени вершин графа, число столбцов равно количеству вершин n. Элемент mij - i-я вершина, (например xk) смежная с вершиной xj. Вершины в столбцах матрицы M упорядочены.
2. p = x1, где x1 - начальная вершина. S={x1}, где S - множество вершин строящегося гамильтонова цикла.
3. Если в столбце матрицы M, соответствующем вершине p, существует возможная вершина ( под возможной понимается вершина, ещё не принадлежащая S), то переход к шагу 4 , если нет, то переход к шагу 7.
4. В столбце, соответствующем вершине p, выбирается первая возможная вершина xk; эта вершина присоединяется к множеству S и p = xk.
5. Если мощность множества S равна |S| = n, то найдена гамильтонова цепь, переход к шагу 6, а если |S| < n, то переход к шагу 3.
6. Если существует дуга или ребро (p, x1), то найден гамильтонов цикл. Если надо найти все гамильтоновы циклы, то переход к шагу 7; иначе останов алгоритма.
7. Возвращение. Из множества S удаляется последняя включённая вершина xr. Если при этом S = (множество S пустое), то следует остановка алгоритма, т.е. все цепи и циклы найдены (или нет).
Если S, то p = xr-1, где (r-1) - номер вершины, включенной в гамильтонов цикл.
8. Если в столбце p существуют возможные вершины, т.е. вершины, следующие за xr, то переход к шагу 4. В противном случае xr = xr-1 и переход к шагу 7.
Пример Построить гамильтоновы цепи и циклы для графа
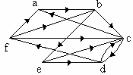
Решение. Матрица M приводится ниже, вершины в каждом столбце расположены в алфавитном порядке:
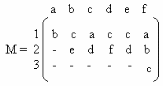
Поиск всех гамильтоновых циклов производится следующим образом (вершина a выбирается в качестве или начальной вершины):
Множество S Комментарии
1. a Добавляем первую возможную верши-
ну в столбце a (то есть вершину b).
2. a, b Добавляем первую возможную верши-
ну в столбце b (то есть вершину c).
3. a, b, c Первая вершина (a) в столбце с не
является возможной (aS), добавляем
следующую вершину в столбце
(то есть вершину d).
4. a, b, c, d Добавляем вершину f.
5. a, b, c, d, f В столбце f нет возможной вершины.
Возвращение.
6. a, b, c, d В столбце d не существует возможной
вершины , следующей за f.
Возвращение.
a, b, c Аналогично предыдущему.
Возвращение.
8. a, b Добавляем вершину e.
9. a, b, e Добавляем вершину c.
10. a, b, e, c Добавляем вершину d.
11. a, b, e, c, d Добавляем вершину f.
12. a, b, e, c, d, f Гамильтонов цикл, замыкающийся дугой
(f, a). Возвращение.
13. a, b, e, c, d Возвращение.
14. a, b, e, c Возвращение.
15. a, b, e Добавляем вершину d.
16. a, b, e, d Добавляем вершину f.
17. a, b, e, d, f Добавляем вершину c.
18. a, b, e, d, f, c Гамильтонов цикл, замыкающийся
дугой (c, a). Возвращение.
19. a, b, e, d, f Возвращение.
20. a, b, e, d Возвращение.
21. a, b, e Возвращение.
22. a, b Возвращение.
23. a Возвращение.
24. Конец поиска.