Файл: Лабораторная работа 4 Разработка программного обеспечения для определения метрических характеристик графа. Определение центра, радиуса, диаметра, медианы графа. Программная реализация минимаксных и минисуммных задач размещения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 23
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа №4
Разработка программного обеспечения для определения метрических характеристик графа. Определение центра, радиуса, диаметра, медианы графа. Программная реализация минимаксных и минисуммных задач размещения.
Методические указания по выполнению задания
Пусть G=(X,U) - связный граф, а
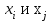- две его несовпадающие вершины. Длина кратчайшего маршрута, соединяющего вершины 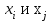(пути из 
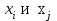) называется расстоянием между вершинами 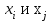и обозначается 
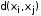. Положим 
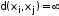, если вершины 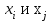не соединены маршрутом (путем). Расстояние 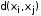удовлетворяет следующим аксиомам метрики:1)
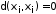;2)
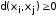;3)
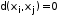тогда и только тогда, когда 
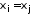;4)
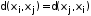для симметрических графов;5)
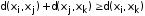(неравенство треугольника).Расстояние для графа G удобно задавать матрицей расстояний. Матрицей расстояний графа с n вершинами называется квадратная матрица D порядка n, элементы которой определяются следующим образом:
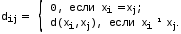
Матрицу расстояний можно определить
Для фиксированной вершины
величина 
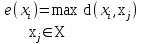
называется эксцентриситетом (отклоненностью) вершины
.Максимальный среди эксцентриситетов вершин называется диаметром графа G и обозначается diam (G):
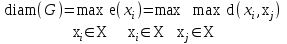
Минимальный из эксцентриситетов вершин связного графа называется его радиусом и обозначается через r(G):
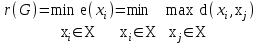
Вершина, имеющая минимальный эксцентриситет, называется центром графа.
Для вершины
число 
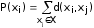называется передаточным числом. Вершина графа, которой соответствует минимальное передаточное число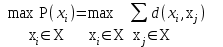
называется медианой графа. Центров и медиан в графе может быть несколько.
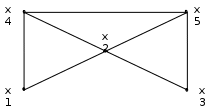
Рис. 1
Пример. Для графа, изображенного на рис.1 метрические характеристики определяются следующим образом:
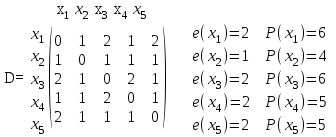
Радиус графа равен 1, диаметр равен 2. Центр графа - вершина
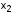; Медиана графа - вершина 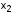.Определить метрические характеристики графа.
Варианты задания
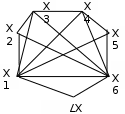
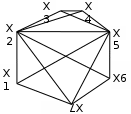
Вариант 1 Вариант 2
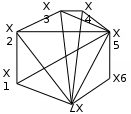
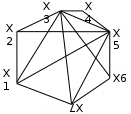
Вариант 3 Вариант 4
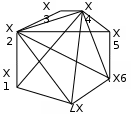
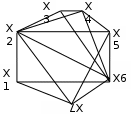
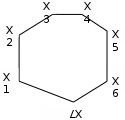
Вариант 5 Вариант 6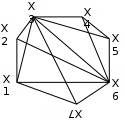
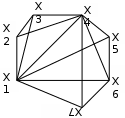
Вариант 7 Вариант 8
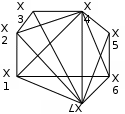
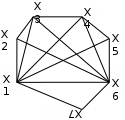
2. Определить сильные компоненты графа.
Варианты заданий
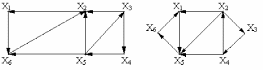
Вариант 1 Вариант 2
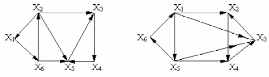
Вариант 3 Вариант 4
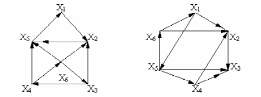
Вариант 5 Вариант 6
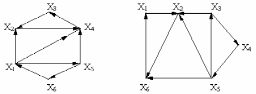
Вариант 7 Вариант 8
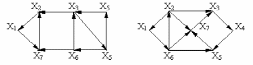
Вариант 9 Вариант 10
Методические указания по выполнению задания
Орграф называется сильно связным, если любые две его вершины взаимно достижимы, односторонне связным, если для любых двух вершин по крайней мере одна достижима из другой и слабо связным, если связным является лежащий в его основе неорграф.
Сильной компонентой орграфа называется его максимальный сильно связный подграф, подграф, не содержащийся ни в каком другом сильно связном подграфе этого графа.
Для определения сильных компонент графа необходимо:
1. Построить матрицу достижимости графа. Матрицей достижимости графа с n вершинами называется квадратная матрица R порядка n, элементы которой определяются следующим образом:
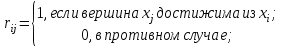
2. Построить матрицу контрдостижимости графа. Матрицей контрдостижимости графа с n вершинами называется квадратная матрица Q порядка n, элементы которой определяются следующим образом:
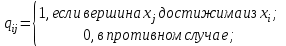
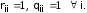
Матрицу контрдостижимости можно определить по матрице достижимости следующим образом:
3. Построить матрицу сильной связности графа. Матрицей сильной связности орграфа с n вершинами называется квадратная матрица S порядка n, элементы которой определяются следующим образом:
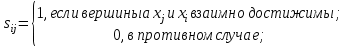
Матрицу сильной связности можно определить следующим образом:
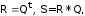
где * - операция поэлементного умножения матриц.
4. По матрице сильной связности выделить сильные компоненты графа. Если вершины
принадлежат одной сильной компоненте орграфа, то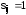 
. При этом строки (столбцы), соответствующие этим вершинам в матрице S, одинаковы. Пример
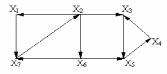
Для данного графа матрицы R, Q и S имеют вид:
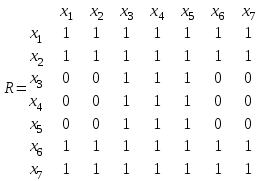
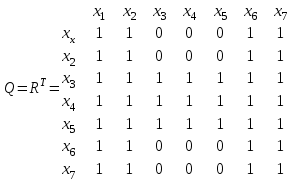
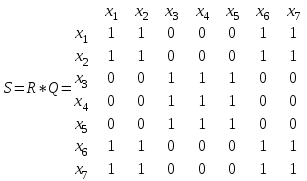
В соответствии с матрицей S сильные компоненты графа:
х1, х2, х6,х7 –первая сильная компонента;
х3, х4, х5 - вторая сильная компонента.