Файл: Вопросы по геометрии 8 класс Определение, свойства и признаки.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 03.12.2023

Просмотров: 30

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Вопросы по геометрии 8 класс
Определение, свойства и признаки


  1. Четырехугольник и его элементы (определение четырехугольника, сторон, вершин, понятие соседних, противолежащих вершин и сторон, сумма углов, виды четырехугольников с чертежами)

  2. Параллелограмм. Определение высоты параллелограмма. Свойства и признаки параллелограмма.

  3. Окружность. Касательная к окружности (взаимное расположение прямой и окружности, свойство и признак касательной)

  4. Прямоугольник. Свойства и признаки прямоугольника.

  5. Ромб. Свойства и признаки ромба.

  6. Квадрат. Свойства и признаки квадрата. Формула площади квадрата.

  7. Формулы площадей треугольников. Определение средней линии.

  8. Окружность. Теоремы о диаметре и хорде (основные определения, чертежи, формулировки теорем)

  9. Трапеция. Виды трапеции. Свойства равнобокой трапеции. Определение высоты трапеции. Формула площади трапеции. Средняя линия трапеции

  10. Центральные и вписанные углы окружности. Свойства вписанных углов.

  11. Описанная и вписанная окружности четырехугольника.

  12. Теорема Фалеса, теорема о пропорциональных отрезках, теорема о медианах (формулировки)

  13. Подобные треугольники (определение и лемма)

  14. Тригонометрические функции острого угла прямоугольного треугольника. Основное тригонометрическое тождество, формулы приведения. Таблица значений.

  15. Многоугольники (определение вершин, сторон, понятие соседних вершин и сторон, выпуклый многоугольник, его свойства). Понятие площади многоугольника, свойства его площади, определение равновеликих многоугольников

  16. Угол между касательной и хордой. Угол между пересекающимися хордами. Угол между непересекающимися хордами.


Доказать


  1. Теорема о сумме углов четырёхугольника

  2. Формула площади параллелограмма

  3. Теорема о двух касательных из одной точки.

  4. Признаки прямоугольника

  5. Признаки ромба

  6. Доказать, что середины сторон четырехугольника являются вершинами параллелограмма.

  7. Теорема о средней линии треугольника с доказательством

  8. Формула площади трапеции

  9. Теорема о градусной мере вписанного угла с доказательством.

  10. Свойства вписанного и описанного четырехугольников с доказательством.

  11. Теорема о свойстве биссектрисы с доказательством

  12. Доказать, что отношение периметров подобных треугольников равно коэффициенту подобия.

  13. Первый признак подобия треугольников с доказательством (по двум углам).

  14. Свойства пересекающихся хорд, свойства касательной и секущей с доказательствами.

  15. Второй и третий признак подобия треугольников (по двум сторонам и углу между ними и по трем сторонам).

  16. Теорема Пифагора с доказательством


Задачи (базовый уровень)

  1. Чему равен четвёртый угол четырёхугольника, если три его угла равны 500, 700 и 1300


  2. Точки M,K,N – середины сторон треугольника АВС. Периметр треугольникаMKN равен 16 см. Чему равен периметр треугольника АВС?

  3. Сумма трёх углов равнобокой трапеции равна 2200. Найдите углы трапеции.


  4. Периметр равнобокой трапеции равен 26 см, а боковая сторона – 6 см. Чему равна средняя линия трапеции?

  5. Чему равна градусная мера центрального угла окружности, опирающегося на дугу, которая составляет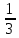 окружности.

  6. Чему равна градусная мера вписанного угла окружности, опирающегося на дугу, которая составляет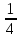 окружности.

  7. Найдите неизвестные углы вписанного четырёхугольника, если два его угла равны 360 и 1450.

  8. Боковые стороны трапеции, описанной около окружности, равны12 см и 26 см. Найдите среднюю линию трапеции

  9. Треугольник АВС подобен треугольнику А1В1С1 с коэффициентом подобия, равным 1,5. Стороны треугольника А1В1С1 равны 25 см, 20 см и 15 см. Найдите периметр треугольника АВС.

  10. Чему равна высота прямоугольного треугольника, проведённая к гипотенузе, если проекции катетов на гипотенузу равны 2 см и 72 см

  11. В треугольнике АВС с прямым углом С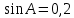 . Чему равен cos В

  12. Чему равен катет прямоугольного треугольника, гипотенуза которого равна 10 см, а прилежащий к искомому катету острый угол – 450.

  13. Сколько сторон имеет выпуклый многоугольник, сумма углов которого равна 12600

  14. Чему равна площадь параллелограмма, сторона которого равна 12 см, а проведённая к ней высота – 50 мм

  15. Найдите площадь прямоугольного треугольника, катеты которого равны 20 см и 30 см


  16. Чему равна площадь трапеции, основания которой равны 7 см и 8 см, а высота – 6 см?

Задачи повышенной сложности




  1. Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите диаметр окружности, если АВ=6, АС=10.

  2. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК=12, СК=16.

  3. На стороне AD параллелограмма ABCD отметили точку М. Найдите площадь параллелограмма, если площадь треугольника МВС равна 7.

  4. Около трапеции АВСD, один из углов которой равен 36°, описана окружность. Найдите остальные углы трапеции.

  5. Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.

  6. Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках К и М соответственно. Найдите АС, если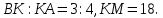

  7. Отрезки АВ и СD являются хордами окружности. Найдите длину хорды CD, если АВ=40, а расстояние от центра окружности до хорд АВ и CD равны соответственно 21 и 20.

  8. На сторонах АВ и ВС треугольника АВС взяты соответственно точки М и N так, что угол BMN равен угла BCA. Найдите MN, если АС=28, АВ=21, ВN=15

  9. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 84°? Ответ дайте в градусах

  10. В треугольнике АВС угол С равен 90°,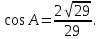 Найдите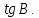

  11. Окружность, вписанная в треугольник АВС, касается его сторон в точках M, N, Р. Найдите углы треугольника АВС, если углы треугольника MNP равны 52°, 56° и 72°.

  12. Точка H является основанием высоты BH, проведённой из вершины прямого угла В прямоугольного треугольника АВС. Окружность с диаметром BH пересекает стороны АВ и СВ в точках Р и К соответственно. Найдите ВН, если РК=15.

  13. Отрезки АВ и CD лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ=15, DC=30, АС=39.

  14. Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF=21, BF=20

  15. Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30° и 120°, а CD=25.

  16. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68. Найдите углы ромба.

  17. Катеты прямоугольного треугольника равны 15 и 36. Найдите высоту, проведенную к гипотенузе

  18. Угол, противолежащий основанию равнобедренного треугольника, равен 120°, а высота, проведенная к боковой стороне, равна 8 см. Найдите основание треугольника

  19. Диагональ трапеции перпендикулярна её основаниям, тупой угол, прилежащий к большему основанию, равен 120°, боковая сторона, прилежащая к этому углу,-12 см, а большее основание -16 см. Найдите среднюю линию трапеции.

  20. Найдите углы параллелограмма, если угол между его высотами, проведенными из одной вершины, равен 130°

  21. Один из углов прямоугольной трапеции равен 135°, средняя линия -21 см, а основания относятся как 5 : 2. Найдите меньшую боковую сторону трапеции.

  22. В трапеции ABCD известно, что угол В равен 90°, угол С равен 150°, ВС=5 см. Найдите сторону CD, если высота трапеции, проведённая из вершины С, разбивает данную трапецию на треугольник и квадрат.

  23. Биссектрисы углов А и В параллелограмма ABCD пересекаются в точке М, АВ=6см. Найдите радиус окружности, которая проходит через точки А, В, М

  24. Периметр параллелограмма равен 48 см. Биссектриса тупого угла делит его сторону в отношении 2 : 1, считая от вершины острого угла. Может ли меньшая сторона параллелограмма быть равной 7 см?

  25. В равнобокой трапеции диагональ является биссектрисой тупого угла и делит среднюю линию трапеции на отрезки длиной 7 см и 11 см. Найдите периметр трапеции

  26. Медиана и высота прямоугольного треугольника, проведённые к гипотенузе, равны соответственно 13 см и 12 см. Найдите периметр данного треугольника

  27. В равнобедренном треугольнике АВС с основанием АС медианы АМ и СК пересекаются в точке О. Докажите, что треугольник АОС – равнобедренный, и найдите его боковые стороны, если АМ=21 см.

  28. В равнобокой трапеции основания равны 18 см и 12 см. Боковая сторона образует с основанием угол 30°. Найдите диагональ трапеции.

Смотрите также файлы