Файл: Белорусский государственный университет факультет радиофизики и компьютерных технологий.docx

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ФАКУЛЬТЕТ РАДИОФИЗИКИ И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ

Кафедра физики и аэрокосмических технологий

КВАНТОВЫЕ КОМПЬЮТЕРЫ

Реферат

Дуньчик Алёны Игоревны

Студентка 2 курса 4 группы

Минск 2021

Оглавление

Введение

Цифровые электронные компьютеры, широко используемые в настоящее время, созданы с помощью полупроводниковых технологий. Такие компьютеры обычно представляют собой совокупность элементов только с двумя возможными логическими состояниями «0» и «1» — так называемыми «битами». Такие компьютеры, в которых логические операции производятся с этими классическими, с точки зрения физики, состояниями в настоящее время принято называть классическими.

Однако уже достаточно давно было обнаружено, что эти классические компьютеры не могут справиться с некоторыми очень важными задачами. Примерами таких задач являются поиск в неструктурированной базе данных, моделирование эволюции квантовых систем (например, ядерные реакции) и, наконец, факторизация больших чисел.

Интерес к последней задаче связан с тем, что практически все современные шифры для секретной переписки основаны на этой математической процедуре. Для взлома уже существующего кода необходима работа классического компьютера в течение нескольких лет.

Идея квантовых вычислений впервые была высказана Ю.И. Маниным [1] в 1980 году, но активно эта проблема стала обсуждаться после появления в 1982 году статьи американского физика-теоретика Р. Фейнмана [2]. В этих работах было предложено использовать для вычислений операции с состояниями квантовой системы. Авторы обратили внимание на то, что каждое состояние квантовой системы в отличие от классической может находиться в состоянии суперпозиции. В терминах классического компьютера квантовый бит, или кубит, в соответствии с законами квантовой механики может находиться одновременно в состоянии «0» и «1».

Наиболее популярная попытка объяснения этой «странности» квантового мира производится на примере свойства спина электрона, ярко проявляющегося в экспериментах ядерного магнитного резонанса (ЯМР). Это свойство электрона часто изображают в виде вращения волчка с осью вращения, направленной вверх или вниз. Спин вверх можно принять за единицу, спин вниз за ноль. Но оказывается можно показать математически, что электрон может также находиться в «призрачном» двойном состоянии, состоянии суперпозиции, в котором спин как бы смотрит одновременно вверх и вниз. Это означает, что такое состояние есть одновременно ноль и единица. Если теперь выполнять вычисление с помощью этого электрона, то они будут выполняться с одновременным использованием нуля и единицы!

Поскольку данная работа имеет реферативный характер, то основной её целью является знакомство с основными знаниями и понятиями на таком уровне, что человек, не имеющий никакого понятия о квантовых вычислениях и квантовых компьютерах, но имеющий определённую математическую подготовку, после ознакомления с ней мог свободно читать научную литературу, посвящённую этому вопросу.

В первом разделе рассмотрена сама идея квантовых вычислений и её история, а также алгоритмы факторизации чисел и поиска в неупорядоченной базе данных. Второй раздел посвящён реализации квантовых компьютеров и основным направлениям развития их элементной базы.

Предпосылки создания квантовых компьютеров

Уже сейчас существует множество систем, в работе которых квантовые эффекты играют существенную роль. Одним из наиболее известных примеров может служить лазер: поле его излучения порождается квантово-механическими событиями - спонтанным и индуцированным излучением света. Другим важным примером таких систем являются современные микросхемы - непрерывное ужесточение проектных норм приводит к тому, что квантовые эффекты начинают играть в их поведении существенную роль. В диодах Ганна возникают осцилляции электронных токов, в полупроводниках образуются слоистые структуры: электроны или дырки в различных запертых состояниях могут хранить информацию, а один или несколько электронов могут быть заперты в так называемых квантовых ямах.

Сейчас уже существует новый класс квантовых устройств - квантовых компьютеров, которые с каждым годом увеличивают свою мощность. Идея квантового компьютера возникла так.

Все началось в 1982 году, когда Фейнман [2] написал очень интересную статью, в которой рассмотрел два вопроса. Он подошел к процессу вычисления как физик: есть чисто логические ограничения на то, что можно вычислить (можно придумать задачу, для которой вообще нет алгоритма, можно придумать задачу, для которой любой алгоритм будет долго работать). А есть ли ограничения физические? Вот есть закон сохранения энергии - вечный двигатель невозможен; а есть ли какое-нибудь физическое ограничение на функционирование компьютера, которое накладывает некие запреты на реализуемость алгоритмов? И Фейнман показал, что термодинамических ограничений, типа второго начала термодинамики, нет. Если мы будем уменьшать потери энергии, шумы, то мы можем сделать сколь угодно длинные вычисления со сколь угодно малыми затратами энергии. Это означает, что вычисления можно сделать обратимым образом - потому что в необратимых процессах энтропия возрастает. Собственно, Фейнмана это и заинтересовало: ведь реальное вычисление на реальном компьютере необратимо. И полученный им результат состоит в том, что можно так переделать любое вычисление - без особой потери эффективности, - чтобы оно стало обратимым. Те вычисления, которые делаются «просто так», конечно, необратимы, но «рост необратимости» пренебрежимо мал по сравнению, скажем, с шумами в современном компьютере. То есть необратимость — это тонкий эффект; тут вопрос не практический, а принципиальный: если представить себе, что технология дойдет до такого уровня, что этот эффект станет существенным, то можно так перестроить вычисления, чтобы добиться обратимости.

И в этой же работе Фейнман обратил внимание на то, что если у нас имеется устройство квантовое, то есть подчиняющееся законам квантовой механики, то его вычислительные возможности совершенно не обязательно должны совпадать с возможностями обычного устройства. Возникают некоторые дополнительные возможности. Но пока непонятно, позволяют они получить какой-то выигрыш или нет. Фактически, он и поставил своей статьей такой вопрос.

Кстати, Ю.И. Манин в конце семидесятых годов написал две популярные книжки по логике - «Вычислимое и невычислимое» и «Доказуемое и недоказуемое», и в одной из них есть сюжет про квантовые автоматы, где он говорит о некоторых кардинальных отличиях этих автоматов от классических.

В середине восьмидесятых годов появились работы Дойча (D. Deutsch), Бернштейна и Вазирани (Е. Bernstein, U. Vazirani), Яo (A. Уао). В них были построены формальные модели квантового компьютера - например, квантовая машина Тьюринга [3-6].

Следующий этап - статья Шора (Р.W. Shor) [7] 1994 года, вызвавшая лавинообразный рост числа публикаций о квантовых вычислениях. Шор построил квантовый (то есть реализуемый на квантовом компьютере) алгоритм факторизации (разложения целых чисел на множители - используется в том числе для вскрытия зашифрованных сообщений). Все известные алгоритмы для обычного компьютера - экспоненциальные (время их работы растет как экспонента от числа знаков в записи факторизуемого числа). Факторизация 129-разрядного числа потребовала 500 MIPS-лет, или восемь месяцев непрерывной работы системы из 1600 рабочих станций, объединенных через Интернет. А при числе разрядов порядка 300 это время существенно превзойдет возраст Вселенной - даже если работать одновременно на всех существующих в мире машинах. Считается (хотя это и не доказано!), что быстрого алгоритма решения этой задачи не существует. Более того, гарантией надежности большинства существующих шифров является именно сложность решения задачи факторизации или одной из родственных ей теоретико-числовых задач, например - дискретного логарифма. И вдруг выясняется, что на квантовом компьютере эта задача имеет всего лишь кубическую сложность! Перед квантовым компьютером классические банковские, военные и другие шифры мгновенно теряют всякую ценность. Короче говоря, работа Шора показала, что вся эта изысканная академическая деятельность непосредственно касается такой первобытной стихии, как деньги. После этого и началась настоящая популярность...

Впрочем, выясняется, что не только классическая, но и квантовая криптография (наука о шифровании сообщений) часто не способна противостоять квантовой криптоаналитике (науке о расшифровке). Некоторые важные криптографические протоколы, такие как «подбрасывание монеты по телефону», рушатся при переходе к квантовым вычислениям. Точнее, гарантией их надежности является отныне не сложность тех или иных алгоритмов, а сложность задачи создания квантового компьютера.

Таким образом возникает новая отрасль вычислений – квантовые вычисления. Квантовые вычисления (КВ) — это, как можно догадаться, вычисления на квантовом компьютере. Тем не менее, квантовые вычисления - предмет, чрезвычайно модный сейчас в математике и физике, как теоретической, так и экспериментальной, и занимается им довольно много людей. Судя по всему, именно интерес стимулировал первопроходцев - Ричарда Фейнмана, написавшего пионерскую работу, в которой ставился вопрос о вычислительных возможностях устройств на квантовых элементах; Дэвида Дойча, формализовавшего этот вопрос в рамках современной теории вычислений; и Питера Шора, придумавшего первый нетривиальный квантовый алгоритм.

Благодаря этом открытиям началось стремительно развитие квантовых вычислений. В 2000 году продемонстрирован первый работающий пяти кубитный квантовый компьютер в Мюнхенском техническом университете. 2007 канадская компания D-WAVE продемонстрировала первый 16-кубитный и 28-кубитный квантовый компьютер. В 2011 году они выпустили квантовый компьютер с 128-битным чипом. В 2013 с 512-битным чипом. На самом деле эти компьютеры способны справится только с одной определенной задачей. Из-за этого на данный момент самым мощным квантовым компьютером считается 51-кубитный квантовый компьютер, который разработали русские ученые в 2017 году.

Типы квантовых компьютеров

Строго говоря, можно выделить два типа квантовых компьютеров. И те, и другие основаны на квантовых явлениях, только разного порядка.

Представителями первого типа являются, например, компьютеры, в основе которых лежит квантование магнитного потока на нарушениях сверхпроводимости - Джозефсоновских переходах. На эффекте Джозефсона уже сейчас делают линейные усилители, аналого-цифровые преобразователи, СКВИДы и корреляторы. Известен проект создания RISC-процессора на RSFQ-логике (Rapid Single Flux Quantum). Эта же элементная база используется в проекте создания петафлопного (1015 оп./с) компьютера. Экспериментально достигнута тактовая частота 370 ГГц, которая в перспективе может быть доведена до 700 ГГц. Однако время расфазировки волновых функций в этих устройствах сопоставимо со временем переключения отдельных вентилей, и фактически на новых, квантовых принципах реализуется уже привычная нам элементная база - триггеры, регистры и другие логические элементы.

Другой тип квантовых компьютеров, называемых еще квантовыми когерентными компьютерами, требует поддержания когерентности волновых функций используемых кубитов в течение всего времени вычислений - от начала и до конца (кубитом может быть любая квантомеханическая система с двумя выделенными энергетическими уровнями). В результате, для некоторых задач вычислительная мощность когерентных квантовых компьютеров пропорциональна 2N , где N - число кубитов в компьютере. Именно последний тип устройств имеется в виду, когда говорят о квантовых компьютерах.

Математические основы функционирования квантовых компьютеров

Рис. 1 Схема квантового бита - кубита
К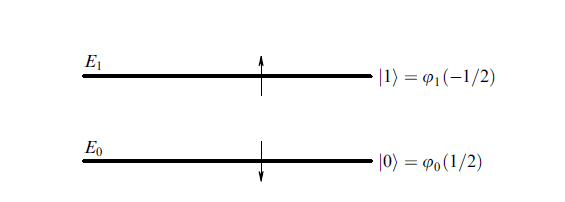
лассический компьютер состоит, грубо говоря, из некоторого числа битов, с которыми можно выполнять арифметические операции. Обычный бит — это классическая система, у которой есть только два возможных состояния. Можно сказать, что пространство состояний бита — это множество из двух элементов, например, из нуля и единицы.
Базовым элементом квантового компьютера (носителем квантовой информации) является квантовый бит – кубит. В системах квантовой связи информация передаётся путём физического переноса кубита – носителя информации – или методом телепортации квантового состояния кубита.
В качестве кубита может быть выбрана любая квантовая система с двумя состояниями, характеризуемыми ортонормированными волновыми функциям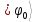и и 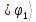. Удобным примеров кубита являются ядерные (или электронные) спины 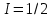, которые в постоянном внешнем магнитном поле B имеют два уровня энергии:

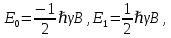соответствующих направлениям спина вдоль поля или против поля (рис. 1).

Волновые функции 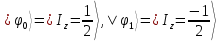являются собственными функциями оператора полной энергии спина в магнитном поле B:
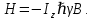[8]

Система является квантовой, поэтому ей пространство будет намного богаче.
Математически кубит — это двумерное комплексное пространство.

В такой системе можно выполнять унитарные преобразования пространства состояний системы. С точки зрения геометрии такие преобразования - прямой аналог вращении и симметрий обычного трехмерного пространства. Согласно принципу суперпозиции вы можете складывать состояния, вычитать их, умножать на комплексные числа. Эти состояния образуют фазовые пространства. При объединении двух систем полученное фазовое пространство будет их тензорным произведением. Эволюция системы в фазовом пространстве описывается унитарными преобразованиями фазового пространства.

Так вот, в квантовом компьютере аналогичная ситуация. Он тоже работает с нулями и единицами. Но его функциональные элементы реализуют действия прямо в фазовом пространстве некоторой квантовой системы при помощи унитарных преобразований этого пространства.

Конечно, унитарные преобразования не могут быть произвольными - они должны удовлетворять некоторым естественным ограничениям. Например, в случае обычной логики достаточно иметь три операции: конъюнкция, дизъюнкция, отрицание. Все можно реализовать, используя только эти три операции. Точно так же и в квантовом случае есть некоторый набор операторов, действующих только на три бита, с помощью которых можно все реализовать. Там есть даже более тонкие результаты: можно ограничиться классическими операторами на нескольких битах, а квантовые операторы будут действовать только на один бит. То есть классический набор операций {конъюнкция, дизъюнкция, отрицание} можно заменить на такой: {конъюнкция, дизъюнкция, квантовое отрицание}, где квантовое отрицание - это произвольное унитарное преобразование одного кубита.

Фазовое пространство квантовых компьютеров есть тензорное произведение кубитов. Если в каждом кубите фиксирован базис (он будет состоять из двух векторов), то фазовое пространство - это комплексное линейное пространство, базис которого индексирован словами из нулей и единиц. Таким способом двоичное слово на входе определяет базисный вектор.

Итак, вход - двоичное слово, определяющее один из базисных векторов. Сам же алгоритм - предписанная последовательность элементарных операторов. Применяем эту последовательность к вектору на входе, в результате получаем некоторый вектор на выходе.

Так вот, согласно квантовой механике (КМ), пока система эволюционирует под действием наших унитарных операторов, мы не можем сказать, в каком именно классическом состоянии она находится. То есть она находится в каком-то квантовом состоянии, но измеряем-то мы, когда общаемся с системой, все равно какие-то классические значения. Как это понимается в квантовой механике? В фазовом пространстве фиксируется некоторый базис, и вектор состояния разлагается по этому базису. Это математическая формализация процедуры измерения в КМ. То есть если мы имеем дело с системой, у которой «то ли спин влево, то ли спин вправо», и если мы все-таки посмотрим, какой спин, то мы получим одно из двух в любом случае. А вот вероятности того, что мы получим тот или другой результат, - это как раз квадраты модуля коэффициентов разложения. Квантовая механика утверждает, что точно предсказать результат измерения нельзя, но вероятности возможных результатов вычислить можно.

Вероятность возникает в процессе измерения. А пока система живет, для нас существенно, что там есть сам этот вектор.

Другими словами, существенно, что система «находится одновременно во всех возможных состояниях». Как пишут многие авторы популярных введений в квантовые вычисления, возникает совершенно чудовищный параллелизм вычислении: к примеру, в случае нашей системы из двух кубитов мы как бы оперируем одновременно со всеми возможными ее состояниями: 00, 01, 11, 10.

Чтобы интерпретировать ответ, надо заранее условиться, что какой-то бит - допустим, первый - это бит ответа. Пусть алгоритм проработал, у нас получился какой-то вектор, не обязательно базисный. Тогда мы можем сказать, что первый бит с некоторой вероятностью равен 1. И требование к алгоритму такое: если ответ «да», то вероятность того, что первый бит равен 1, должна быть больше двух третей. А если ответ «нет», вероятность того, что будет ноль, должна быть тоже больше двух третей.

Задачи, реализуемые на КВ

Известно два примера нетри­виальных задач, в которых KB дают радикальный выигрыш.

Первый из них - задача разло­жения целых чисел на простые мно­жители и, как следствие, вычисле­ния дискретного логарифма (ДЛ). Дальше речь пойдет именно о ДЛ.

Пусть у нас есть поле вычетов по модулю простого числа. В нем есть первообразные корни - такие вы­четы, чьи степени порождают все ненулевые элементы. Если задан такой корень и задана степень, то возвести в степень можно быстро (например, сначала возводим в квадрат, потом получаем четвертую сте­пень, и т. д.) Дискретный лога­рифм - это обратная задача. Дан первообразный корень и какой-то элемент поля; найти, в какую степень нужно возвести этот корень, чтобы получить данный элемент. Вот эта задача уже считается сложной. На­столько сложной, что ряд совре­менных криптографических систем основан на том предположении, что вычислить ДЛ за приемлемое время невозможно, если модуль - доста­точно большое простое число.

Так вот, для дискретного лога­рифма есть эффективный кванто­вый алгоритм. Его придумал Шор в конце 1994 года. Пос­ле его статьи и начался взрыв публи­каций по КВ. Независимо от него, Алексей Китаев из ИТФ им. Ландау построил квантовый алгоритм для этой и некоторых более общих за­дач [9]. Идеи у них были разные.

Шор использовал примерно такую идею, она существенно квантовая: рассмот­рим базис в фазовом пространстве. Он состоит из классических состояний. Но в линейном пространстве много базисов. Мы можем найти некий оператор, который эффективно строит другой базис; мы можем к нему перейти, сделать там какие-то вычисления, вернуться обратно и получить нечто совершенно отлич­ное от того, что мы имели бы в классическом базисе. Одна из воз­можностей использовать квантовость состоит в том, что мы строим какой-то странный базис, в нем что-то делаем, возвращаемся обратно и интерпретируем результат. Шор именно эту идею и реализовал. При­чем преобразование оказалось та­кое, которое и в физике, и в матема­тике имеет принци­пиальное значение - дискретное преобразование Фурье.

Его можно представить в виде тензорного произведения опера­торов, которые действуют на каж­дый из кубитов такой матрицей:



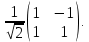
Китаев придумал примерно следующее. Есть некото­рая ячейка - основной регистр, где мы записываем наши данные нулями и единицами. И еще есть один управляющий кубит. Мы ра­ботаем так: у нас реализована про­цедура умножения на первообраз­ный корень, на квадрат первооб­разного корня, и т. д. Управляю­щий кубит переводим в некоторое смешанное состояние, дальше строим такой оператор, который, в зависимости оттого, ноль или еди­ница в этом управляющем кубите, либо применяет умножение к на­шему основному регистру, либо не применяет. А потом кубит опять возвращаем в смешанное состоя­ние. Оказывается, что это эффек­тивный способ проделать некото­рое измерение. То есть Китаев за­метил, что одна из вещей, которые мы можем эффективно делать на квантовом компьютере, - это имитировать процесс квантового измерения. В данной задаче из результатов этих измерений эф­фективно извлекается ответ.

Сам процесс вычислений, происходит так: мы все время умножаем одну и ту же ячей­ку на некие константы, результаты измерений записываем, а потом производим своего рода обработ­ку результатов эксперимента - уже чисто классическими вычис­лениями. Вся квантовая часть зак­лючается в том, что где-то рядом с нашим регистром находится в некоем смешанном состоянии коррелированный с ним кубит, и мы его периодически наблюдаем.

Для вы­числения ДЛ числа, записанного N битами, нужно потратить N ³еди­ниц времени. Вполне реализуе­мо - на КК, естественно. Но здесь надо заметить, что никто пока не доказал, что не существует столь же быстрого алгоритма для вы­числения ДЛ на обычной машине.

Вторая задача предложена Гровером (L. Grover) [10]. Рассмотрим базу дан­ных, содержащую 2^Nзаписей. Мы хотим найти ровно одну запись. Имеется некая процедура опреде­ления того, нужную запись мы взяли или нет. Записи не упоря­дочены. С какой скоростью мы можем решить эту задачу на обыч­ном компьютере? В худшем слу­чае нам придется перебрать все 2^Nзаписей - это очевидно. Оказывается, что на КК достаточно числа запросов по­рядка корня из числа записей – 2^N/2 .

Интересная задача - созда­ние оптимальных микросхем. Пусть есть функция, которую нужно ре­ализовать микросхемой, и эта функция задана программой, ис­пользующей полиномиально ог­раниченную память. Построение нужной микросхемы с минималь­ным числом функциональных эле­ментов - задача PSPACE. По­этому появление устройств, эф­фективно решающих PSPACE-задачи, позволило бы единообразно проектировать оптимальные по своим показателям вычислитель­ные устройства обычного типа. Кроме того, в PSPACE попадает большинство задач «искусственного интеллекта»: машинное обучение, распознавание образов и т.д.

Так вот, точно установлено, что KB находятся где-то между обыч­ными вероятностными вычисле­ниями и PSPACE. Если все же ока­жется, что KB можно эффективно реализовать на классических ве­роятностных машинах, не будет смысла в физической реализации квантовых машин. Если же выяс­нится, что при помощи KB можно эффективно решать те или иные PSPACE-задачи, то физическая реализация КК откроет принци­пиально новые возможности.

Есть еще одна область применения КК, где заведомо возможен радикальный выигрыш у существующих техно­логий. Это моделирование самих квантовых систем.

Давайте посмотрим на такой вопрос: как можно эволюцию квантовой системы изучать на обычном компьютере? Это посто­янно делается, так как это задача важна для химии, молеку­лярной биологии, физики и т.п. Но, за счет эк­споненциального роста размер­ности при тензорном произведе­нии, для моделирования десяти спинов вам нужно оперировать с тысячемерным пространством, сто спинов - это уже конец. А если вспомнить, что в молекуле белка десятки тысяч атомов, то... Там, правда, не всюду существенно именно квантовое моделирование, но в целом ясно, что есть очень серьезные препятствия для моде­лирования квантовых систем на классических компьютерах. Так что если создать вычислительное устройство, которое ведет себя квантовым образом, то по край­ней мере один важный класс за­дач на нем есть смысл решать - можно моделировать реальные квантовые системы, возникающие в физике, химии, биологии.

Проблемы создания КК

Когда начался бум вокруг квантовых вычислений, физики высказывались об этом бо­лее чем скептически. Модель кван­товых вычислений не противоре­чит законам природы, но это еще не значит, что ее можно реализовать. К примеру, можно вспомнить создание атом­ного оружия и управляемый термояд.

А если говорить о КК, надо отме­тить одну очень серьезную пробле­му. Дело в том, что любая физичес­кая реализация будет приближен­ной. Во-первых, мы не сможем сде­лать прибор, который будет давать нам произвольный вектор фазово­го пространства. Во-вторых, работа любого устройства подвержена вся­ческим случайным ошибкам. А уж в квантовой системе - пролетит ка­кой-нибудь фотон, провзаимодействует с одним из спинов, и все поменяется. Поэтому сразу возник вопрос, можно ли, хотя бы в прин­ципе, организовать вычисления на ненадежных квантовых элементах, чтобы результат получался со сколь угодно большой достоверностью. Такая задача для обычных компью­теров решается просто - напри­мер, за счет введения дополнитель­ных битов.

В случае КК эта проблема го­раздо глубже. То место, где воз­никает новое качество KB по срав­нению с обычными вычисления­ми, - это как раз сцепленные состояния - ли­нейные комбинации базисных век­торов фазового пространства. У вас есть биты, но они не сами по себе живут в каких-то состояниях - это был бы просто вероят­ностный компьютер (компьютер, дающий тот или иной ответ с определенной вероятностью), - а они на­ходятся в некоем смешанном со­стоянии, причем согласованно-смешанном. Из-за этого в КК нельзя, например, просто взять и скопировать один бит в другой! Обычная интуиция из теории алгоритмов здесь неприменима.

Так что проблема надежности довольно сложна, даже на уровне чистой теории. Те люди, которые активно занимаются KB, активно ее решали и добились успеха: доказано, что, как и в классике, можно делать вычисления на элементах с за­данной надежностью сколь угод­но точно. Это реализовано с по­мощью некоего аналога кодов, ис­правляющих ошибки.

Что касается технической сто­роны появляются сообщения, что созда­ются реальные квантовые систе­мы с небольшим числом битов - с двумя, скажем. Эксперименталь­ные, в железе, так сказать.

Так что эксперименты есть, но пока очень далекие от реальнос­ти. Два бита - это и для класси­ческого и для квантового компь­ютера слишком мало! Чтобы мо­делировать молекулу белка, нуж­но порядка ста тысяч кубитов. Для ДЛ, чтобы вскрывать шифры, достаточно примерно тысячи кубитов.

Задача эта возникла слишком недавно, и не исключено, что она потребует каких-то фундаменталь­ных исследований в самой физи­ке.

Но можно ожидать распрост­ранения через не очень долгое время квантовых криптографи­ческих систем. Квантовая крип­тография позволяет обмениваться сообщениями так, что враг, если попытается подслушать, сможет разве что разрушить ваше сооб­щение. То есть оно не дойдет до адресата, но перехватить его в принципе будет нельзя. Подобные системы, кото­рые уже реализованы, используют све­товод. Универсальный КК здесь не нужен. Нужно специа­лизированное квантовое устрой­ство, способное выполнять только небольшой набор операций, - сво­его рода квантовый кодек.

Физической системе, реализующей квантовый компьютер, можно предъявить пять требований:

1. 
   Система должна состоять из точно известного числа частиц.
   
   
2. 
   Должна быть возможность привести систему в точно известное начальное состояние.
   
   
3. 
   Степень изоляции от внешней среды должна быть очень высока.
   
   
4. 
   Надо уметь менять состояние системы согласно заданной последовательности унитарных преобразований ее фазового пространства.
   
   
5. 
   Необходимо иметь возможность выполнять «сильные измерения» состояния системы (то есть такие, которые переводят ее в одно из чистых состояний).
   

Из этих пяти задач наиболее трудными считаются третья и четвертая. От того, насколько точно они решаются, зависит точность выполнения операций. Пятая задача тоже весьма неприятна, так как измерить состояние отдельной частицы нелегко.

Физические основы организации КК

Итак, что же это за тайное оружие такое - КК? Остроумная идея за­ключается в использовании для хра­нения, передачи и обработки ин­формации существенно квантовых свойств вещества. В основном такие свойства проявляют объекты мик­ромира: элементарные частицы, атомы, молекулы и небольшие сгу­стки молекул, так называемые кла­стеры. (Хотя, конечно, и в жизни макромира квантовая механика иг­рает важную роль. В частности, только с ее помощью можно объяснить та­кое явление, как ферромагнетизм.) Одним из квантовых свойств веще­ства является то, что некоторые ве­личины при измерении (наблюде­нии) могут принимать значения лишь из заранее определенного дискрет­ного набора. Такой величиной, на­пример, является проекция собст­венного момента импульса, или, ина­че говоря, спина элементарной час­тицы, на любую заданную ось. На­пример, у электрона возможно только два значения проекции: +1/2 или –1/2 . Таким образом, количество информации, необходимое для со­общения о проекции, равно одному биту. Записав в классическую одно­битную ячейку памяти определен­ное значение, мы именно его оттуда и прочтем, если не произойдет ка­кой-нибудь ошибки.

Классической ячейкой может послужить и спин электрона. Од­нако квантовая механика позволя­ет записать в проекции спина боль­ше информации, чем в классике.

Для описания поведения кван­товых систем было введено понятие волновой функции. Существуют волновые функции, называемые собственными для какой-то кон­кретной измеряемой величины. В состоянии, описываемом собствен­ной функцией, значение этой вели­чины может быть точно предсказа­но до ее измерения. Именно с таки­ми состояниями работает обычная память. Квантовая же система может находиться и в состоянии с волно­вой функцией, равной линейной комбинации собственных функции, соответствующих каждому из воз­можных значений (назовем здесь такие состояния сложными). В сложном состоянии результат из­мерения величины не может быть предсказан заранее. Заранее из­вестно только, с какой вероятно­стью мы получим то или иное зна­чение. В отличие от обычного ком­пьютера, в квантовом для представ­ления данных используются такие ячейки памяти, которые могут на­ходиться в сложном состоянии. В нашем примере мы определили бы, что спин электрона с определенной вероятностью смотрит вверх и вниз, то есть можно сказать, что в кубит записаны сразу и 0, и 1. Количество информации, содержащееся в та­кой ячейке, и саму ячейку называют квантовым битом, или, сокращен­но, кубитом. Согласитесь, ячейки в сложных состояниях весьма не­обычны для классической теории информации. Каждому возможно­му значению величины, представ­ленной кубитом, соответствует ве­роятность, с которой это значение может быть получено при чтении. Эта вероятность равна квадрату мо­дуля коэффициента, с которым соб­ственная функция этого значения входит в линейную комбинацию. Именно вероятность и является ин­формацией, записанной в кубит.

Квантовую механику не случай­но называют иногда волновой ме­ханикой. Дело в том, что квантово-механические волновые функции ведут себя подобно световой или какой-либо другой волне. И для волновых функций, благодаря их способности интерферировать, также может быть введено понятие когерентности. Именно это свой­ство используется в когерентном квантовом компьютере. Набор кубитов представляется когерентны­ми волновыми функциями. Ока­зывается, что существует вполне определенный класс воздействий на квантовую систему, называе­мый унитарными преобразования­ми, при которых не теряется запи­санная в кубит информация и не нарушается когерентность волно­вых функций кубитов. Унитарные преобразования обратимы - по результату можно восстановить ис­ходные данные. После прохожде­ния через квантовый процессор, использующий унитарные преоб­разования, волновые функции ку­битов заставляют интерферировать друг с другом, наблюдая получаю­щуюся картину и судя по ней о результате вычисления.

Из-за того, что для представле­ния информации используются кубиты, в которых записано сразу оба значения - и 0 , и 1 , в процессе вычислений происходит парал­лельная обработка сразу всех воз­можных вариантов комбинаций би­тов в процессорном слове. Таким образом, в КК реализуется естест­венный параллелизм, недоступный классическим компьютерам. За счет возможности параллельной работы с большим числом вариантов, в идеале равным 2^N(где N - число кубитов), квантовому компьютеру необходимо гораздо меньше вре­мени для решения определенного класса задач. К ним относятся, на­пример, задача разложения числа на простые множители или поиск в большой базе данных. Для коге­рентного компьютера уже предло­жены алгоритмы, использующие его уникальные свойства. Кроме того, предполагается использовать КК для моделирования квантовых систем, что трудно или вообще невозможно сделать на обычных компьютерах из-за нехватки мощности или по принципиальным соображениям.

Все существующие на сегодняш­ний день обычные компьютеры, да­же с параллельной обработкой ин­формации на многих процессорах, могут быть смоделированы так на­зываемым клеточным автоматом Тьюринга. Это существенно детер­минированная и дискретная маши­на. С возникновением и обсуждени­ем идей квантовых вычислений ста­ла активно развиваться квантовая теория информации и, в частности, теория квантовых клеточных авто­матов - ККА. Квантовый клеточный автомат является обобщением авто­мата Тьюринга для КК. Сформули­рована гипотеза, гласящая, что каж­дая конечным образом реализуемая физическая система может быть дос­таточно хорошо смоделирована универсальной моделью квантовой вычислительной машины, исполь­зующей ограниченное количество ресурсов. Для одного из предложенных типов ККА теоретически уже доказано, что он подходит для тако­го моделирования и не противоре­чит квантовой теории.

Пытаясь осуществить свой за­мысел, ученые упираются в про­блему сохранения когерентности волновых функций кубитов, так как потеря когерентности хотя бы од­ним из кубитов разрушила бы ин­терференционную картину. В на­стоящее время основные усилия экспериментальных рабочих групп направлены на увеличение отно­шения времени сохранения коге­рентности ко времени, затрачивае­мому на одну операцию (это отно­шение определяет число операций, которые можно успеть провести над кубитами). Главной причиной по­тери когерентности является связь состояний, используемых для ку­битов, со степенями свободы, не участвующими в вычислениях. На­пример, при передаче энергии элек­трона в возбужденном атоме в по­ступательное движение всего ато­ма. Мешает и взаимодействие с ок­ружающей средой, например, с со­седними атомами материала ком­пьютера или магнитным полем Зем­ли, но это не такая важная проблема. Вообще, любое воздействие на ко­герентную квантовую систему, ко­торое принципиально позволяет получить информацию о каких-ли­бо кубитах системы, разрушает их когерентность. Потеря когерентно­сти может произойти и без обмена энергией с окружающей средой.

Воздействием, нарушающим когерентность, в частности, явля­ется и проверка когерентности. При коррекции ошибок возникает сво­его рода замкнутый круг: для того чтобы обнаружить потерю коге­рентности, нужно получить ин­формацию о кубитах, а это, в свою очередь, также нарушает когерент­ность. В качестве выхода предло­жено много специальных методов коррекции, представляющих так­же и большой теоретический инте­рес. Все они построе­ны на избыточном кодировании.

Если в области передачи инфор­мации уже созданы реально рабо­тающие системы и до коммерческих продуктов осталось лишь несколько шагов, то коммерческая реализация квантового когерентного процессо­ра - дело будущего. К настоящему времени КК научился вычислять сум­му 1+1! Это большое достижение, если учесть, что в виде результата он выдает именно 2, а не 3 и не 0. Кроме того, не следует забывать, что и пер­вые обычные компьютеры были не особенно мощны.

Сейчас ведется работа над дву­мя различными архитектурами процессоров: типа клеточного ав­томата и в виде сети логических элементов. Пока не известно о ка­ких-либо принципиальных пре­имуществах одной архитектуры перед другой. Как функциональ­ная основа для логических эле­ментов квантового процессора бо­лее или менее успешно использу­ется целый ряд физических явле­ний. Среди них - взаимодействие одиночных поляризованных фо­тонов или лазерного излучения с веществом или отдельными ато­мами, квантовые точки, ядерный магнитный резонанс и - наибо­лее многообещающий - объем­ный спиновый резонанс. Процессор, постро­енный на последнем принципе, в шутку называют «компьютером в чашке кофе» - из-за того, что в нем работают молекулы жидкости при комнатной температуре и ат­мосферном давлении. Кроме этих эффектов есть довольно хорошо развитая технология логических элементов и ячеек памяти на Джозефсоновских переходах, которую можно при соответствующих условиях приспособить под коге­рентный процессор.

Теорию, описывающую явле­ния, лежащие в основе первого типа логических ячеек, называют квантовой электродинамикой в по­лости или резонаторе. Кубиты хра­нятся в основных и возбужденных состояниях атомов, расположен­ных некоторым образом на равных расстояниях в оптическом резона­торе. Для каждого атома исполь­зуется отдельный лазер, приводя­щий его в определенное состояние с помощью короткого импульса. Взаимовлияние атомных состоя­ний происходит посредством об­мена фотонов в резонаторе. Ос­новными причинами разрушения когерентности здесь служат спон­танное излучение и выход фото­нов за пределы резонатора.

В элементах на основе ионов в линейных ловушках кубиты хра­нятся в виде внутренних состояний пойманных ионов. Для управле­ния логикой и для манипулирова­ния отдельными кубитами также используются лазеры. Унитарные преобразования осуществляются возбуждением коллективных кван­тованных движений ионов. Источ­никами некогерентности является спонтанный распад состояний ио­нов в другие внутренние состояния и релаксация в колебательные сте­пени свободы.

Сильно отличается от двух пре­дыдущих «компьютер в чашке ко­фе». Благодаря достоинствам данного метода этот ком­пьютер является наиболее реаль­ным претендентом на то, чтобы достигнуть разрядности 10 бит в бли­жайшее время. В компьютере на кол­лективном спиновом резонансе ра­ботают молекулы обычных жидко­стей (без всяких квантовых вывертов типа сверхтекучести). В качестве ку­битов используется ориентация ядерных спинов. Работа логических ячеек и запись кубитов осуществля­ется радиочастотными электромаг­нитными импульсами со специаль­но подобранными частотой и фор­мой. В принципе, прибор похож на обычные приборы ядерного маг­нитного резонанса (ЯМР) и исполь­зует аналогичную аппаратуру. Жиз­неспособность этого подхода обес­печивается, с одной стороны, очень слабой связью ядерных спинов с окружением и, потому, большим временем сохранения когерентно­сти (до тысяч секунд). Эта связь ос­лаблена из-за экранирования ядер­ных спинов спинами электронов из оболочек атомов. С другой стороны, можно получить сильный выход­ной сигнал, так как для вычислений параллельно используется большое количество молекул. «Не так уж сложно измерить спин четвертого ядра у какого-то типа молекул, если у вас имеется около числа Авогадро (10

---

²³ ) таких молекул», - говорит Ди Винченцо (Di Vincenzo), один из исследователей. Для определения результата непрерывно контроли­руют излучение всего ансамбля. Та­кое измерение не приводит к потере когерентности в компьютере, как было бы в случае использования толь­ко одной молекулы.

Ядерные спины в молекулах жидкости при комнатной темпера­туре хаотически разупорядочены, их направления равномерно рас­пределены от 0 до 4p. Проблема записи и считывания кажется не­преодолимой из-за этого хаоса. При воздействии магнитного поля спины начинают ориентироваться по полю. После снятия поля через небольшое время система снова приходит к термодинамическому равновесию, и в среднем лишь около миллионной доли всех спинов остается в состоянии с ориентацией по направлению поля. Однако бла­годаря тому, что среднее значение сигнала от хаотически направлен­ных спинов равно нулю, на этом фоне можно выделить довольно слабый сигнал от «правильных» спинов. Вот в этих-то молекулах с правильными ядерными спинами и размещают кубиты. Для коррек­ции ошибок при записи N кубитов используют 2N или больше спинов. Например, для N =1 выбираются такие жидкости, где какие-то два спина ядер в одной молекуле после опре­деленного воздействия полем мо­гут быть ориентированы только одинаково. Тогда по направлению второго спина при снятии резуль­тата обработки можно отсеять нуж­ные молекулы, никак не влияя на первый спин.

Как уже было сказано, обработ­ка битов осуществляется радиоим­пульсами. Основным логическим элементом является управляемый инвертор. Из-за спинового взаимодействия резонансная час­тота, при которой происходит оп­рокидывание одного спина, зави­сит от направления другого.

Что касается квантовой передачи данных, к настоящему времени экспериментально реализованы системы обмена секретной информацией по незащищенному от несанкционированного доступа каналу. Они основаны на фундаментальном постулате квантовой механики о невоз­можности измерения состояния без оказания влияния на него. Подслушивающий всегда изменяет состояние кубитов, кото­рые он подслушал, и это может быть зафиксировано связы­вающимися сторонами. Данная система защиты информации абсолютно надежна, так как способов обойти законы кванто­вой механики пока еще никто не выдумал.

Область применения

Основное применение квантовым вычислениям — это искусственный интеллект. ИИ основан на принципах обучения в процессе извлечения опыта, становится все

---

точнее по мере работы обратной связи, пока, наконец, не обзаводится «интеллектом», пусть и компьютерным. То есть самостоятельно обучается решению задач определенного типа. Эта обратная связь зависит от расчета вероятности для множества возможных исходов, и квантовые вычисления идеально подходят для такого рода операций. Искусственный интеллект, подкрепленный квантовыми компьютерами, перевернет каждую отрасль, от автомобилей до медицины, и говорят, что ИИ станет для двадцать первого века тем, чем электричество стало для двадцатого.

Другой пример — это точное моделирование молекулярных взаимодействий, поиск оптимальных конфигураций для химических реакций. Такая «квантовая химия» настолько сложная, что с помощью современных цифровых компьютеров можно проанализировать только простейшие молекулы. Химические реакции квантовые по своей природе, поскольку образуют весьма запутанные квантовые состояния суперпозиции. Но полностью разработанные квантовые компьютеры смогут без проблем рассчитывать даже такие сложные процессы.

Квантовая криптография. Создание новых надежных алгоритмов шифрования. Например, чтобы взломать алгоритм классическим компьютером, нужно перебрать все возможные варианты. Это требует огромного количества времени, что делает эту операцию дорогостоящей и не практичной. А квантовые компьютеры могут выполнять такое разложение гораздо быстрее и эффективнее.

Как ни странно, глубокое изучение физики с применением квантовых компьютеров может привести… к изучению новой физики. Модели физики элементарных частиц зачастую чрезвычайно сложные, требуют пространных решений и задействуют много вычислительного времени для численного моделирования. Они идеально подойдут для квантовых компьютеров, и ученые уже положили на них глаз. Ученые Университета Инсбрука и Института квантовой оптики и квантовой информации (IQOQI) недавно использовали программируемую квантовую систему для подобных манипуляций с моделями. Для этого они взяли простую версию квантового компьютера, в котором ионы производят логические операции, базовые шаги в любом компьютерном расчете. Моделирование показало прекрасное соглашение с реальными, описанными физикой, экспериментами.

И это не весь список, ведь по мере развития квантовых компьютеров будут расширяться возможности и сферы их применений.

Заключение

---

Вместе с квантовым компьютером наступит новая эра вычислений и научных открытий. Если создать квантовый компьютер из 200 кубитов, то мощность этого компьютера будет равна больше, чем число атомов во всей вселенной. Что позволит моделировать различные физические системы.

Пока квантовые компьютеры способны выполнять простые задачи. Но в дальнейшем, с развитием квантовых технологий и вычислений, они будут способны выполнять очень сложные задачи, которые не способен выполнить простой компьютер. В квантовом компьютере скрыт большой потенциал.

Не исключе­но, что в информационном обще­стве появление квантового компь­ютера сыграет ту же роль, что в свое время, в индустриальном, - изоб­ретение атомной бомбы. Действи­тельно, если последняя является средством «уничтожения мате­рии», то первый может стать сред­ством «уничтожения информа­ции» - ведь очень часто то, что известно всем, не нужно никому.

Литература

1. Манин Ю.И. Вычислимое и невычислимое. - М.: Советское ра­дио, 1980. – С. 17-101. – ил. (Кибернетика).

2. Feynman R.P. Simulating Physics with Computers. / R.P. Feynman // International Journal of Theoretical Physics. – 1982. – Vol. 21, №12. – P. 467-788.

3. Фейнман Р.Ф. Квантовомеханические ЭВМ. / Р.Ф. Фейнман; пер. с англ. Б. Ф. Полковникова под ред. И. И. Мазина. // Успехи физических наук. Т.149, Физика наших дней. – 1986. – №4. – С. 671–688.

4. Deutsch D. Quantum theory, the Church-Turing principle and the universal quantum computer. / D. Deutsch // Proceeding of the Royal Society of London. – 1985. – A400. – P. 97.

5. Deutsch D. Quantum computational networks / D. Deutsch // Proceeding of the Royal Society of London. – 1989. – A425. – P. 73.

6. Yao А.С. – С. Quantum circuit complexity. / А.С. Yao // Proceedings of the 34th Annual Symposium on the Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, CA. – 1993. – P. 352.

7. Shor P.W. Algorithms for Quantum Computation: Discrete log and Factoring. / P.W. Shor; edited by S. Goldwasser. // Proceedings of the 35th Annual Symposium on the Foundations of Computer Science, IEEE Computer Society Press. – Los Alamitos, CA, 1994. – P. 124.

8. Валиев К.А. Квантовые компьютеры и квантовые вычисления. / К.А. Валиев // Успехи физических наук. Т. 175, Обзоры актуальных проблем. – 2005. – №1. – С. 3-39.

9. Китаев A.Ю. Квантовые вычисления: алгоритмы и исправление ошибок. / A.Ю. Китаев // Успехи математических наук. Т. 52. – 1997. – №6. – С. 53-112.

10. Grover L. Afast quantum mechanical algorithm for database search. / L. Grover // Proceedings of the 28th Annual ACM Symposium on Theory of Computing. – 1996. – Р. 212-219.

---