Федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

им. В.И. Ульянова (Ленина)»

кафедра физики

ОТЧЕТ

по лабораторной работе № 1

«ИССЛЕДОВАНИЕ

ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ МЕТОДОМ МОДЕЛИРОВАНИЯ

В ПРОВОДЯЩЕЙ СРЕДЕ»

Выполнила: Завьялов Никита Сергеевич

Группа № 2311

Преподаватель: Овезов Максат Кемалович

Вопросы		Задачи ИДЗ					Даты коллоквиума		Итог

Санкт-Петербург, 2023

Лабораторная работа 1. Исследование
электростатического поля методом моделирования
в проводящей среде

ЦЕЛЬ РАБОТЫ: исследование конфигурации электростатического поля; построение эквипотенциалей и линий напряженности для заданной формы электродов; приобретение навыков в применении теоремы Гаусса на примере определения электроемкости системы по экспериментально найденному распределению поля.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: пантограф с зондом, измерительная схема, лист чистой бумаги.

ОСНОВНЫЕ СВЕДЕНИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ

Электростатическое поле определено, если в каждой точке пространства известны величина и направление вектора напряженности

---

E или значение потенциала  этого поля. В первом случае мы имеем дело с векторным представлением поля, во втором – со скалярным. Между этими представлениями существует связь, выражающаяся соотношением

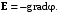(1.1)

В диэлектриках электростатическое поле характеризуется вектором электрического смещения (электрической индукции) 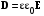, который удовлетворяет теореме Гаусса: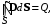



где Q – суммарный сторонний заряд, заключенный в объеме, ограниченном поверхностью S. Для однородного диэлектрика

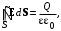(1.2)

Электрическое поле потенциально, т. е. работа электрических сил по перемещению заряда не зависит от формы траектории; работа по замкнутому пути равна нулю. Математически это соответствует тому, что циркуляция вектора напряженности электростатического поля также равна нулю:
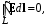(1.3)

Соотношения (1.2) и (1.3) дают исчерпывающее описание свойств электростатического поля. В данной работе рассматриваются две типичные задачи электростатики: определение  и E поля заданного распределения зарядов и вычисление емкости системы проводников.

Во многих случаях прямой расчет электростатического поля заменяют его моделированием. Наиболее удобной моделью является электрическое поле в проводящей среде.

Если электроды, к которым приложена разность потенциалов, помещены в проводящую среду, то в межэлектродном пространстве возникает электрический ток, плотность j которого связана с напряженностью E электрического поля, установившегося в среде, законом Ома:

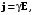(1.4)

где  – удельная проводимость среды.

Таким образом, линии тока (траектории носителей тока в проводящей среде) совпадают с линиями напряженности электрического поля. В отсутствие сторонних сил линии тока будут перпендикулярны поверхностям равного потенциала; следовательно, соотношение (1.1) справедливо и для электрического поля в проводящей среде.

Продолжая аналогию, можно для электрического поля в проводящей среде найти соотношение, подобное теореме Гаусса (1.2). Если не рассматривать перенос заряда сторонними силами, то из очевидного выражения

---

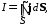
где I – ток, текущий от электрода, а S – замкнутая поверхность, охватывающая электрод, придем к соотношению



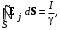
подобному (1.2). Потенциальный характер электрического поля в проводящей среде иллюстрируется соотношением



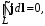
которое легко доказать, вычисляя, например, циркуляцию вектора j по замкнутому контуру L, расположенному на эквипотенциальной поверхности. Учитывая (1.4), получим подобное (1.3) выражение:



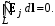
На основании подобия свойств векторов E и E_j можно сделать вывод о возможности моделирования электростатического поля электрическим полем в проводящей среде, если соблюдается подобие формы и расположения электродов в пространстве. Масштабные коэффициенты проводящей модели вычисляются из сопоставления тока I и заряда Q, а также удельной проводимости и абсолютной диэлектрической проницаемости модели и электростатического аналога с учетом их размеров.

Электрическое поле проводящей модели определяют, измеряя распределение потенциалов в ней, после чего, используя (1.1), рассчитывают поле вектора напряженности.

Электроемкость системы электродов определяют прямым измерением сопротивления проводящей среды между электродами. Можно показать, что



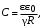
где R – сопротивление проводящей среды.

Можно также вычислить емкость электродов с использованием теоремы Гаусса, учитывая, что

C = Q/U,

где U – напряжение, равное разности потенциалов между электродами модели, получаем для определения емкости

(1.5)

где E_j – вектор, который вычисляется по поверхности, охватывающей электрод моделируемой системы;  – относительная диэлектрическая проницаемость моделируемого диэлектрика.

Соотношение (1.5) удобно тем, что в качестве поверхности S берется определенная по модели эквипотенциальная поверхность.

---

Смотрите также файлы

• Древнерусское государство и право.docx

• Определение менеджмента, его сущность, задачи, функции.docx

• Экзаменационный билет .doc

• Урок Тема жизни и смерти в рассказе В. Набокова Рождество Школа кгу Средняя школагимназия 9 города Актобе.docx

• Бізді айналамыздаы математика.docx