Файл: Методические указания и задания к расчетнографическим работам для студентов и курсантов специальности.doc

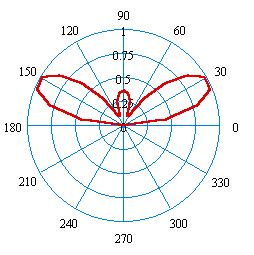
Рис. 4.5. Диаграмма направленности антенны в вертикальной плоскости

(при изменении угла ∆ через 7.5⁰)
Таблица 4.4
Варианты задания

Вариант	Исходн.	1	2	3	4	5	6	7
r, км	1000	500	600	800	1000	1500	2000	1500
Н, км	250	200	200	200	250	250	250	250
f, МГц	5	3	4	5	6	7	8	9

Вариант	8	9	10	11	12	13	14	15
r, км	1000	800	600	500	700	1000	1500	2000
Н, км	300	300	300	300	350	350	350	350
f, МГц	5	10	12	14	16	18	20	25

Вариант	16	17	18	19	20	21	22	23
r, км	500	600	800	1000	1500	2000	1500	1000
Н, км	300	350	350	350	350	250	250	300
f, МГц	5	7	9	5	6	7	8	10

---

5. Расчет основных характеристик волновода
Задание
Для волновода, имеющего поперечные размеры а и б, выполнить следующее:

1. Рассчитать критические частоты и критические длины волн для основной волны и первых пяти мод. Результат изобразить на графике.

2. Определить для первой моды длину волны в воздухе и в волноводе для частот, превышающих критическую частоту. Для расчета выбрать не менее 10 частот. Построить график зависимости длины волны в волноводе и длины волны в воздухе от частоты.

3. 
   Рассчитать для частот, указанных в п. 2, фазовую и групповую скорости волны в волноводе. Построить график зависимость фазовой и групповой скорости от частоты.
   
4. 
   Определить затухание волны в волноводе в дБ / м и построить график зависимости затухания от частоты (для того же частотного диапазона, что и в п.2).
   

Исходные данные
Поперечные размеры волновода:

а = 51 мм,

б = 25 мм.


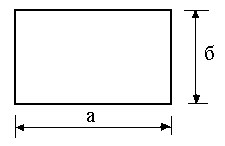
Рис. 5.1. Поперечные размеры волновода
Решение
1. В полом прямоугольном волноводе критическая частота связана с размерами волновода следующим образом:

, (5.1)

где: v – скорость распространения волны в среде, которой заполнен волновод (для воздуха v = c= 3^.10⁸ м / с); m и n– число полуволн, укладывающихся вдоль поперечных стенок волновода (определяемые типом волны); aи b – поперечные размеры внутренних стенок волновода.

Критическую длину волны можно определить из выражения:

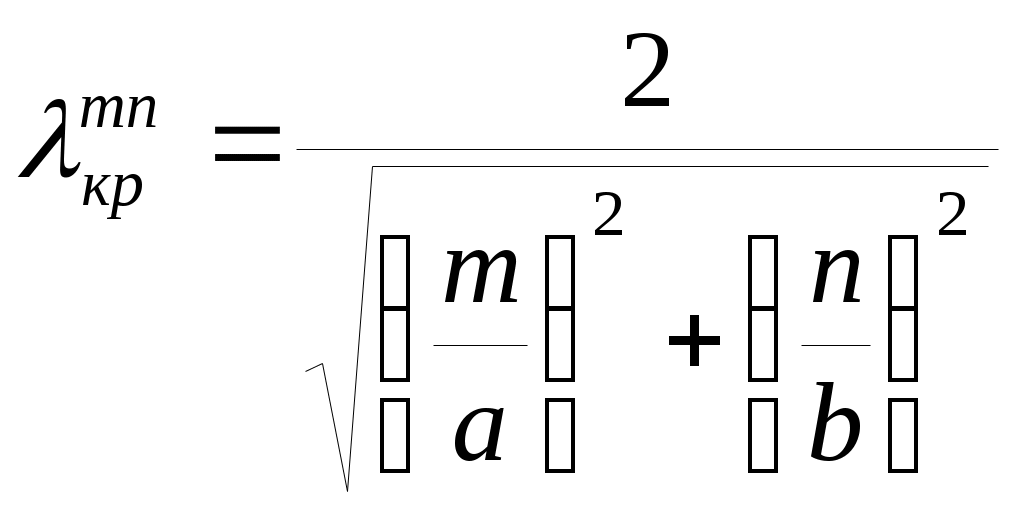. (5.2)

Если известна критическая частота, то критическую длину волны удобней вычислить по формуле:

λ_кр= v / f_кр, (5.3)

В полых металлических волноводах распространяются только Е- и H-волны. Класс волны определяется наличием или отсутствием продольных составляющих поля Е_z и Н_z, параллельных направлению распространения. Е-волны (электрические) имеют только одну продольную электрическую составляющую Е_z, а H-волны – только одну продольную магнитную составляющую Н_z. Тип волны, называемый также модой, определяется сложностью структуры поля волны данного класса. Он обозначается двумя числовыми индексами. Например, если мода Е

---

₁₃, то это означает, что это Е-волна и в поперечном сечении волновода параллельно одной стенки укладывается одна полуволна, параллельно другой – три полуволны.

Волну, обладающую в волноводе данной формы минимальной критической частотой, называют основной. Для H-волны основной является волна H ₁₀.

Определим критические частоты и критические длины волн для основной волны и первых пяти мод. Для этого выберем комбинацию чисел m и n. Основная волна имеет m= 1, n= 0. Поскольку мы не знаем, какие сочетания чисел m и n дадут первые 5 критических частот, поэтому зададимся с некоторым запасом значениями m и n. По формулам (5.1) и (5.3) вычислим значения критические частот и длин волн. Результат запишем в таблицу 5.1.
Таблица 5.1
Критические частоты и длины волн в волноводе

m	1	0	0	0	1	1	1	2	2	2	3	3	3
n	0	1	2	3	1	2	3	0	1	2	0	1	2
fкр, ГГц	2,94	6,0	12,0	18,0	6,68	12,3	18,2	5,88	8,4	13,4	8,82	10,7	14,9
Λкр, мм	102	50	25	16,7	44,9	24,3	16,5	51	35,7	22,5	34	28,1	20,1

Из таблицы 5.1 выберем основную волну и первые пять волн высших порядков. Данные занесем в таблицу 5.2 и построим график критических частот (рис.5.2).
Таблица 5.2
Критические частоты и длины волн в волноводе для основной волны и

---

первых пяти волн высших порядков.

m	1	2	0	2	3	3
n	0	0	1	1	0	1
fкр, ГГц	2,94	5,88	6,0	8,4	8,82	10,7
λкр, мм	102	51	50	35,7	34	28,1

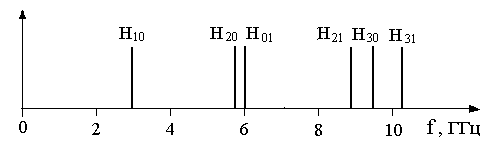
Рис. 5.2. Расположение критических частот Н-волны на частотной шкале
2. Определим для первой моды длину волны в волноводе по формуле:

, (5.4)

где длина волны в воздухе:

λ = c / f . (5.5)

Задаваясь значениями частоты f, вычислим длину волны в воздухе и в волноводе. Результаты расчета занесем в таблицу 5.3 и представим на графике рис. 5.3.
Таблица 5.3
Зависимость длины волны в воздухе и в волноводе от частоты

f, ГГц	2,94	3	3,2	3,4	3,6	3,8
λ, м	0,102	0,1	0,094	0,088	0,083	0,079
Λ, м	∞	0,503	0,237	0,176	0,144	0,125

f, ГГц	4	4,2	4,4	4,6	4,8	5,0
λ, м	0,075	0,071	0,068	0,065	0,063	0,06
Λ, м	0,111	0,1	0,092	0,085	0,079	0,074

---

3. Проведем расчет фазовой и групповой скорости волны в волноводе.

Фазовую скорость волны в волноводе определим из выражения:

(5.6)

где v – скорость волны в среде, которой заполнен волновод. В нашем случае v = с.

Рассчитаем групповую скорость волны в волноводе:

(5.7)




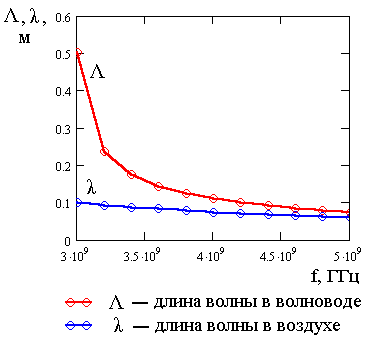
Рис. 5.3. Зависимость длины волны в волноводе и в воздухе от частоты
Задаваясь частотой f, рассчитаем зависимость фазовой и групповой скорости от частоты. Результат расчета занесем в таблицу 5.4 и представим в виде графика на рис. 5.4.
Таблица 5.4
Зависимость фазовой и групповой скорости в волноводе от частоты

f (ГГц)	2,94	3	3,2	3,4	3,6	3,8	4
v (м)	0,102	0,1	0,094	0,088	0,083	0,079	0,075
u (м)	∞	0,503	0,237	0,176	0,144	0,125	0,111

f (ГГц)	4,2	4,4	4,6	4,8	5,0
v (м)	0,071	0,068	0,065	0,063	0,06
u (м)	0,1	0,092	0,085	0,079	0,074

4. Вычислим затухание волны (в децибелах на метр) в волноводе:

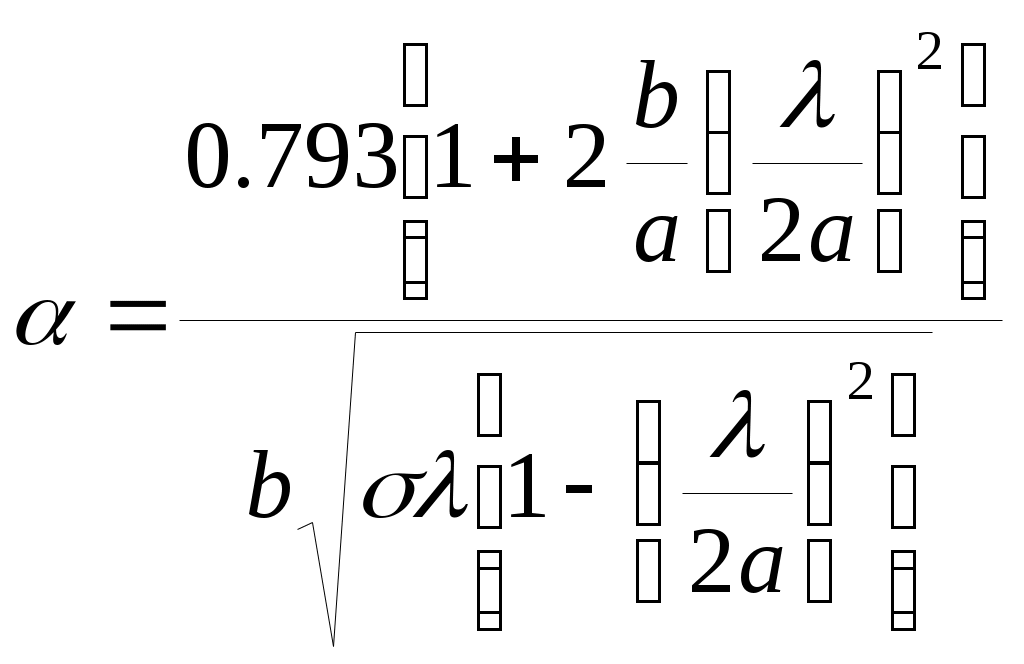, (5.8)

где а и b – внутренние размеры волновода, λ – длина волны в среде, σ – проводимость металла, из которого выполнены стенки волновода. Подставляя значения: а = 0,051 м, b = 0,025 мм, σ = 5,8

---