Файл: Решение Пронумеруем элементы цепи Введем основные события а цепь работает цепь отказала.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 26
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
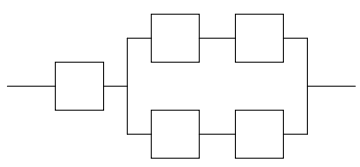
1. Электрическая цепь состоит из пяти элементов, выход из строя которых в заданный промежуток времени - независимые события, имеющие вероятности рi = 0,1 каждый. Найти вероятность P отказа цепи за данный промежуток времени.
Решение:
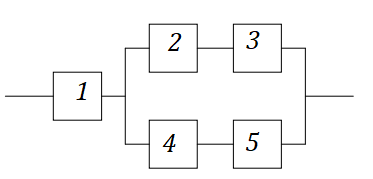
Пронумеруем элементы цепи:
Введем основные события:
А - цепь работает
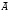 - цепь отказала
- цепь отказалаИзвестно, что Р(А)+Р(
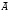 )=1
)=1Тогда Р(
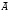 )=1-Р(А)
)=1-Р(А)Аi- элемент i работает и
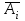 - элемент i отказал, i=1,2,...,n.
- элемент i отказал, i=1,2,...,n.Дано:
Р(
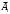 )=рi=0,1
)=рi=0,1Тогда Р(Аi)=qi=1-рi=0,9
Работаем с первым уровнем схемы. Нужно мысленно выделить крупные части, которые между собой соединены одинаково (параллельно или последовательно). В данном случае видно две группы элементов, соединенных последовательно (первая из элемента 1, вторая с элементами 2,3,4,5).
Если соединение последовательное, нужно перемножать события, то есть А=X1⋅X2
X1 - работает первая группа элементов,
X2 - работает вторая группа элементов,
Теперь смотрим на каждую группу. В первой группе всего один элемент, то есть она работает, когда работает ее элемент цепи (X1=А1). Мы дошли до элементов, разбор этой группы закончен.
Рассмотрим поближе вторую группу.
Видно, что вторая группа имеет уже параллельную структуру из элементов (они «висят» на параллельных линиях). Так как элементы соединены параллельно, речь идет о сумме этих событий, то есть вторая группа работает если:
X2=А2*А3+А4*А5
Сводим все в одну формулу и выпишем искомое событие (цепь работает безотказно):
А=X1⋅X2 =А1*(А2*А3+А4*А5)
Р(А)=Р(А1*(А2*А3+А4*А5))=
=Р(А1)*Р(А2*А3+А4*А5)=
=Р(А1)*(Р(А2*А3)+Р(А4*А5)- Р(А2*А3)*Р(А4*А5))=
= Р(А1)*(Р(А2)*Р(А3)+Р(А4)*Р(А5)- Р(А2)*Р(А3)*Р(А4)*Р(А5))=
=q1*(q2*q3+q4*q5-q2*р3*р4*q5)=
=0,9*(0,9*0,9+0,9*0,9-0,9*0,9*0,9*0,9)=0,86751
И тогда Р(
 )=1-Р(А)=1-0,86751=0,13249
)=1-Р(А)=1-0,86751=0,13249Ответ: 0,13249
2. Дискретная случайная величина задана законом распределения pi(xi). Найти величину a, построить график функции распределения данной случайной величины. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины.
| xi | 0 | 1 | 2 | 3 | 4 |
| pi | 0,3 | 0,1 | a | 0,1 | 0,2 |
Решение:
Значение а найдем из условия:
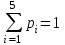
0,3+0,1+а+0,1+0,2=1
Тогда а=0,3
Ряд распределения примет вид:
| xi | 0 | 1 | 2 | 3 | 4 |
| pi | 0,3 | 0,1 | 0,3 | 0,1 | 0,2 |
Найдем функцию распределения F(x)=
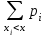
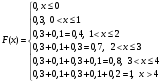
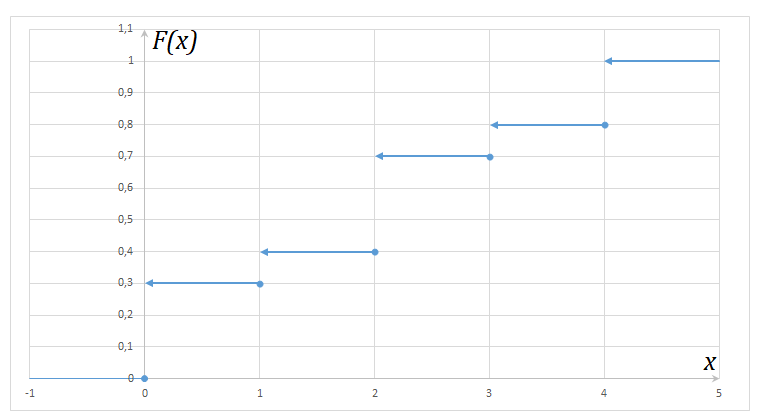
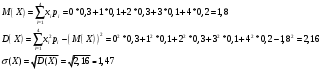
Ответ: а=0,3, М(Х)=1,8, D(X)=2,16, σ=1,47
3. Плотность распределения вероятностей непрерывной случайной величины задана выражением:
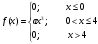
Найти величину коэффициента a, написать аналитическое выражением и простроить график функции распределения, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Найти вероятности попадания данной случайной величины в интервалы (0,2) и (2,8).
Решение:
Используя свойство нормированности
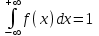 , найдем постоянную
, найдем постоянную
a
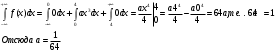
Найдем функцию распределения F(x), используя формулу
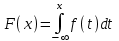
При
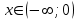 имеем:
имеем: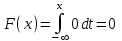
При
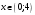 имеем:
имеем: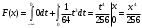
При
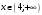 имеем:
имеем: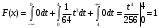
Таким образом,
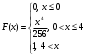
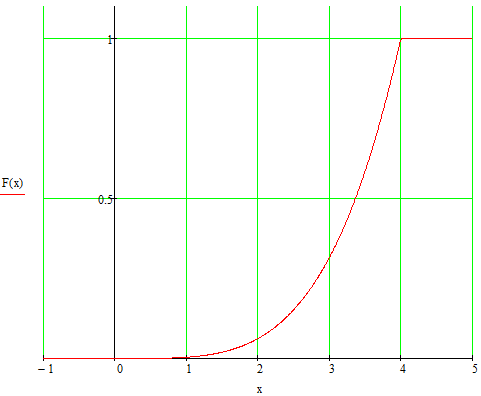
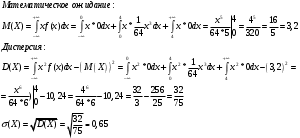
Вероятность попадания величины Х в интервал (0; 2):
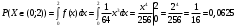
Вероятность попадания величины Х в интервал (2; 8):
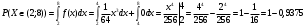
Ответ: а=1/64, М(Х)=3,2, D(X)=32/75, σ(X)=0,65,
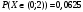 ,
, 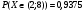
4. Дана нормально распределенная случайная величина с математическим ожиданием m=3 и дисперсией
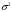 =2. Найти вероятность попадания данной случайной величины в интервал (2; 5).
=2. Найти вероятность попадания данной случайной величины в интервал (2; 5).Решение:
Используем формулу:
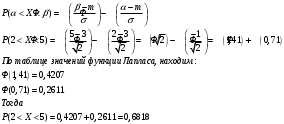
Примечание: Ф(x) — функция Лапласа, функция Лапласа нечетная, т.е. Ф(-x) = -Ф(x).
Ответ: 0,6818
5. Найти выборочный коэффициент корреляции для пары случайных величин:
| Y X | -2 | 0 | 2 |
| 0 | 10 | 30 | 20 |
| 1 | 20 | 0 | 20 |
Решение:
Найдем необходимые числовые характеристики.
Выборочные средние:
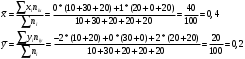
Дисперсии:
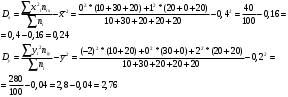
Откуда получаем среднеквадратические отклонения:
σx = 0.49 и σy = 1.66
и ковариация:
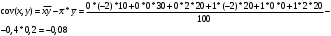
Определим коэффициент корреляции:
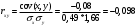
Ответ: -0,098