МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИОрдена Трудового Красного Знамени федеральное государственноебюджетное образовательное учреждение высшего образованияМосковский технический университет связи и информатикиКафедра многоканальных телекоммуникационных системЛабораторная работа № 3
по дисциплинеЦифровые системы передачи и методы их защитыРеализация принципов криптозащиты на основе средств микропроцессорной техникиБригада №7Выполнил:студент гр. БЗС2001Белов Д.БПроверил:ст.пр Мусатова О.ЮМосква 20231 Постановка задачи и исходные данные

1. 
   Средствами сигнального процессора ADSP-2181 реализовать базовую операцию умножения в простых полях Галуа в соответствии с индивидуальным заданием:
   

Zi=( Xi⋅Ki)mod p

2. 
   Средствами сигнального процессора ADSP-2181 реализовать базовую криптографическую операцию XOR в соответствии с индивидуальным заданием:
   

Yi=Xi⊕ KiИсходные данные:X_i={1614; 1316; 340; 33; 29}K_i={2239; 1316; 1614; 908; 12}P=22672 Краткая теорияМассивы и адресация ячеек в массивах Система команд сигнального процессора ADSP-2181 для выполнения операций с массивами, использует прямую и косвенную адресацию (смотрите с. 40-45 учебного пособия «Цифровые системы передачи и методы их защиты» [Электронный ресурс]. Режим доступа: https://lms.mtuci.ru/lms/local/mtt/elib_download.php?book_id=2375Организация циклов Смотрите с. 48 учебного пособия «Цифровые системы передачи и методы их защиты» [Электронный ресурс]. Режим доступа: https://lms.mtuci.ru/lms/local/mtt/elib_download.php?book_id=23753Разработанные блок-схемы программПрограмма умножения в простых полях Галуа

---

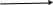
Подпрограмма деления из лабораторной работы №2

---

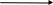
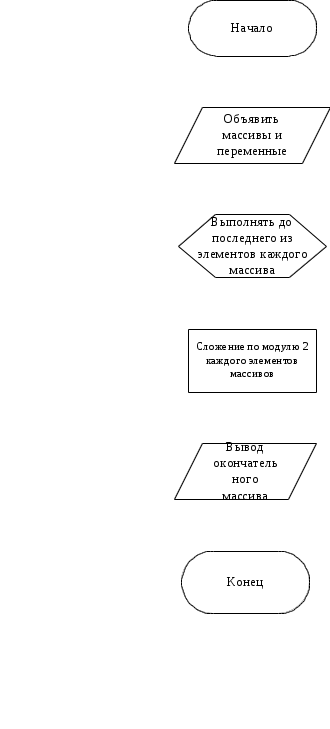
Программа реализации криптографической операции XOR4 Тексты программ.SECTION/DM vars;.var/circ X[5]=1614,1316,340,33,29;.var/circ K[5]=2239,1316,1614,908,12;.var/circ Z[5]=0,0,0,0,0;.var/circ Y[5]=0,0,0,0,0;.var p=2267;.SECTION/PM program;jump start; rti; rti; rti;rti; rti; rti; rti; rti; rti; rti; rti;rti; rti; rti; rti;rti; rti; rti; rti;rti; rti; rti; rti;rti; rti; rti; rti;rti; rti; rti; rti;rti; rti; rti; rti;rti; rti; rti; rti;rti; rti; rti; rti;start:I0 = X;L0 = length(X);I1 = K;L1 = length(K);I2 = Z;L2 = length(Z);I3=Y;L3=length(Y);M0=1;M1=-1;CNTR=5;do sumumn until CE;AX1=dm(I0,M0);AY1=dm(I1,M0);ar=AX1 XOR AY1;dm(I3,M0)=ar;MX1=AX1;MY1=AY1;ena m_mode;mr=MX1*MY1(uu);AX0=dm(p);call delen;sumumn: dm(I2,M1)=MR0; delen:AF=pass mr1;AY0=MR0;ASTAT=0;ar = pass ax0;if ne jump deli;astat = 4;rts;deli: ar = pass ax0;if gt jump deli_0;if lt jump deli_1;deli_1: sr1 = ax0;sr = lshift sr1 by -1(hi);divq sr1; divq sr1; divq sr1; divq sr1;divq sr1; divq sr1; divq sr1; divq sr1;divq sr1; divq sr1; divq sr1; divq sr1;divq sr1; divq sr1; divq sr1; divq sr1;ar = ay0;af = tstbit 0xf of ax0;if ne ar=ar-1;deli_0: divq AX0; divq AX0; divq AX0; divq AX0;divq AX0; divq AX0; divq AX0; divq AX0;divq AX0; divq AX0; divq AX0; divq AX0;divq AX0; divq AX0; divq AX0; divq AX0;divq AX0;mr2=0;my0=ax0;ar=pass ay0;mr=mr-ar*my0(uu);rts;5 Анализ полученных данныхПри выполнении программы в регистр AR был записан результат операции XOR. По умножению в простых полях Галуа в регистр AR было записано частное, в регистр MR0-остаток после операции mod p6 ВыводыМы научились производить операцию XOR и операцию умножения в простых полях Галуа с помощью сигнального процессора ADSP-2181

---

Смотрите также файлы

• московский международный университет Кафедра Юриспруденции.docx

• Московский финансовопромышленный университетСинергияКонтрольнокурсовое заданиеДата кодДисциплинаМаркетинг на основе данных.pdf

• Создание комфортных и оптимальных условий для деятельности пользователей внедрение современных компьютерных технологий в процесс исследования.docx

• Тест по экономике (Предмет, объект и методыэкономической теории)система подготовки к тестам Gee Test.pdf

• Алиментарные и алиментарнообусловленные заболевания.docx