Файл: Отчет по лабораторной работе по дисциплине Вероятностные модели инфокоммуникационных процессов Студента заочного отделения.doc

6. Сформировать ряд распределенный по экспоненциальному закону:

Математическое ожидание случайной величины, распределенной по показательному закону: Среднее квадратическое отклонение: Вероятность того, что случайная величина примет значение от 0,2 до 1   Ответ

(5)

7. Оценить математическое ожидание, оценить дисперсию случайной величины, имеющей экспоненциальный закон распределения, построить гистограмму.

В силу непрерывности функции распределения:
 – при этом и только при этом значении предложенная функция задаёт закон распределения  непрерывной случайной величины:


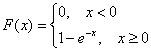
Пока, кстати, мы не знаем, что это за закон, ведь вверху я привёл другое определение.

2) Найдём функцию плотности распределения:

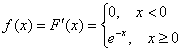
надеюсь, все в ладах с производной сложной функции:  .

Ну вот, теперь избушка повернулась к нам передом, а к лесу задом. Поскольку данная функция имеет вид  , то случайная величина   распределена показательно. Даже образцово-показательно, т.к. значение   наиболее приятно.

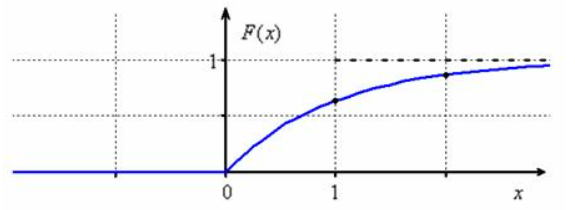
3) Условие допускает схематическое построение графиков, но зачем занижать планку? Даже при их ручном построении не составляет никакого труда найти пару дополнительных точек и проявить маломальскую аккуратность.

---

Вычислим пару значений   и простенький предел  . Таким образом, прямая   является горизонтальной асимптотой для графика   при 




Контрольные вопросы

1. Напишите аналитическое выражение плотности вероятности равномерного закона распределения.

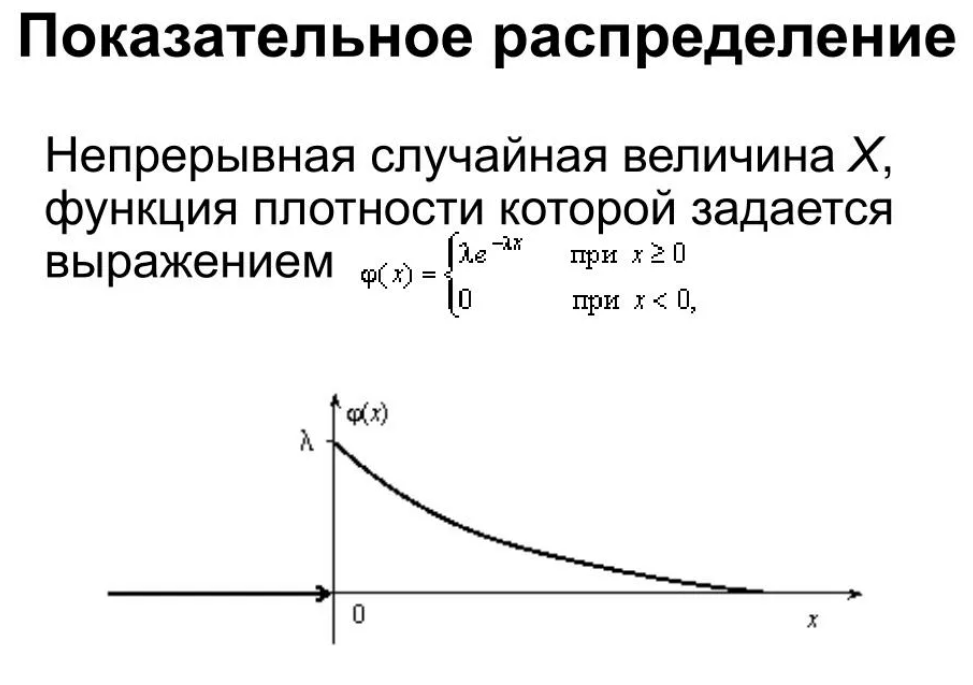
2. Напишите аналитическое выражение плотности вероятности экспоненциального закона распределения.

3. Напишите аналитическое выражение плотности вероятности нормального закона распределения.

4. Приведите график плотности вероятности равномерного закона распределения.

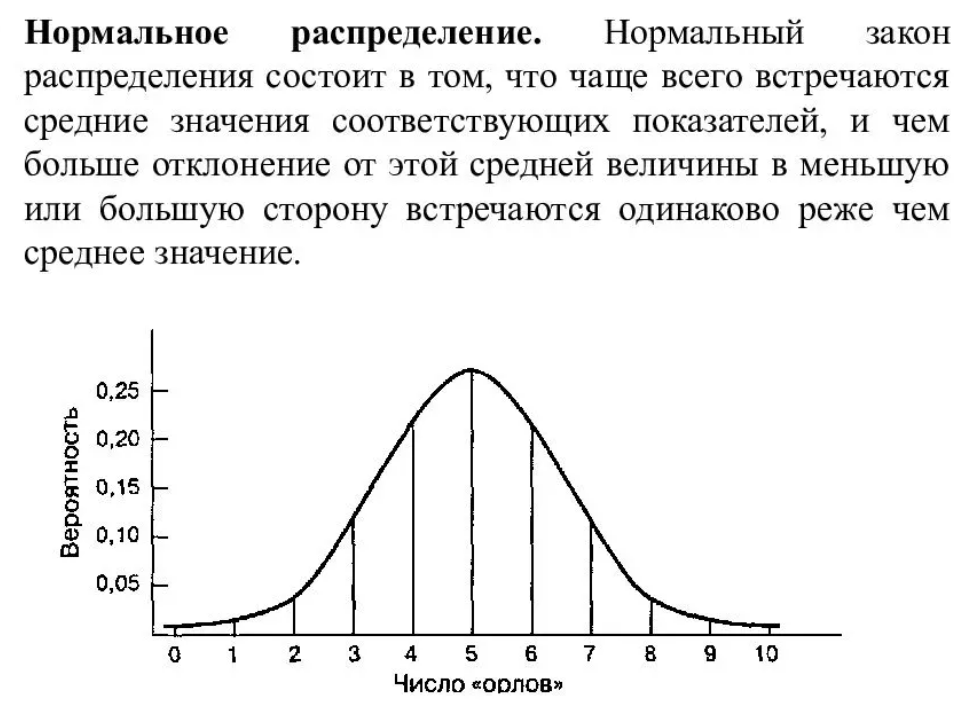
5. Приведите график плотности вероятности нормального закона распределения.

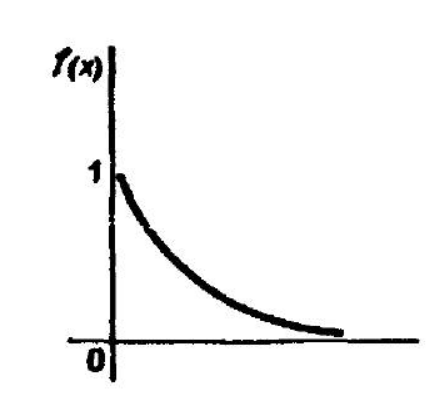
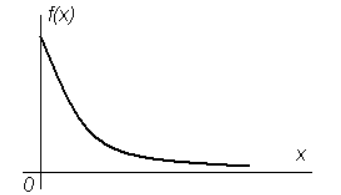
6. Приведите график плотности вероятности экспоненциального закона распределения.

7. Приведите формулу для построения последовательности на основе линейного конгруэнтного генератора.

8. Приведите формулу Бокса-Мюллера.

9. Приведите формулу для построения последовательности распределенной по нормальному закону.

1. Простейшее из непрерывных распределений, с помощью которого моделируются многие реальные процессы. И самый такой распространённый пример – это график движения общественного транспорта. Предположим, что некий автобус (троллейбус / трамвай) ходит с интервалом в 10 минут, и вы в случайный момент времени подошли к остановке. Какова вероятность того, что автобус подойдёт в течение 1 минуты? Очевидно, 1/10-я. А вероятность того, что придётся ждать 4-5 минут? Тоже  . А вероятность того, что автобус придётся ждать более 9 минут? Одна десятая!

2 .


3. Непрерывное распределение вероятностей. Это также называется распределением Гаусса. Функция плотности нормального распределения f (z) называется кривой Белла, потому что она имеет форму, напоминающую колокол.

---

4.

5.
6.
7. int i;

cin >> i;

srand(i); // установка начального значения

rand();

Функция srnd устанавливает начальное значение i.

8. Преобразование Бокса — Мюллера — метод моделирования стандартных нормально распределённых случайных величин. Имеет два варианта. Метод является точным, в отличие, например, от методов, основывающихся на центральной предельной теореме.
9.

---