Файл: Отчет по лабораторной работе по дисциплине Вероятностные модели инфокоммуникационных процессов Студента заочного отделения.doc

ФЕДЕРАЛЬНОЕ Государственное АВТОНОМНОЕ образовательное УЧРЕЖДЕНИЕ ВЫСШЕГО образования

БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ НАЦИОНАЛЬНЫЙ

ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ

(НИУ «БелГУ»)

ИНСТИТУТ ИНЖЕНЕРНЫХ И ЦИФРОВЫХ ТЕХНОЛОГИЙ
КАФЕДРА ИНФОРМАЦИОННО-ТЕЛЕКОММУНИКАЦИОННЫХ СИСТЕМ И ТЕХНОЛОГИЙ

Отчет по лабораторной работе по дисциплине: Вероятностные модели инфокоммуникационных процессов

Студента заочного отделения

2 курса 12002153 группы

Пасивенко А.Ю.
Проверил:

Асс. Ст. Пр. Голощапова В.А.


Белгород 2023

Лабораторная работа №2. Статистическая обработка результатов наблюдений

Цель работы: «Изучение основных понятий теории вероятности, ознакомление с основными характеристиками случайных величин и возможными способами их экспериментального определения».
1. Построение вариационного ряда.

Сформировать псевдослучайную последовательность (длиной 5000 значений), имеющую равномерный закон распределения. Последовательность постройте на основе линейного конгруэнтного генератора:

,

(1)

Листинг датчика на основе алгоритма сложения:

a = 565;

c = 323;

m = 56238423983;

x = ones;

n = 1000;

u = 1/m;

for i=1:n

x(i+1) = mod((a*x(i)+c),m);

u(i+1) = x(i+1)/m;

end

figure

histogram(u,n);
M = sum(u)/n;

disp("M = "); disp(M);

Dr = zeros;

for i=1:n

Dr(i) = (u(i)-M)^2;

end

D = sum(Dr)/n;

disp("D = "); disp(D);

Результат работы датчика сложения

Для построения гистограммы использовался массив N = 1000 при a = 565, c =323, m = 56238423983.



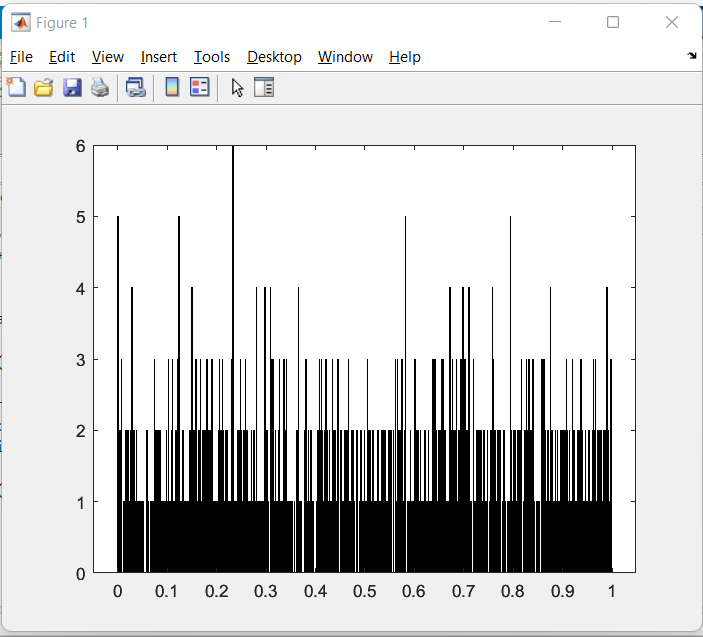
Рисунок 1 – Гистограмма, где размерность массива N равна 1000

---

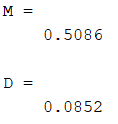
Таблица 1 – Варьируемые параметры для линейного конгруэнтного генератора

вариант параметры	1	2	3	4	5
- модуль	6075	6075	6655	7875	7875
- множитель	106	1366	936	211	421
- приращение	1283	1283	1399	1663	1663
- начальное заполнение	20	10	3	6	7

вариант параметры	6	7	8	9	10
- модуль	11979	11979	12960	14000	29282
- множитель	430	859	1741	1541	419
- приращение	2531	2531	2731	2957	6173
- начальное заполнение	5	345	23	265	32

вариант параметры	11	12	13	14	15
- модуль	29282	31104	53125	81000	86436
- множитель	1255	625	171	421	1093
- приращение	6173	6571	11213	17117	18257
- начальное заполнение	34	45	76	56	98

---

вариант параметры	16	17	18	19	20
- модуль	120050	121500	121500	121500	134456
- множитель	2311	1021	2041	4081	141
- приращение	25367	25673	25673	25673	28411
- начальное заполнение	12	35	67	12	32

вариант параметры	21	22	23	24	25
- модуль	134456	134456	139968	139968	145800
- множитель	281	8121	205	3877	3661
- приращение	28411	28411	29573	29573	30809
- начальное заполнение	23	45	76	24	34

2. Оценить математическое ожидание, оценить дисперсию равномерно распределенной случайной величины -

---

.

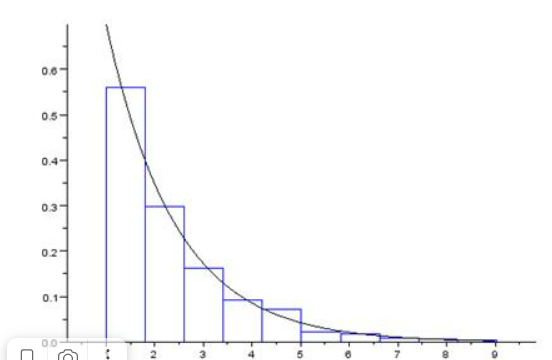
Плотность вероятности равномерного распределения на интервале: {2:8}



 

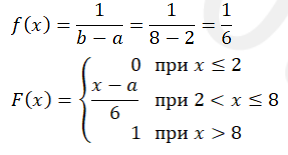
Искомая вероятность:



Ответ:
3. Построить гистограмму для нормированной к единице выборки .


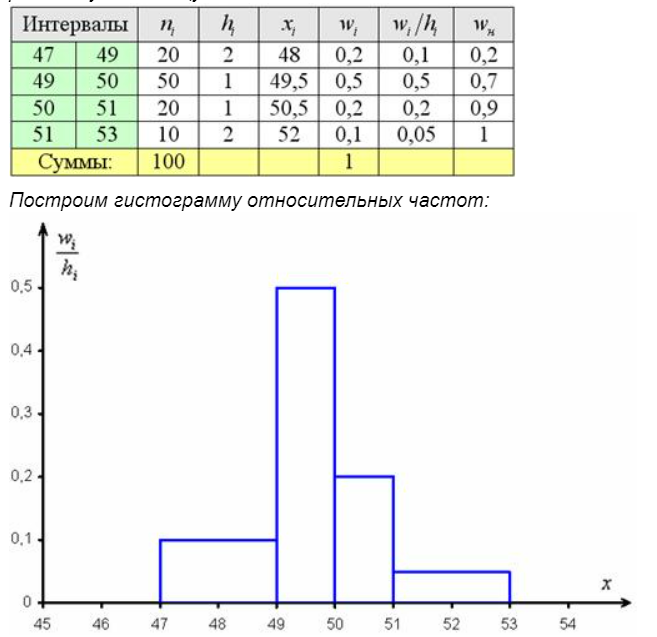
4. Сформировать ряд распределенный по нормальному закону:

,

(2)

,

(3)

,

(4)

или



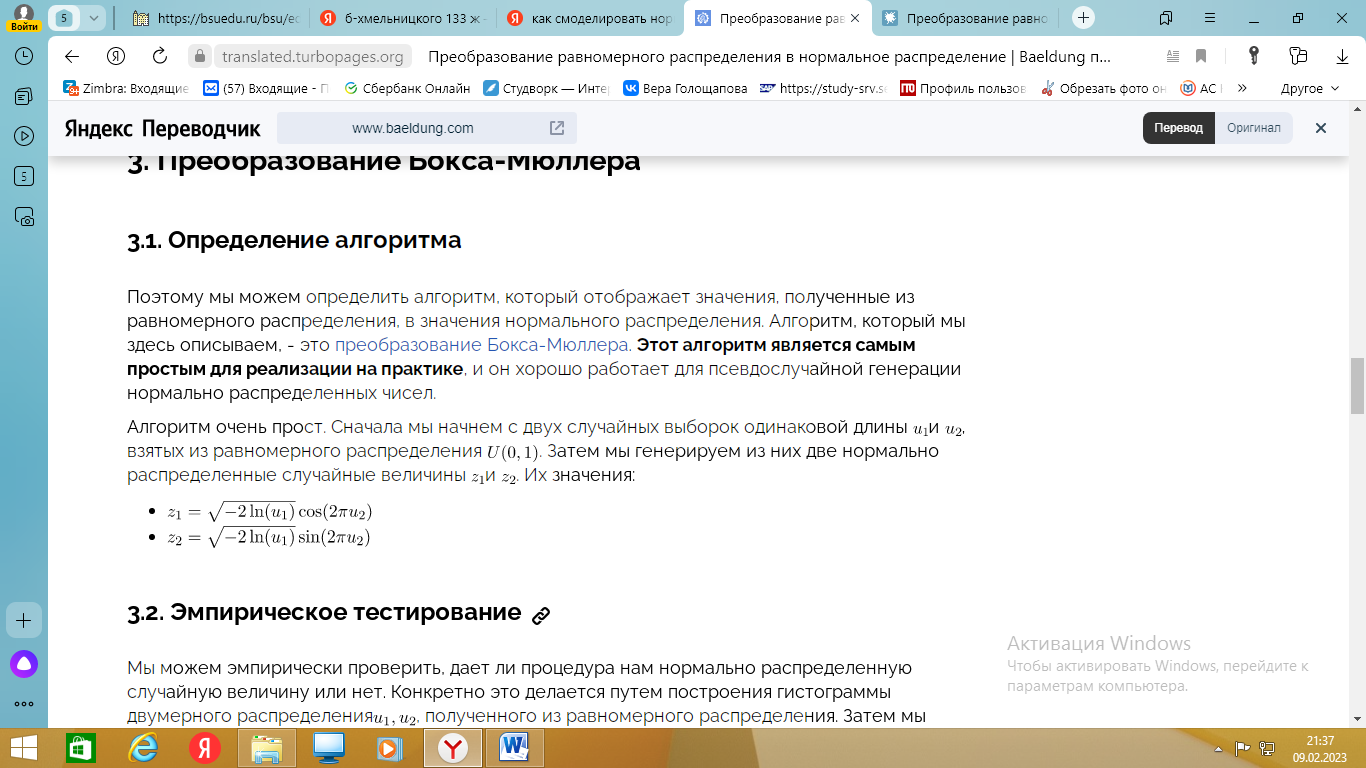
Вероятность того, что случайная величина, распределенная по нормальному закону, будет находиться в интервале : (A;B)



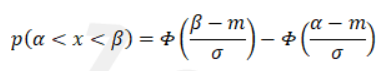
Получаем:
 

Вероятность того, что случайная величина, распределенная по нормальному закону, отклонится от среднего не более чем на величину :b.



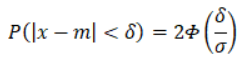
По условию

---

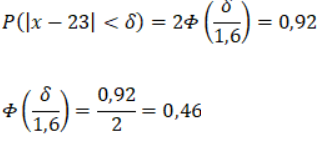
По таблице значений функции Лапласа:



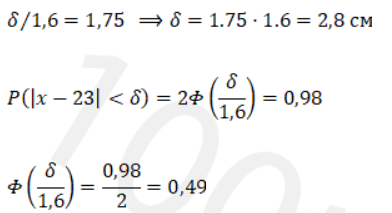
По таблице значений функции Лапласа:



 

По правилу трех сигм можно считать, что практически все длины деталей с вероятностью

0.9973 будут заключены в интервале

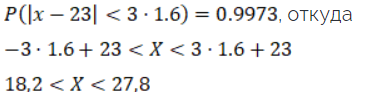
5. Оценить математическое ожидание, оценить дисперсию случайной величины с нормальным законом распределения, построить гистограмму.
Найдём функцию, обратную к функции распределения:



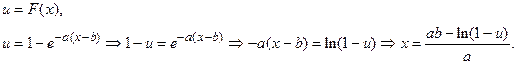
Таким образом, 

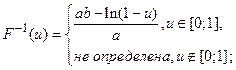
Теперь пусть у нас имеется случайная величина  . Тогда можно смоделировать случайную величину X как функцию от случайной величины U, обратную функции распределения случайной величины X:  . Пронаблюдав эту величину n раз, мы получим выборку объёма n.

Итак, у нас имеется выборка объёма n  , полученная при n наблюдениях за случайной величиной X. Требуется построить гистограмму распределения по этой выборке.

Аналогично расчетам из раздела 2.1.1 найдем выборочные максимум, минимум, количество интервалов группировки и ширину интервалов группировки. В нашем случае:  ,  , N = 10, 

---