ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 48
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Геометрические методы решения негеометрических задач
Исследовательская работа
Оглавление:
1. Введение…………………………………………………………………………………….3
2. Из истории развития геометрических методов………………………………………..4
3.Применение геометрических методов к решению задач………………………...5
3.1. Текстовые задачи………………………………………………………………….
3.2. Решение уравнений и систем уравнений………………………………………….
3.3. Решение тригонометрических задач………………………………………………
3.4. Решение взаимосвязанных иррациональностей………………………………….
3.5.Решение задач на вычисление наибольших и наименьших значений………….
4. Итог…………………………………………………………………………………………
5.Список литературы………………………………………………………………………….
Введение
Актуальность темы связана с необходимостью выработки навыка быстрого решения задач в условиях ограниченного времени при различных видах контроля знаний учащихся, например, тестирования, выполнения олимпиадных заданий, а так же с необходимостью поиска наиболее оптимальных способов решения различных задач.
Цель: изучить геометрический метод решения задач. Овладеть способами решения алгебраических задач геометрическими методами. Сравнить его с другими методами: арифметическим (по действиям) и алгебраическим (с помощью уравнений, неравенств и их систем). Выявить возможные преимущества.
Задачи:
1. используя различные источники, выделить алгебраические задачи, решаемые геометрическими методами;
2. провести сравнительный анализ различных методов решения задач;
3. рассмотреть способы решения задач геометрическими методами в тригонометрии;
4. рассмотреть решение геометрическими методами систем уравнений и уравнений;
5. провести исследование преимуществ данного метода.
6. провести анализ результатов;
7. создать компьютерную презентацию.
Объект исследования: Текстовые задачи, алгебраические задачи, тригонометрические задачи.
Предмет исследования: Геометрические методы решения
Гипотеза: геометрические методы решения задач являются более рациональными для выполнения большого числа заданий, и имеют важное значение для повышения математической культуры.
Работая над этой темой, я ставила перед собой цель: исследовать и изучить различные задачи, при решении которых используются геометрические методы.
Методы и приёмы исследования:
-
Изучение необходимого для решения задач теоретического материала. -
Проработка различных источников (учебники, различные математические журналы, ресурсы Интернет) и поиск наиболее интересных и сложных задач.
В работе можно найти имена ученых, которые применяли это понятие в своих научных работах и способствовали его развитию.
Изученные мною геометрические методы показывают, что довольно большое число примеров на решение уравнений, систем уравнений, стереометрических задач, задач на нахождение наибольших и наименьших значений существенно упрощается по сравнению с решениями, выполненными традиционным путем, а в некоторых случаях, особенно, когда много переменных, только такой подход и приводит к успеху. Думаем, что эта работа будет интересна ученикам, изучающим математику углублённо.
Из истории развития геометрических методов
Первые упоминания применения геометрических методов в алгебре известны еще со времен пифагорейцев, которые стали изображать величины с помощью отрезков и прямоугольников.
Сложение отрезков осуществлялось путем приставления одного из них к другому вдоль прямой, вычитание - путем отсечения от большего отрезка части, равной меньшему отрезку
Умножение осуществлялось путем построения прямоугольника на соответствующих отрезках.
Складывать можно было только однородные величины: отрезки с отрезками, прямоугольники с прямоугольниками. Во втором случае возникали трудности, ибо для объединения двух прямоугольников в один необходимо, чтобы у них была пара одинаковых сторон. Пифагорейцами для этого был разработан специальный прием (“Приложение площадей”), позволяющий данный прямоугольник преобразовать в равновеликий ему прямоугольник заданной высоты.
Дави́д Гильберт
Немецкий математик-универсал, внёс значительный вклад в развитие многих областей математики. В 1910—1920-е годы был признанным мировым лидером математиков. Гильберт разработал широкий спектр фундаментальных идей во многих областях математики, в том числе и аксиоматику евклидовой геометрии, а так же являлся автором много идей геометрических методов решения различных задач.
Арифметические знаки - это записанные геометрическиефигуры,
а геометрические фигуры – это нарисованные формулы.
Дьёрдь По́йа
Венгерский, швейцарский и американский математик, популяризатор науки.
Автор трудов по теории чисел, функциональному анализу, математической статистике и комбинаторике.
Обучение – это ремесло,
использующее бесконечное
количество маленьких трюков.
Применение геометрических методов к решению задач
При решении задач геометрическим методом нужно от алгебраической постановки задачи перейти к её геометрическому описанию. Затем, пользуясь свойствами фигур и взаимосвязями между ними, найти некоторые геометрические соотношения, отражающие данные и условия задачи, из которых можно получить решение задачи.
В ряде случаев при решении задач на вычисление, применение геометрических методов предпочтительнее традиционных конструктивных подходов. Чтобы успешно решать различные задачи с помощью геометрических методов, требуется не только знание свойств фигур, различных формул, но и определенная методика при составлении плана решения. Отметим несколько важных положений.
1. Рассмотреть задачу с точки зрения геометрической модели некоторых взаимосвязанных объектов.
2. Определить базовый уровень формул и теорем которые будут продвигать решение данной задачи.
3. Используя установленные взаимосвязи определить оптимальный ход решения и осуществить его.
Решение текстовых задач.
Алгебраизация математического образования, неправильное убеждение, что с помощью уравнений мы можем решить любую текстовую задачу, привели к почти полному исчезновению из школьного математического курса класса достаточно сложных, но от этого не менее красивых задач. Между тем существует целый ряд задач, в том
числе и встречающиеся на конкурсном экзамене, которые гораздо удобнее решать «геометрически», чем «алгебраически». Решение задач осуществляется при помощи чертежей. Построение этих чертежей дает возможность «увидеть» задачу – установить и исследовать связи, существующие между величинами, входящими в задачу, выбрать кратчайший путь решения.
Например, для решения текстовых задач на движение удобно использовать графики и с помощью различных свойств геометрических фигур определять длины необходимых отрезков.
Очень часто в текстовых задачах рассматриваемая величина является произведением двух других. Поэтому, в таких задачах целесообразно перейти к методу площадей, для наглядности представляя такое произведение в виде площади прямоугольника, параллелограмма, или треугольника.
Задача 1
Из пунктов А и В навстречу друг другу вышли одновременно два поезда. Каждый из них двигался сначала равноускоренно (начальные скорости поездов равны нулю, ускорения различны), а затем достигнув некоторой скорости, - равномерно. Отношение скоростей равномерного движения поездов равно
. В некоторый момент времени скорости поездов оказались равными, а один из них прошел к этому времени расстояние в 
раза больше, чем другой. В пункты В и А поезда прибыли одновременно. Какую часть пути прошел каждый из поездов к тому моменту, когда их скорости оказались равными?Решение:
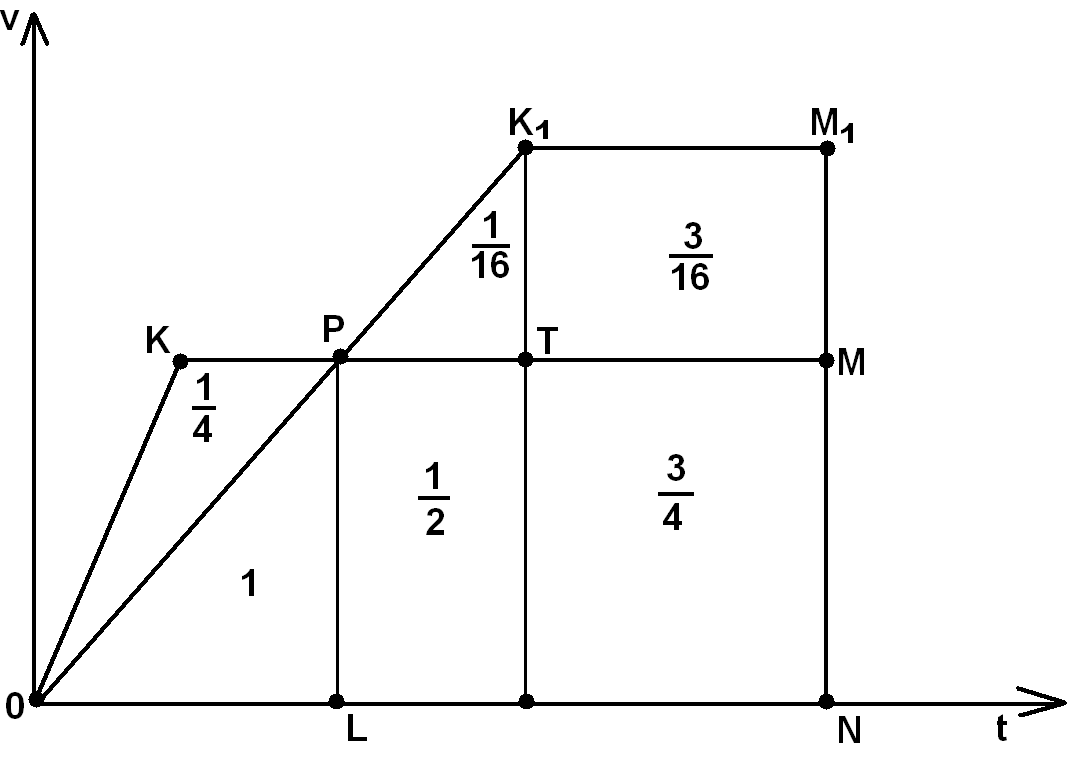
Рис. 10
Рассмотрим графики (рис. 10), изображающие зависимость скорости от времени, для каждого поезда. Для одного поезда графиком является ломанная ОКМ, для другого ОК1М1. длина пройденного пути равна площади соответствующей фигуры. По условию площади трапеций ОКМN и ОК1М1N равны; значит, равновелики и фигуры ОКР и РК1М1М. Площадь ОКРLравна
площади ОРL. Если площадь ОРL равна 1, то площадь ОКР есть
; площадь РК1Т равна 
. Поскольку К1Т=
. Затем легко определяем площади остальных частей.Ответ:
и 
.Решение уравнений и систем уравнений
Задача 2. Решите систему уравнений:
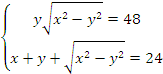
Решение:
Нетрудно убедиться, что x и y положительны.
Так как
, то числа y, 
и x являются длинами соответственно катетов и гипотенузы треугольника ABC с прямым углом ABC.Площадь этого треугольника 24 кв. ед., а его периметр 24 лин. ед. Тогда радиус окружности, вписанной в треугольник ABC, равен 2. Так как длина гипотенузы AB равна сумме длин катетов АС и ВС без удвоенной длины радиуса вписанной в этот треугольник окружности, то
.Из второго уравнения системы получаем x=10. Значит, y=6 или y=8.
Ответ: (10;6), (10;8).
Решение тригонометрических задач
Задача 3. Вычислите tg15
.Решение:
В
10 классе ученики, используя одну из теорем сложения, могут выполнить задание примерно так:
Но и в 9 классе эта задача не потребует много времени на её решение. Приведём его.
Рассмотрим равнобедренный треугольник АВС (АВ=ВС) с углов АВС, равным 30