ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 49
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Приведём в треугольнике высоты AD и BE. ∠CAD=15
. 
.
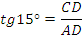Зная, что tg30˚=1/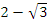
, очевидно, что
AD=1, AB=2 и BD=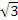
. Значит, CD= 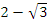. Вернемся к равнству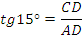
Ответ:
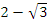
Решение взаимосвязанных иррациональностей
Задача 4. Решите уравнение.
.
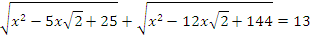Замечание. Иррациональные уравнения, согласно государственной программе по математике для средних общеобразовательных учреждений, решают в 11 классе. Стандартным приёмом ( возводить в квадрат обе части уравнения, до тех пор пока «не пропадут корни») эти уравнения решаются утомительно. Геометрические решения таких уравнений значительно короче.
Р
ешение.
Геометрическая интерпретация уравнения представлена на рисунке.
В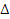
АВС по теореме Пифагора АВ=13.
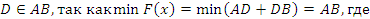
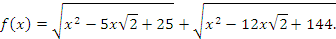
Заметим, что если уравнение имеет корни, то они должны быть положительными (при x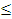
0 значение левой части уравнения не меньше 17).
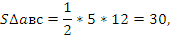
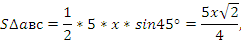
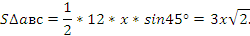
Значит,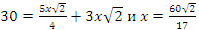
.
Ответ:
.
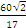Решение задач на вычисление наибольших и наименьших значений
Задача 5. Найдите наименьшее значение функции
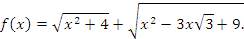
Решение.
Рассмотрим треугольник ACD (АC=2, CD=x, ∠ACD=90˚) и треугольник BCD (BC=3, CD=x, ∠BCD=30˚). Из треугольника ACD по теореме
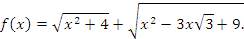
Пифагора АD=
А из треугольника ВСD по теореме косинусов:
.
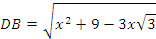
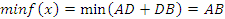Из треугольника ABC по теореме косинусов
.
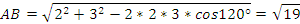Ответ: 
.
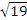Итог
Геометрические методы широко применяются при решении систем уравнений, тригонометрических задач, иррациональных уравнений и неравенств, вычисления наибольших и наименьших значений выражений и функций.
Решение большого числа задач существенно упрощается при применении геометрических методов по сравнению с решениями, выполненными традиционным путем, а в некоторых случаях, особенно, когда много переменных, только такой подход и приводит к успеху.
Хочется отметить что выдвинутая в начале работы гипотеза: «Геометрические методы решения задач являются более рациональными для выполнения большого числа заданий, и имеет важное значение для повышения математической культуры», подтвердилась.
Многие геометрические методы более лаконичны чем традиционные, изящны, интересны, необычны. Но они являются не менее эффективными.
Итогом моей заинтересованности стало, то, что я намного лучше стала понимать роль геометрических методов в математике, взаимосвязь курса алгебры и геометрии. Кроме того, геометрические методы позволяют «сжать» информацию, сделать ее наглядной и оперативной, и тем самым способствуют поиску путей решения математических заданий, что очень важно. И заметим, что приведенные выше решения задач не обладают для многих из нас признаком привычности, хотя они соответствуют школьной программе.
Надеюсь, что метод решения заданий, представленный мной, может оказать вам активную помощь при подготовке к итоговым и олимпиадным испытаниям. Также будет способствовать развитию и обогащению вашей математической культуры.
Список литературы
. . Зная, что tg30˚=1/
, очевидно, чтоAD=1, AB=2 и BD=
. Значит, CD= . Вернемся к равнству Ответ:
Решение взаимосвязанных иррациональностей
Задача 4. Решите уравнение.
.Замечание. Иррациональные уравнения, согласно государственной программе по математике для средних общеобразовательных учреждений, решают в 11 классе. Стандартным приёмом ( возводить в квадрат обе части уравнения, до тех пор пока «не пропадут корни») эти уравнения решаются утомительно. Геометрические решения таких уравнений значительно короче.
Р
ешение.Геометрическая интерпретация уравнения представлена на рисунке.
В
АВС по теореме Пифагора АВ=13. Заметим, что если уравнение имеет корни, то они должны быть положительными (при x
0 значение левой части уравнения не меньше 17).
Значит,
.Ответ:
. Решение задач на вычисление наибольших и наименьших значений
Задача 5. Найдите наименьшее значение функции
Решение.
Рассмотрим треугольник ACD (АC=2, CD=x, ∠ACD=90˚) и треугольник BCD (BC=3, CD=x, ∠BCD=30˚). Из треугольника ACD по теореме
Пифагора АD=
А из треугольника ВСD по теореме косинусов:
.Из треугольника ABC по теореме косинусов
.Ответ:
.Итог
Геометрические методы широко применяются при решении систем уравнений, тригонометрических задач, иррациональных уравнений и неравенств, вычисления наибольших и наименьших значений выражений и функций.
Решение большого числа задач существенно упрощается при применении геометрических методов по сравнению с решениями, выполненными традиционным путем, а в некоторых случаях, особенно, когда много переменных, только такой подход и приводит к успеху.
Хочется отметить что выдвинутая в начале работы гипотеза: «Геометрические методы решения задач являются более рациональными для выполнения большого числа заданий, и имеет важное значение для повышения математической культуры», подтвердилась.
Многие геометрические методы более лаконичны чем традиционные, изящны, интересны, необычны. Но они являются не менее эффективными.
Итогом моей заинтересованности стало, то, что я намного лучше стала понимать роль геометрических методов в математике, взаимосвязь курса алгебры и геометрии. Кроме того, геометрические методы позволяют «сжать» информацию, сделать ее наглядной и оперативной, и тем самым способствуют поиску путей решения математических заданий, что очень важно. И заметим, что приведенные выше решения задач не обладают для многих из нас признаком привычности, хотя они соответствуют школьной программе.
Надеюсь, что метод решения заданий, представленный мной, может оказать вам активную помощь при подготовке к итоговым и олимпиадным испытаниям. Также будет способствовать развитию и обогащению вашей математической культуры.
Список литературы
-
Колесникова С.И. Математика. Решение сложных задач единого государственного экзамена – 2-е изд., испр.- М.: Айрис-пресс, 2006. – 272с. – (Домашний репетитор: Подготовка к ЕГЭ) -
Математика. 9-11 классы: Решение заданий ЕГЭ высокой степени сложности. Основные методы и приемы/ Авт.-сост. М.А. Куканов. – Волгоград: Учитель, 2009. – 223с. -
Математика. Областные олимпиады. 8-11 классы/ [Н.Х. Агаханов, И.И.Богданов, П.А.Кожевников и др.] – М.: Просвещение, 2010 – 239с.: ил. – (Пять колец). -
Островский А.И., Кордемский Б.А. Геометрия помогает арифметике. М.:ФИЗМАТГИЗ, 1960. -
Энциклопедия для детей. [Том 11.] Математика. – 2-е изд., перераб. / ред. Коллегия: М. Аксёнова, В. Володин, М. Самсонов. – М.: Мир энциклопедий Аванта+, Астрель, 2007. – 621с. -
Якир М.С., Мерзляк А.Г., Полонский В.Б. Неожиданный шаг или сто тринадцать красивых задач. Киев: Агрорифма «Александрия». 1993. -
Библиотечка «Квант» -
Кушнир И. Геометрические решения негеометрических задач // №11. 1989. -
Ясиновый Э.Геометрия помогает решать уравнения // №12. 1984.