ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 437
Скачиваний: 36
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание №1. Фирма, работающая в условиях несовершенной конкуренции, максимизирует свою прибыль. Данныео работе фирмы представлены в таблице.Выпуск в ед. времени (Q), ед. 0 1
Цена, (P), руб. 140 115
Валовые издержки (TC), руб. 20 40
2 3 4 5
90 65 40 17
60 90 138 200
Определить:
1. При каком объеме выпуска и цене фирма максимизирует прибыль?
2. Чемубудут равны при этом объеме выпуска общий доход и общие издержки фирмы? Решение представить в табличной и графической форме.
Решение:
Условие максимизации прибыли при несовершенной конкуренции MR = MC.
Для определения оптимального объема производства, следует рассчитать валовой доход (TR = P*Q), прибыль (TP = TR – TC), предельные издержки (MC = ΔTC/ΔQ) и предельный доход (MR = ΔTR/ΔQ).Q P TC TR = P*Q
0 140 20 0
1 115 40 115
2 90 60 180
3 65 90 195
4 40 138 160
5 17 200 85
TP = TR-TC MC MR ATC
-20 - - -
75 20 115 40
120 20 65 30
105 30 5 30
22 48 -35 34,5
-115 62 -75 40
Как видно из таблицы, фирма достигает максимума прибыли при выпуске 2 единиц продукции по цене Р=90руб., в этом случае прибыль составит TP=120руб., общий доход будет равен TR=180руб., общие издержки TC=60руб., а предельный доход (MR=65) и предельные издержки (MC=20) принимают близкие значения.
Построим график.
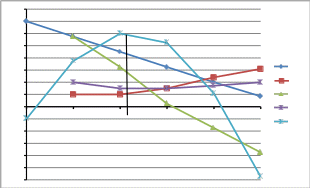160 140 120 10080
60 P 40 MC
20 MR
0 ATC -20 0 1 2 3 4 5 TP
-40
-60 -80 -100 -120
Задание №2. Город Сан Педро предлагает франшизы для открытия киосков на
улице по продаже драндулетов. Заинтересованные лица должны представить городу цену, по которой они будут продавать драндулеты. Заявки должны быть сделаны в запечатанных конвертах, и тот, кто представит самую низкую цену продажи, получит все франшизы. Если самая низкая цена будет представлена несколькими участниками, то они разделят рынок поровну. Спрос на драндулеты в Сан Педро представлен следующей функцией: Pd = 10 – 0,005Q, где Q – запрашиваемое количество драндулетов, Р – цена продажи.
P 10 9 8 7 6 5 4 3 2 1 0 Q 0 200 400 600 800 1000 1200 1400 1600 1800 2000
Предельные издержки
производства драндулетов постоянны и равны 1$ (постоянные издержки отсутствуют).
В настоящее время есть только два участника торгов. Ониоба хорошо знакомы друг с другом и согласны встретиться в ресторане «Вечерняя роза», чтобы обсудить возможное соглашение. Они решают назначить однуи ту же цену.
Таким образом, они поделят пополам франшизуи прибыль.
1. Если эти два участника объединятся в картель, какую цену они назначат на драндулеты?
2. Будет ли перспективным данное соглашение? Почему?
3. Если данное соглашение не будет перспективным, то какой
тогда будет равновесная цена на рынке, представленном двумя фирмам? Объясните.
Решение:
Для картеля в целом верно условие максимизации прибыли: MR=МС, т.е. предельный доход (MR) равен предельным издержкам (МС).
По условию задачи, спрос в отрасли определяется по формуле Pd=10–0,005Q, МС=1$. Предельный доход (MR) равен производной валового дохода (TR), т.е. MR=TR′.
В свою очередь TR=Р*Q. Найдем TR: TR=(10 ‒ 0,005Q)×Q=10Q ‒ 0,005Q2. Значит, MR=TR′= (10Q ‒ 0,005Q2)′=10 ‒ 0,01Q.
Тогда MR=10 – 0,01Q=1. Откуда 0,01Q=10 – 1,
0,01Q=9, Q = 900.
Так как фирмы делят рынок поровну, то qi=Q/2=900/2=450шт., а цена