Файл: Курсовой проект расчет и проектирование стропильной фермы Содержание Введение Исходные данные.rtf

Размещено на http://www.allbest.ru/

Техникум

Сварочное производство

Основы расчета и проектирования сварных конструкций


КУРСОВОЙ ПРОЕКТ

Расчет и проектирование стропильной фермы

Содержание
Введение

1. Исходные данные

1.1 Выбор типа фермы и материала покрытия

1.2 Определение высоты фермы и типа решетки

1.3 Определение узловых нагрузок

1.4 Определение опорных реакций

1.5 Определение усилий в стержнях фермы

1.6 Подбор сечений стержней фермы

1.7 Проектирование узлов фермы

Список используемой литературы

Введение
Фермой называется стержневая система, остающаяся геометрически неизменяемой после условной замены ее жестких узлов шарнирными. Фермы имеют назначение, по существу, такое же, как и балки сплошного сечения, но применяются для перекрытия значительных пролетов, когда проектирование сплошных балок (например, двутавровых) становится экономически невыгодным вследствие неполного использования материала стенки, напряжения в которой меньше, чем в полках (см. эпюру нормальных напряжений в поперечных сечениях балки на рис. 2.1), и необходимости

1. Исходные данные
Таблица 1

Пролет фермы	L	18	м
Длина панели	l	3	м
Толщина снегового покрова	H	0,5	м
Шаг колонн	B	12	м
Марка стали		14Г2

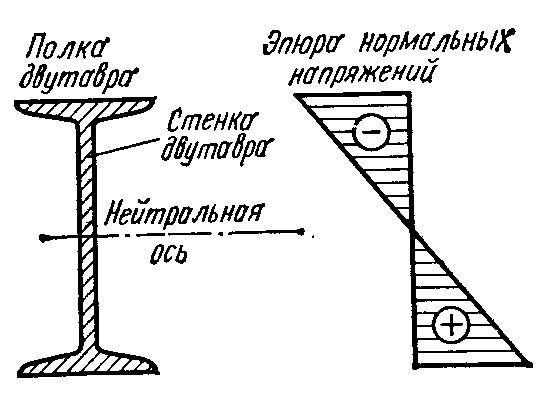
Рис. 1
утолщения вертикальной стенки в связи с возможностью ее выпучивания (при значительной высоте стенки). В таких случаях сплошную балку заменяют стержневой системой — фермой, элементы которой (стержни) при действии сосредоточенных нагрузок, приложенных в узлах, работают главным образом на центральное сжатие или растяжение. Это дает возможность значительно лучше использовать материал фермы, так как эпюры нормальных напряжений в поперечных сечениях каждого из ее стержней практически имеют вид прямоугольников. Поэтому ферма легче балки со сплошной стенкой, имеющей одинаковые с ней пролет и высоту. Примером фермы может служить система, изображенная на рис. 2.2.

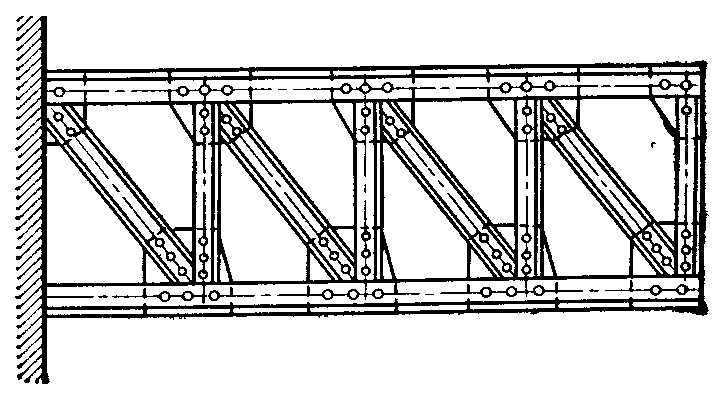
Рис. 2
Кроме плоских ферм, у которых оси всех стержней расположены в одной плоскости, применяются пространственные фермы, оси элементов которых не лежат в одной плоскости (рис. 2.3). Расчет пространственной фермы во многих случаях удается свести к расчету нескольких плоских ферм.


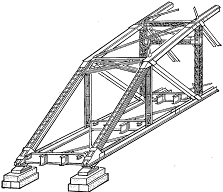
Рис. 3
поперечных сечениях каждого из ее стержней практически имеют вид прямоугольников. Поэтому ферма легче балки со сплошной стенкой, имеющей одинаковые с ней пролет и высоту. Примером фермы может служить система, изображенная на рис. 2.2.

Кроме плоских ферм, у которых оси всех стержней расположены в одной плоскости, применяются пространственные фермы, оси элементов которых не лежат в одной плоскости (рис. 2.3). Расчет пространственной фермы во многих случаях удается свести к расчету нескольких плоских ферм.

Расстояние между осями опор фермы (рис. 2.4, а) называется пролетом; стержни, расположенные по внешнему контуру фермы, называются пояснымии образуют пояса; стержни, соединяющие пояса, образуют решетку фермы и называются: вертикальные — стойками, наклонные — раскосами. Расстояние между соседними узлами любого пояса фермы (обычно измеряемое по горизонтали) называется панелью.


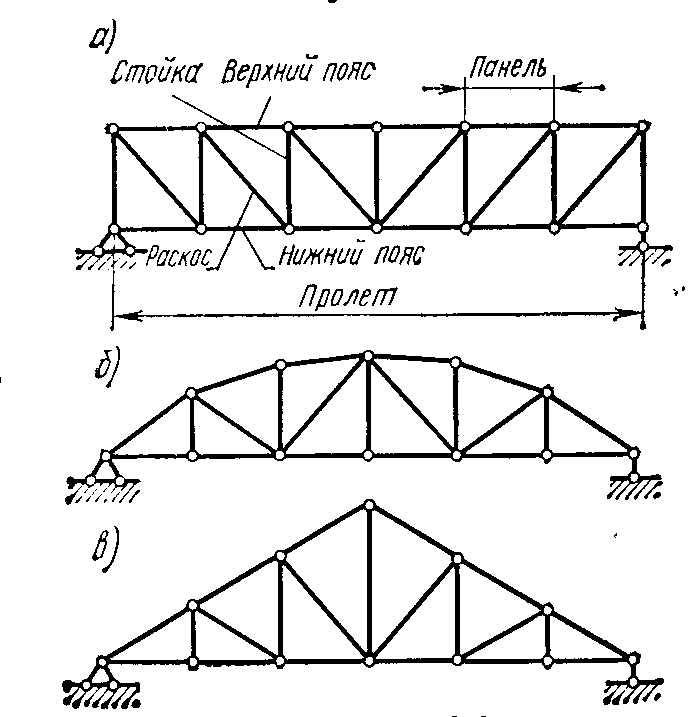
Рис. 4
Фермы классифицируют по следующим пяти признакам:

1) характеру очертания внешнего контура;

2) типу решетки;

3) типу опирания фермы;

4) назначению фермы;

5) уровню езды

По характеру очертания различают фермы с параллельными поясами (рис. 2.4, а) и с ломаным или так называемым полигональным расположением поясов. К последним относятся, например, фермы с параболическим очертанием верхнего пояса (рис. 2.4, б) и фермы треугольного очертания (рис. 2.4, в).


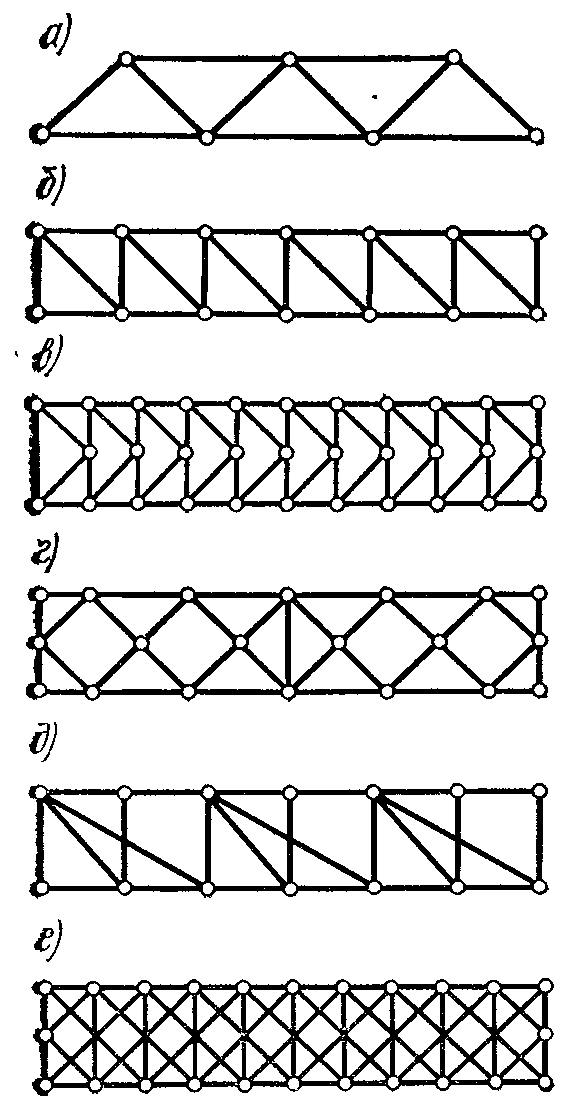
Рис. 5


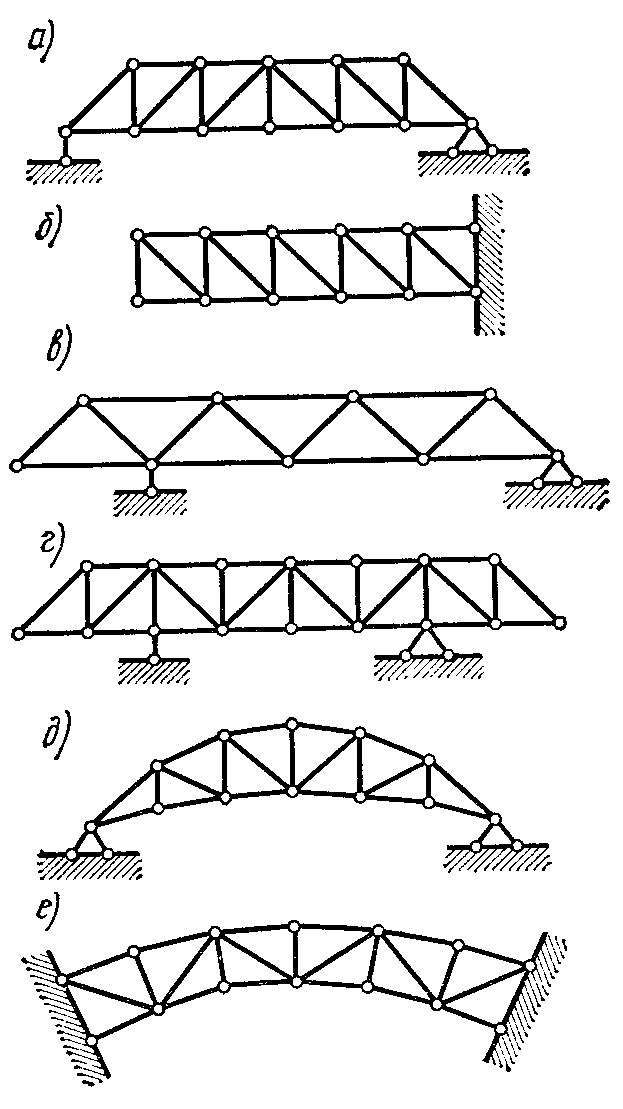
Рис. 6
По типу решетки фермы делятся на: фермы с треугольной решеткой (рис. 2.5, а); фермы с раскосной решеткой (рис. 2.5, б); фермы с полураскосной решеткой (рис. 2.5, б); фермы с ромбической решеткой (рис. 2.5, г); двухрешетчатые (рис. 2.5, д), многорешетчатые (рис. 2.5, е).

По типу о п и р а н и я фермы могут быть: закрепленными, у обоих концов — балочными (рис. 2.6, а) или арочными (рис. 2.6, д, е); консольными — закрепленными у одного конца (рис. 2.6, б); балочно-консольными (рис. 2.6, в, г).

В зависимости от назначения различают фермы стропильные (рис. 2.7, а), крановые (рис. 2.7, б), башенные (рис. 2.7, в), мостовые (рис. 2.8) и др.

Мостовые фермы в зависимости от уровня езды делятся на фермы с ездой понизу (рис. 2.8, о), фермы с ездой поверху, (рис. 2.8, б) и фермы с ездой посередине (рис. 2.8, в).


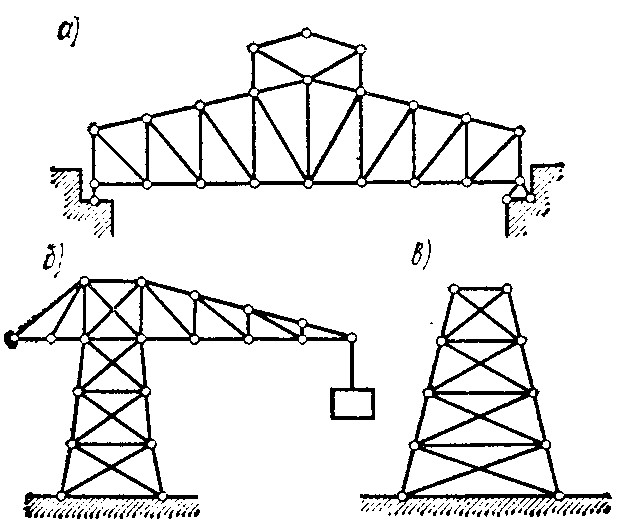
Рис. 7


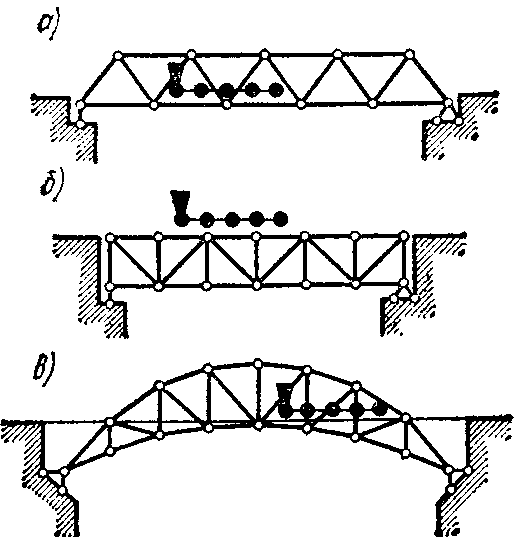
Рис. 8
1.1 Выбор типа фермы и материала покрытия
Выбор типа стропильной фермы определяется уклоном кровли:

- рулонные материалы по железобетонным плитам

i=1/8 ÷ 1/12 (α=7÷ 5о);
- кровельное железо
i=1/4 ÷ 1/5 (α=14 ÷ 11о);
- асбоцементные волнистые листы
i=1/4 ÷ 1/7 (α=15÷ 8о);
г) черепица α>30о.

Выбираем рулонные материалы по железобетонным плитам, которые образуют жесткий диск после монтажа, i=1/8 ÷ 1/12 (α=7÷ 5о). По ширине панели и шагу колонн выбираем плиту марки ПНКЛ-4 из условия передачи нагрузок на узлы.

По материалам покрытия принимаем двускатную (верхний пояс расположен под углом к нижнему) полигональную ферму.
1.2 Определение высоты фермы и типа решетки
Принимаем раскосную схему решетки с нисходящими опорными раскосами и опорными стойками. Направление раскосов выберем так, что бы все раскосы работали на растяжение, соответственно уменьшилось количество сжатых стержней сходящихся в узле, что упростит их проектирование и изготовление.

По ширине панели l=3м и оптимальному углу наклона раскоса α=450±100 принимаем высоту опорного раскоса hоп=3м.

Возвышение верхнего пояса

Δh=L/(2*i)=18 L/(2*12)=0,75м.
Тогда высота ферме в коньке
hк=hоп+ Δh=3+0,75=3,75м.
Условие соответствия железнодорожным габаритам hк˂3,85 м выполнено.

Опоры принимаем скользящие, для принятия с татически определимой расчетной схемы.


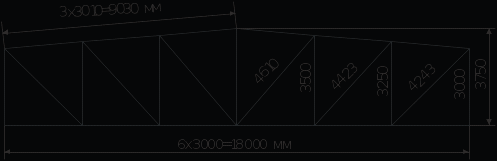
Рис. 9 Схема стропильной фермы.
1.3 Определение узловых нагрузок
Принимаем границы грузовой площади на один узел равными размеру железобетонной плиты, т.к. мы выбрали плиту с шириной равной l=3м и длиной L=12м. Тогда, =3х12=36 м2.

На крайние узлы ферм нагрузка будет равна половине промежуточной.

Постоянные нагрузки на ферму представлены в таблице 4.1
Таблица 2

Нагрузка	qнорм кг/м2	n	qрасч кг/м2
плита ПНКЛ-4 3х12м	189	11	208
металлоконструкции покрытия (ориентировочно)	30	1,1	33
асфальтовая стяжка	36	1,2	43
пенобетонная теплоизоляция Н=8см	48	1,2	58
трехслойного гидроизолирующего ковра	10	1,1	11
Всего:			353

В соответствии с приложением Г.1. СП 20.13330.2011 «СНиП 2.01.07-85 Нагрузки и воздействия» при уклонах двускатных покрытий α 20° принимаем вариант 1 по рис Г.1. и коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие =1, т.к. для покрытий из Ж/Б плит α=7÷ 5о


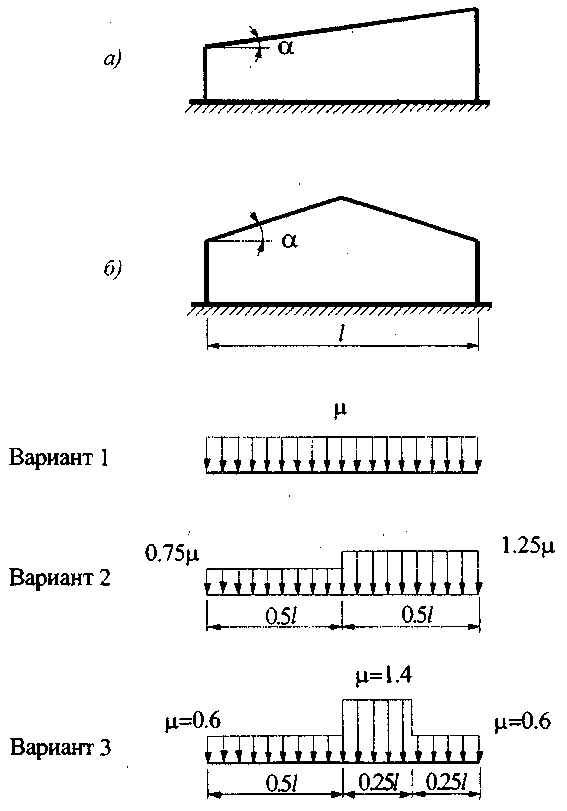
Рис Г. 10
Интенсивность снеговой нагрузки
qс=Н*1000Н/м3=0,5м*100кгс/м3=50кгс/м2
Тогда постоянные узловые нагрузи:
Nп=qрасч*Aгр =335*36=12060 кгс
Временные узловые нагрузки:
Nв=qс*Aгр+2P =50*36+2*100=2000кгс

Где 2P=200кгс-вес двух человек с инструментом.

Нагрузка на узлы фермы равна сумме постоянной и временной нагрузок:
N1расч=Nп +Nв=12060+2000=14060 кгс=14,06 тс=140,6кН
Нагрузка на крайних узлах фермы:
N2расч= N1/2=14060\2=7030кгс=7,03 тс=70,3кН
1.4 Определение опорных реакций
Опоры принимаем скользящие, для принятия статически определимой расчетной схемы.

В инженерной практике опорные реакции фермы определяются аналитически.

В случае симметричной нагрузки на ферму реакции опор будут равны.
FA = FB= ∑N/2 = (5N1+2N2)/2=42180кгс=42,180 тс=421,8кН
1.5 Определение усилий в стержнях фермы
Усилия в стержнях фермы найдем графическим методом По диаграмме Максвелла - Кремоны. Схемы стропильной фермы и распределения нагрузок приведены на рис. 5,1.
Таблица 3 Усилия в элементах фермы

Элемент	№ элемента	Усилие
		мм	тс
стойки	1-10 8-21	126,54	-42,180
	11-12 19-20	97,3375	-32,440
	13-14 17-18	51,2186	-17,071
	15-16	16,8720	-5,643
раскосы	10-11 20-21	137,6574	45,881
	12-13 18-19	69,7090	23,234
	14-15 16-17	10,1109	3,703
пояс верхний	2-11 7-20	97,6759	-32,555
	3-13 6-18	145,1184	-48,368
	4-15 5-16	152,3752	-50,787
пояс нижний	10-9 21-9	0	0
	12-9 19-9	97,3385	32,442
	14-9 17-9	144,6171	48,200
Масштаб сил; 1мм-0,3333 тс

1.6 Подбор сечений стержней фермы
Стержни фермы примем из парных равнополочных уголков. По максимальному усилию в элементах фермы N=50 тс определим конструктивную толщину косынок S=12 мм.

Раскосы. Сечение растянутых элементов 14-15 и 16-17 (наименьшее растягивающее усилие) определим по формуле:
=3,703*104 / 310=120 мм2=1,2см2,
площадь одного уголка
А=Атр/2= 1,2/2=0,6 см2
По сортаменту подбираем уголок №2 с толщиной полки 4 мм.

Определим радиусы инерции данного сечения:

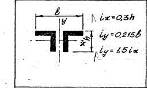
ix=0,3*h=0,3*2=0,6 см

iy=0,215*b=0,215*(1,2+2*2)=1,1 см

iy0=1,5* ix =1,5*0,6=0,9 см
Считая закрепления стержней шарнирными, что допустимо для плоских ферм примем приведенные длины стержней
lпр.14-15=l14-15 =461см длине стержня.
Найдем максимальную гибкость стержня:
=461/0,6=768, условие λ ≤ λпр не выполнено.

Предельная гибкость для растянутых элементов не должна превышать 400.

Необходимо увеличить площадь сечения. Принимаем профиль №4,5 с толщиной полки 3 мм, А=2,65см2.
ix=0,3*h=0,3*4,5=1,35 см

=461/1,35=341, условие λ ≤ λпр выполнено.
Найдем напряжение в стержне
σ=N / A)= 3,703*104 / 2*265=70 МПа
Недонапряжение составляет:
Δ σ=( R - σ)/ R =[(310-70) / 310]•* 100%=77% ˃5%
Сечение растянутых элементов 12-13 и 18-19 определим по формуле:
=23,234*104 / 310=749 мм2=7,5см2 , площадь одного уголка

А=Атр/2= 7,5/2=3,75 см2
По сортаменту подбираем уголок №5,6 с толщиной полки 3,5 мм, А=3,89см2

Определим радиусы инерции данного сечения:
ix=0,3*h=0,3*5,6=1,68см

=442,3/1,68=263, условие λ ≤ λпр выполнено.

Найдем напряжение в стержне
σ=N / A= 23,234*104 / 2*389=299 МПа
Недонапряжение составляет:
Δ σ=( R - σ)/ R =[(310-299) / 310]•* 100%=3,9% ˃5%
Что находится в пределах допустимого.

Сечение растянутых элементов 10-11 и 20-21 определим по формуле:
=45,881*104 / 310=480 мм2=14,8см2,
тогда площадь одного уголка
А=Атр/2= 14,8/2=7,4 см2
По сортаменту подбираем уголок №7,5 с толщиной полки 5 мм, А=7,39см2

Определим радиусы инерции данного сечения:
ix=0,3*h=0,3*7,5=2,25см

=424,3/2,25=189,
условие λ ≤ λпр выполнено.

Найдем напряжение в стержне

σ=N / A= 45,881*104 / 2*739=310 МПа
Недонапряжение составляет:
Δ σ=( R - σ)/ R =[(310-310) / 310]•* 100%=0% ˃5%
Что находится в пределах допустимого.

Верхний пояс. Подбор сечений наиболее нагруженных сжатых элементов 4-15 и 5-15 произведем по формуле:
= 50,783*104 / 310*0,460 = 3480мм = 34,8см2
где φ = 460 коэффициент продольного изгиба найдем по таблице приняв λпр =100 и Ry=310 МПа, т.к. предельная гибкость для сжатых элементов поясов и опорных стоек не должна превышать λпр=120.
Тогда =Атр / 2= 34,8 / 2=17,4 см2
По сортаменту подбираем профиль №11 с толщиной полки 7 мм. А=15,2см2 стропильный ферма покрытие стержень

Проверим гибкость стержня:
ix=0,3*h=0,3*11=3,3 см

=301/3,3=91
Условие λ ≤ λпр выполнено

Найдем напряжения в стержне при φmin=0,530