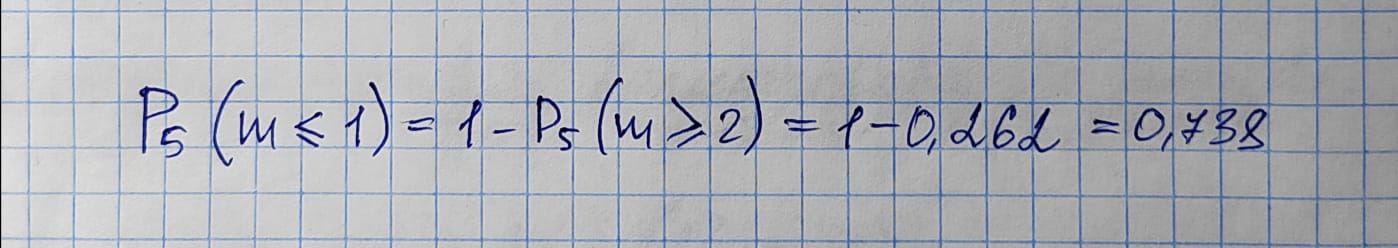Министерство науки и ВЫСШЕГО ОБРАЗОВАНИЯ Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уральский государственный экономический университет» (УрГЭУ)

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Математика»

Институт непрерывного и дистанционного образования Направление подготовки Управление качеством Направленность (профиль) Управление качеством в производственно-технологических системах и сфере услуг Кафедра __________________________________ Дата защиты: ________________ Оценка: ________________

Студент Суслова Дарья Андреевна Группа ИДО ЗБ УК-22 КЧ Руководитель Филиппов Сергей Дмитриевич

Екатеринбург

2023 г.
Вариант 7
Задача 1
Среди 17 студентов группы, из которых 8 – девушки, разыгрывается 7 билетов в театр. Какова вероятность того, что среди обладателей билетов окажутся 4 девушки и 3 юношей?
Решение:
Для определения количества возможных вариантов, соответствующих условиям задачи, изначально нужно определить число способов выбрать 7 студентов из 17:



 

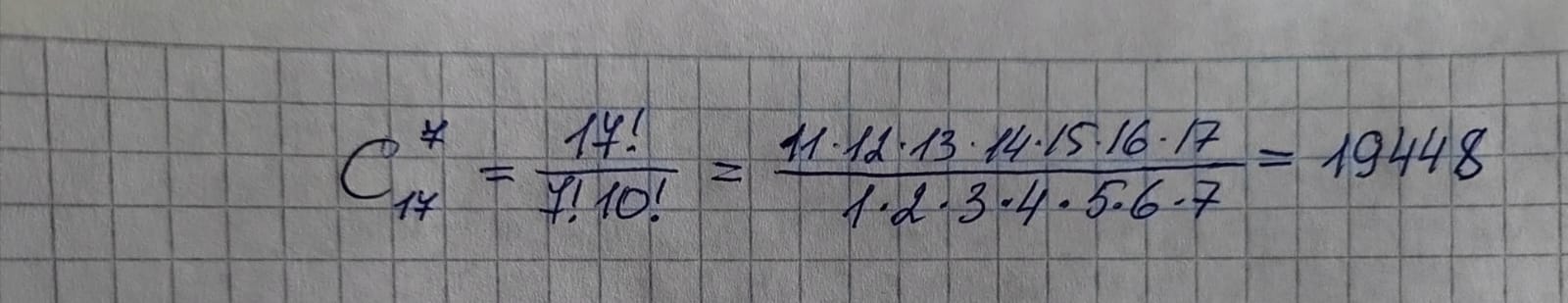
Из них благоприятных исходов (среди студентов выбираем 4 девушек из 8 и 3 мальчика из 9):

---

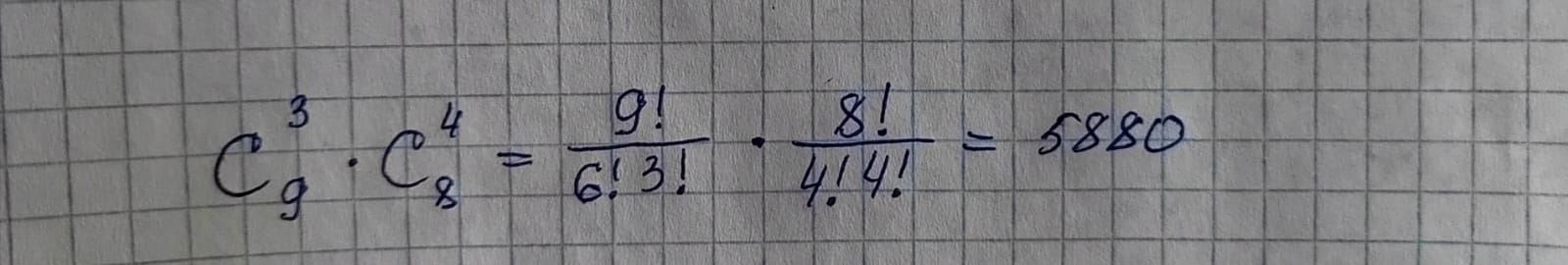
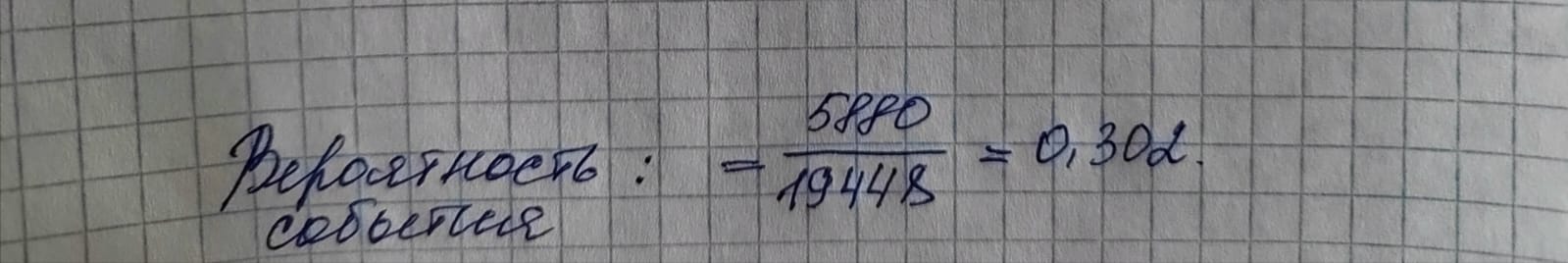
Ответ: Вероятность наступления события ровна 0,302.

Задача 2

Устройство состоит из трёх элементов, работающих независимо. Вероятности безотказной работы первого, второго и третьего элементов соответственно равны 0,6; 0,7; 08. Найти вероятность того, что безотказно будут работать: а) только один элемент; б) только два элемента; в) все три элемента.

Решение:

Найдем вероятность события (а), безотказно будет работать только один элемент:



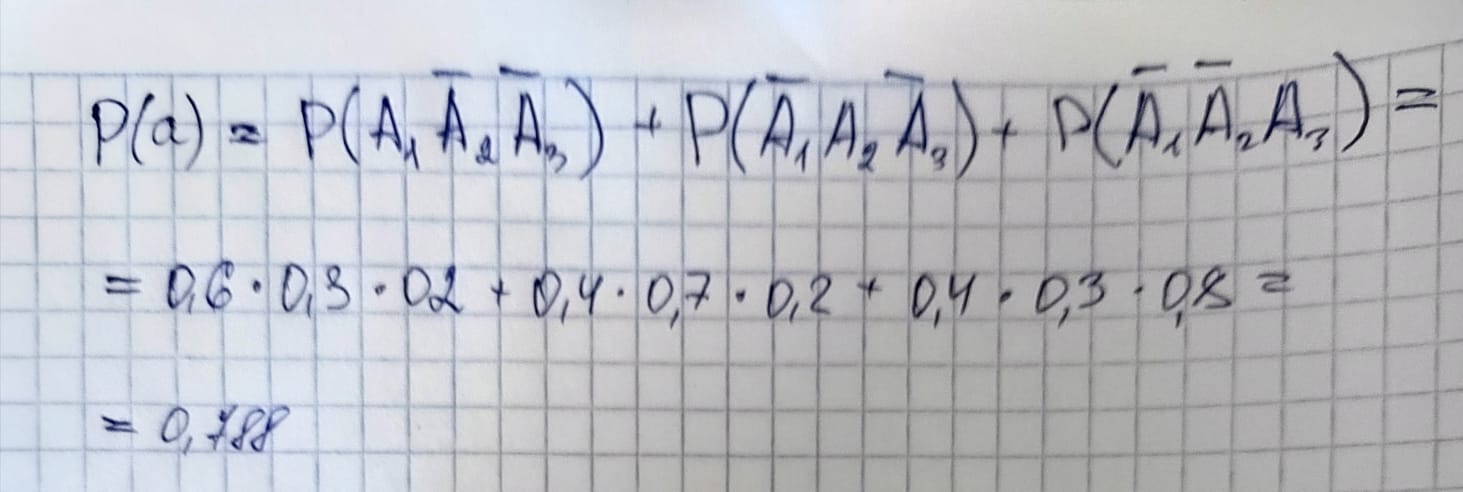
Найдем вероятность события (б), безотказно будет работать только два элемента



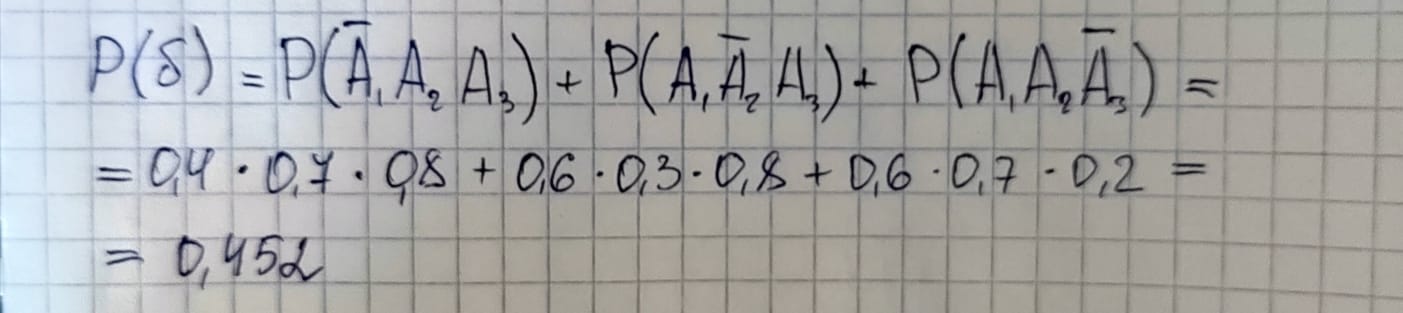
Найдем вероятность события (в), безотказно будет работать все три элемента:


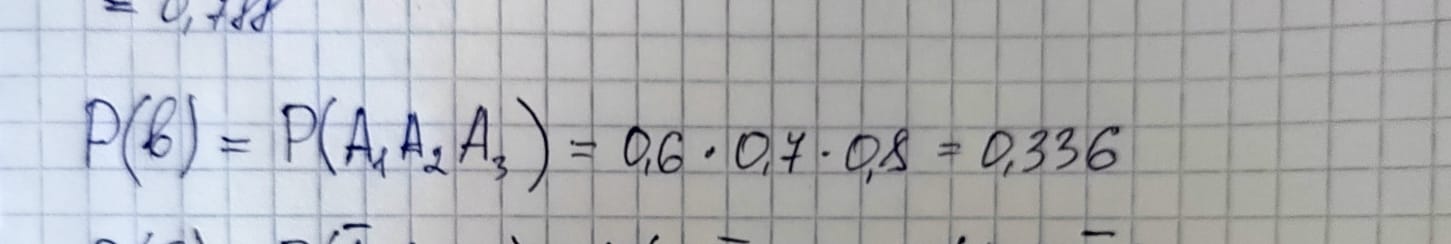
Задача 3

В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму для лыжника равна 0,9; для велосипедиста – 0,8; для бегуна – 0,75. Вызванный наудачу спортсмен норму выполнил. Найти вероятность того, что это бегун.

Решение:

Всего в группе 30 спортсменов, тогда:

Вероятность что выберут лыжника Р1=20/30=2/3

Вероятность что выберут велосипедиста Р2=6/30=1/5

Вероятность что выберут бегуна Р3=4/30=2/15

Вероятность того, что выбран лыжник и он выполнил норму: Р1*0,9=2/3*0,9=0,59

Вероятность того, что выбран велосипедист и он выполнил норму: Р2*0,8=1/5*0,8=0,16

Вероятность что выбран бегун и он выполнил норму: Р3*0,75 = 4/30*0,75=0,09

Так как эти события независимы, то вероятность того, что вызванный наудачу спортсмен норму выполнил ровна сумме всех трех вероятностей:

0,09+0,59+0,16=0,84

Задача 4

В магазине 5 холодильников. Вероятность выхода каждого холодильника из строя в течение года равна 0,2. Найти вероятность того, что в течение года ремонта потребует: а) ровно 4 холодильника; б) не менее 2 холодильников; в) не более 1 холодильника.

---

Решение:

Поскольку все холодильники имеют одинаковую вероятность выхода из строя в течении года р=0,2, то используем схему Бернулли:

Вероятность того, что ремонта потребуют 4 холодильника:



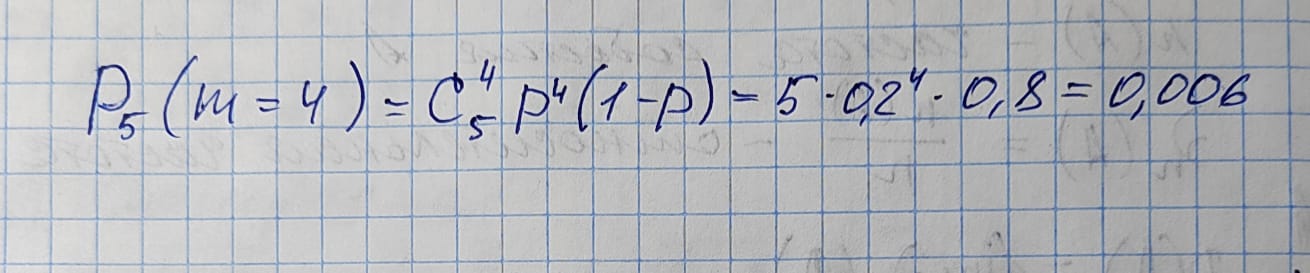
Вероятность того, что ремонта потребуют не менее 2 холодильников:



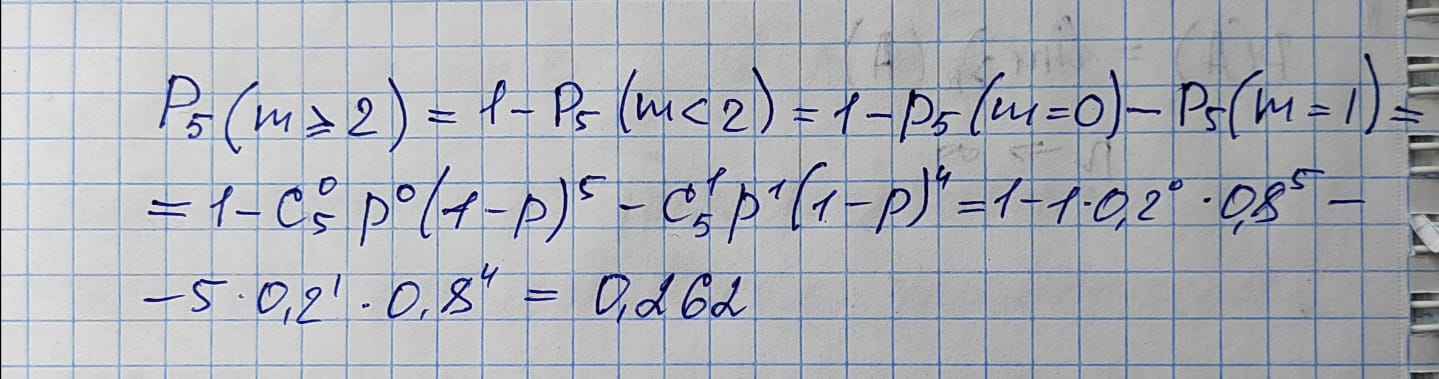
Вероятность того, что ремонта потребуют не более 1 холодильника:

---

Смотрите также файлы

• в некотором царстве в некотором государстве.docx

• Геологические и промысловые данные Приобское месторождения.docx

• Содержание Введение стр. 1 Метаморфизм.docx

• Metalworking forming processes.docx

• Инструкция по выполнению практической работы выберите класс, тему урока в соответствии с прп и заполните представленную ниже таблицу..docx