Файл: Скорость. Ускорение точки. Разложение полного ускорения на нормальное и тангенциальное.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Скорость. Ускорение точки. Разложение полного ускорения на нормальное и тангенциальное.
v - Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени; Вектором средней скорости (v)называется отношение приращения Аг радиуса-вектора точки к промежутку времени At; Мгновенная скорость v, таким образом, есть векторная величина, определяемая первой производной радиуса вектора движущейся точки по времени;
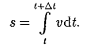 неравномерн.
неравномерн. 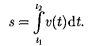 равноемерн
равноемерн
a -Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение; Средним ускорением неравномерного движения в интервале от t до t + A t называется векторная величина, равная отношению изменения скорости Av к интервалу времени At; Мгновенным ускорением а (ускорением) материальной точки в момент времени t будет предел среднего ускорения
Тангенциальное а - т.е. равна первой производной по времени от модуля скорости: она определяет быстроту изменения скорости по модулю Составляющая ускорения называется нормальной составляющей ускорения и направлена по главной нормали к траектории к центру еекривизны
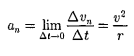
плоское а - Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих
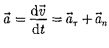
1) ат= 0, ап = О — прямолинейное равномерное движение;
2) ат= а — const, ап= 0 — прямолинейное равнопеременное движение
3) ат= f(t), ап= 0 — прямолинейное движение с переменным ускорением
4)ат— 0, ап= cons - по окружности
5) ат= 0, ап (не равн) 0 — равномерное криволинейное движение
6) ar = const, ап (не равн) 0 — криволинейное равнопеременное движение
7)ат= f(t), ап(не равн) 0 — криволинейноедвижение с переменным ускорением
-
Кинематические параметры вращательного движения: угловой путь, угловая скорость, угловое ускорение
Угловой скоростью называется векторная величина, определяемая первой производной угла поворота тела по времени; нейной скорости можно написать как векторное произведение v=wR; Если w = const, то вращение равномерное и его можно характеризовать периодом вращения Т; Частота вращения есть величина равная числу оборотов за единицу времени w=2Pn; Угловым ускорением называется векторная величина, определяемая первой производной угловой скорости по времени. Движение ускоренное - вектора совпадают, замедленное - противоположны.
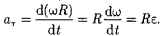
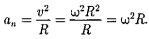
Угловой путь произведение средней угловой скорости на время
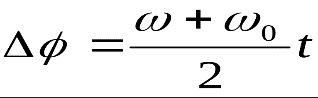
-
Законы Ньютона. Основное уравнение динамики поступательного движения.
Первый закон: Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. (закон инерции); Первый закон Ньютона утверждает существование инерциальных систем отсчета.
Второй закон: основной закон динамики поступательного движения — отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил; 2 ЗН - ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
Третий закон: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.
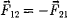
Основное уравнение динамики поступательного движения. Тела не входящие в состав рассматриваемой системы, называют внешними телами, а силы, действующие на систему со стороны этих тел, - внешними силами. Силы взаимодействия между телами внутри системы называют внутренними силами.
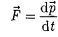
-
Закон сохранения импульса (формулировка, математическая запись, условия применимости)
импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени
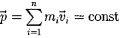
Закон сохранения импульса можно применять только тогда, когда система, для которой он записан, замкнута, то есть на нее не действуют внешние силы или они уравновешены, скомпенсированы.
Условия применимости:
-
Внешние силы уравновешивают друг друга или ими можно пренебречь
-
Проекция внешних сил на некоторую ось координат равна нулю
-
Удары, столкновения, разрывы, выстрелы
-
Момент силы, момент инерции тела, момент импульса тела относительно неподвижной точки, неподвижной оси.
Моментом силы относительно неподвижной точки О называется физическая величина М, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку Л приложения силы, на силу F
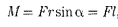
Моментом силы относительно неподвижной оси z называется скалярпая величина М,, равная проекции на эту ось вектора Л/момента силы, определенного относительно произвольной точки О данной оси z
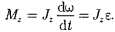
Моментом инерции системы (тела)относительно данной оси называется физическая величина, равная сумме произведений масс п материальных точек системы на квадраты их расстоянии до рассматриваемой оси
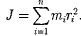 .
.
теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции Jс относительно параллельной оси, проходящей через центр масс С тела
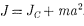
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением
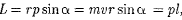
Моментом импульса относительно неподвижной оси z называется скалярная величина Lг , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси
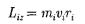
-
Закон динамики вращательного движения. Уравнение моментов. Закон сохранения момента импульса (формулировка, математическая запись, условия применимости).
Закон динамики вращательного движения 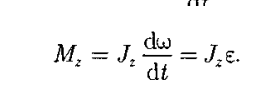 Уравнение представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Уравнение представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Уравнение моментов: производная момента импульса относительно некоторой точки равна суммарному моменту сил относительно той же точки, ˙ L = M.
З акон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени или Суммарный момент импульса тел образующих замкнутую систему остается неизменным при любых взаимодействиях между телами.
акон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени или Суммарный момент импульса тел образующих замкнутую систему остается неизменным при любых взаимодействиях между телами.
Условия применимости в незамкнутых системах моменты внешних сил скомпенсированы, внешние силы проходят через ось вращения.
-
Работа силы и момента силы. Механическая энергия. Кинетическая энергия тела при поступательном и вращательном движении.
-
Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол а с направлением перемещения, то работа этой силы равна произведению проекции силы Fs на направление перемещения (Fs = Fcos а), умноженной на перемещение точки приложения силы:
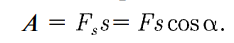
Моментом силы относительно неподвижной точки О называется физическая величина М, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку Л приложения силы, на силу F



-
Понятие потенциальной энергии. Закон сохранения механической энергии (формулировка, математическая запись, условия применимости).
Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем. Закон сохранения механической энергии можно сформулировать так: в консервативных системах полная механическая энергия сохраняется
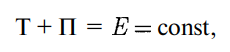
-
Уравнение Клапейрона – Менделеева. Основное уравнение молекулярно кинетической теории газов. Законы идеального газа (уравнение, графики процессов в координатах P-V).
Уравнение Клпейрона Менделеева


Закон Бойля — Мариотта1: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная:
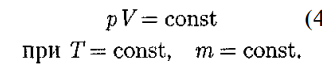
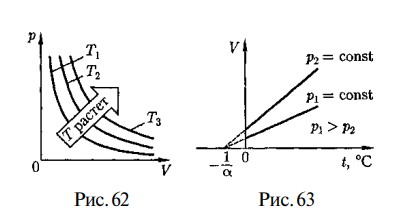
График зависимости между параметрами состояния газа при постоянной температуре называется изотермой. Изотермы в координатах р, V представляют собой гиперболы, расположенные на графике тем выше, чем выше температура, при которой происходит процесс (рис. 62). Законы Гей-Люссака2 :1) объем данной массы газа при постоянном давлении изменяется линейно с температурой:
В этих уравнениях t — температура по шкале Цельсия, р0 и Vo — давление и объем при 0°С, коэффициент а = 1/273,15 К- 1 . Процесс, протекающий при постоянном давлении, называется изобарным
На диаграмме в координатах V, t (рис. 63) этот процесс изображается прямой, называемой изобарой. Процесс, протекающий при постоянном объеме, называется изохорным. На диаграмме в координатах р, t (рис. 64) он изображается прямой, называемой изохорой. Из (41.2) и (41.3) следует, что изобары и изохоры пересекают ось температур в точке t= - -273,15 °С, а определяемой из условия 1 + at = 0. Если перенести начало отсчета в эту точку, то происходит переход к шкале Кельвина (см. рис. 64), откуда
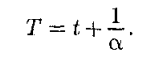
Вводя в формулы (41.2) и (41.3) термодинамическую температуру, законам Гей-Люссака можно придать более удобный вид:
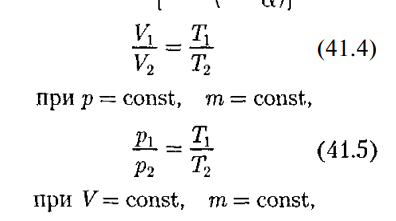
где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре. Закон Авогадрох \ 1 моль любого газа при одинаковых температуре и давлении занимает одинаковый объем. При нормальных условиях этот объем равен 22,41 • 1СГ3 м 3 /моль. По определению, 1 моль различных веществ содержит одно и то же число молекул, называемое постоянной Авогадро:
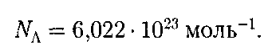
Закон Дальтона2 : давление смеси идеальных газов равно сумме парциальных давлений р1: р2 , ..., рп входящих в нее газов: P = Pl + P2 + ...+ РпПарциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.
-
Явления переноса (виды, определение, физические законы).
К явлениям переноса относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса)
1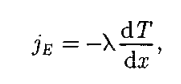
. Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т.е., иными словами, выравнивание температур. Перенос энергии в форме теплоты подчиняется закону Фурье:
где jE — плотность теплового потока — величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х; X — теплопровооность; 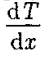 Градиент температуры
Градиент температуры
2. Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Явление диффузии для химически однородного газа подчиняется закону Фика:
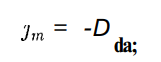 где j m — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х; D — диффузия (коэффициент диффузии); -
где j m — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х; D — диффузия (коэффициент диффузии); -
— граах диент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке.
-
Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Согласно формуле (31.1), сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона: 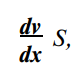 где т] — динамическая вязкость (вязкость); — градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев; S — площадь, на которую действует сила F.
где т] — динамическая вязкость (вязкость); — градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев; S — площадь, на которую действует сила F.
-
Работа газа. Количество теплоты. Внутренняя энергия идеального газа
П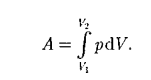 олную работу А, совершаемую газом при изменении его объема от Vx до V2 , найдем интегрированием формулы
олную работу А, совершаемую газом при изменении его объема от Vx до V2 , найдем интегрированием формулы
Удельная теплоемкость вещества — величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К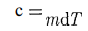
Внутренняя энергия идеального газа это сумма кинетических энергий движения молекул. Потенциальные энергии не учитываются, потому что газ является идеальным (не учитывается взаимодействие молекул). В случае с идеальным газом его внутренняя энергия зависит только от его температуры (закон Джоуля) и определяется по формуле:
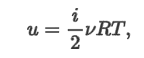

-
. Первое начало термодинамики. Применение первого начала к изопроцессам
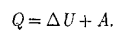 Уравнение выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил
Уравнение выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил

-
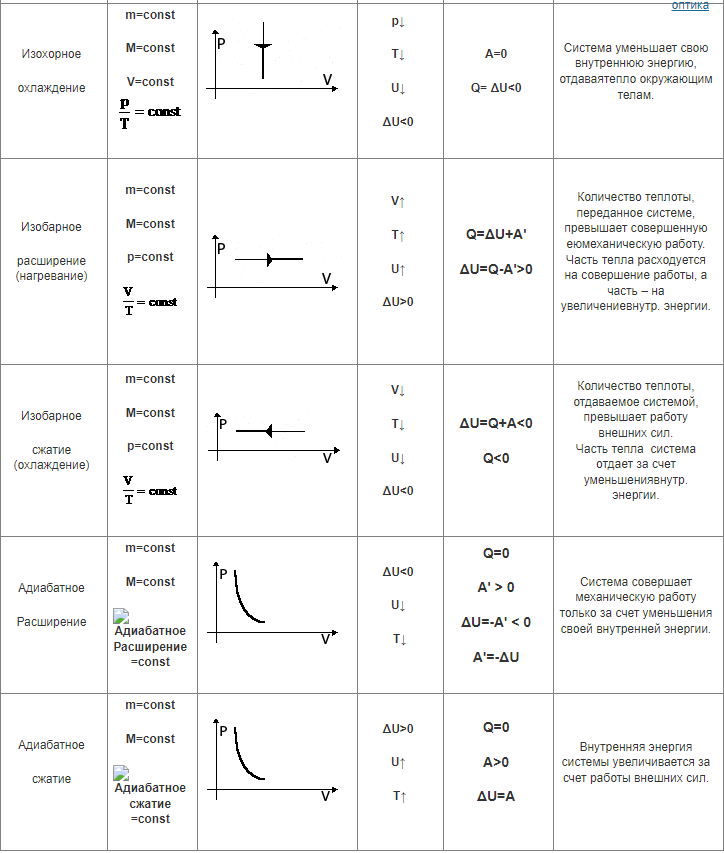
Адиабатный процесс
Адиабатным называется процесс, при котором отсутствует теплообмен между системой и окружающей средой (б Q = 0). К адиабатным процессам можно отнести все быстропротекающие процессы
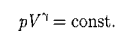 Полученное выражение есть уравнение адиабатного процесса, называемое также уравнением Пуассона
Полученное выражение есть уравнение адиабатного процесса, называемое также уравнением Пуассона
-
Цикл Карно и его КПД.
Цикл Карно — цикл, состоящий из четырех последовательных обратимых процессов: изотермического расширения, адиабатного расширения, изотермического сжатия и адиабатного сжатия
Прямой цикл Карно изображен на рис. 89, где изотермические расширение и сжатие заданы соответственно кривыми 1 — 2яЗ — 4, а адиабатные расширение и сжатие — кривыми 2—3 и 4—1.
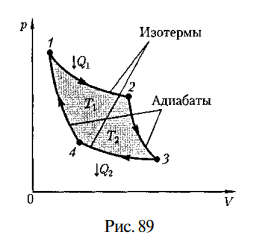
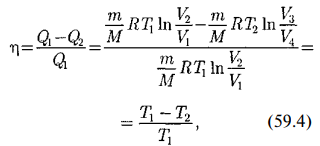
т. е. для цикла Карно КПД действительно определяется только температурами нагревателя и холодильника (доказательство теоремы Карно). Для повышения КПД необходимо увеличивать разность температур нагревателя PI холодильника
-
Электростатическое поле (ЭСП), его характеристики – напряженность, потенциал, разность потенциалов. Графическое изображение полей.
Электрические поля, которые создаются неподвижными электрическими зарядами называются электростатическими.
Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля
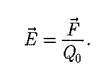
Как следует из формул (79.1) и (78.1), напряженность поля точечного заряда в вакууме
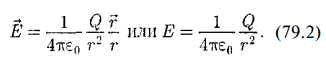
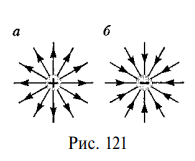
Графически электростатическое поле изображают с помощью линий напряженности — линии, касательные к которым в каждой точке совпадают с направлением вектора Ё (рис. 121).
Qa является энергетической характеристикой электростатического поля, называемой потенциалом
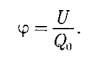
Потенциал ф в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку
Из формул (84.4) и (84.2) следует, что потенциал поля, создаваемого точечным зарядом Q, равен
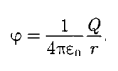
Работа, совершаемая силами электростатического поля при перемещении заряда QQ ИЗ ТОЧКИ 7 в точку 2 [см. (84.1), (84.4), (84.5)], может быть представлена как
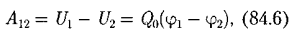
т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках
Разность потенциалов двух точек 1 в 2 в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного положительного заряда из точки 1 в точку 2.
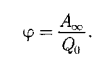
Таким образом, потенциал — физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки поля на бесконечность.
-
Поток напряженности электрического поля. Теорема Остроградского – Гаусса. Методы вычисления напряженности.
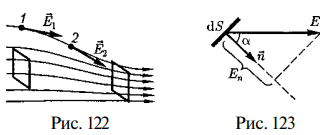
Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, условились проводить их с определенной густотой (рис. 122): число линий напряженности, пронизывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Е. Тогда число линий напряженности, пронизывающих элементарную площадку dS, нормаль пк которой образует угол а с вектором Ё, равно EdScos a
EndS, где Еп— проекция вектора Ё на нормаль п к площадке с!5'(рис. 123). Величина называется потоком вектора напряженности сквозь площадку dS. Здесь &S = dSn — вектор, модуль которого равен dS, а направление совпадает с направлением нормали п к площадке. Выбор направления вектора п (а следовательно, и dS) условен, так как его можно направить в любую сторону. Единица потока вектора напряженности электростатического поля — вольтметр (В • м).
-
Скорость. Ускорение точки. Разложение полного ускорения на нормальное и тангенциальное.
v - Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени; Вектором средней скорости (v)называется отношение приращения Аг радиуса-вектора точки к промежутку времени At; Мгновенная скорость v, таким образом, есть векторная величина, определяемая первой производной радиуса вектора движущейся точки по времени;
a -Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение; Средним ускорением неравномерного движения в интервале от t до t + A t называется векторная величина, равная отношению изменения скорости Av к интервалу времени At; Мгновенным ускорением а (ускорением) материальной точки в момент времени t будет предел среднего ускорения
Тангенциальное а - т.е. равна первой производной по времени от модуля скорости: она определяет быстроту изменения скорости по модулю Составляющая ускорения называется нормальной составляющей ускорения и направлена по главной нормали к траектории к центру еекривизны
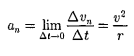
плоское а - Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих
1) ат= 0, ап = О — прямолинейное равномерное движение;
2) ат= а — const, ап= 0 — прямолинейное равнопеременное движение
3) ат= f(t), ап= 0 — прямолинейное движение с переменным ускорением
4)ат— 0, ап= cons - по окружности
5) ат= 0, ап (не равн) 0 — равномерное криволинейное движение
6) ar = const, ап (не равн) 0 — криволинейное равнопеременное движение
7)ат= f(t), ап(не равн) 0 — криволинейноедвижение с переменным ускорением
-
Кинематические параметры вращательного движения: угловой путь, угловая скорость, угловое ускорение
Угловой скоростью называется векторная величина, определяемая первой производной угла поворота тела по времени; нейной скорости можно написать как векторное произведение v=wR; Если w = const, то вращение равномерное и его можно характеризовать периодом вращения Т; Частота вращения есть величина равная числу оборотов за единицу времени w=2Pn; Угловым ускорением называется векторная величина, определяемая первой производной угловой скорости по времени. Движение ускоренное - вектора совпадают, замедленное - противоположны.
Угловой путь произведение средней угловой скорости на время
-
Законы Ньютона. Основное уравнение динамики поступательного движения.
Первый закон: Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. (закон инерции); Первый закон Ньютона утверждает существование инерциальных систем отсчета.
Второй закон: основной закон динамики поступательного движения — отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил; 2 ЗН - ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
Третий закон: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.
Основное уравнение динамики поступательного движения. Тела не входящие в состав рассматриваемой системы, называют внешними телами, а силы, действующие на систему со стороны этих тел, - внешними силами. Силы взаимодействия между телами внутри системы называют внутренними силами.
-
Закон сохранения импульса (формулировка, математическая запись, условия применимости)
импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени
Закон сохранения импульса можно применять только тогда, когда система, для которой он записан, замкнута, то есть на нее не действуют внешние силы или они уравновешены, скомпенсированы.
Условия применимости:
-
Внешние силы уравновешивают друг друга или ими можно пренебречь -
Проекция внешних сил на некоторую ось координат равна нулю -
Удары, столкновения, разрывы, выстрелы
-
Момент силы, момент инерции тела, момент импульса тела относительно неподвижной точки, неподвижной оси.
Моментом силы относительно неподвижной точки О называется физическая величина М, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку Л приложения силы, на силу F
Моментом силы относительно неподвижной оси z называется скалярпая величина М,, равная проекции на эту ось вектора Л/момента силы, определенного относительно произвольной точки О данной оси z
Моментом инерции системы (тела)относительно данной оси называется физическая величина, равная сумме произведений масс п материальных точек системы на квадраты их расстоянии до рассматриваемой оси
теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции Jс относительно параллельной оси, проходящей через центр масс С тела
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением
Моментом импульса относительно неподвижной оси z называется скалярная величина Lг , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси
-
Закон динамики вращательного движения. Уравнение моментов. Закон сохранения момента импульса (формулировка, математическая запись, условия применимости).
Закон динамики вращательного движения
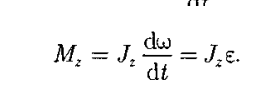 Уравнение представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Уравнение представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси. Уравнение моментов: производная момента импульса относительно некоторой точки равна суммарному моменту сил относительно той же точки, ˙ L = M.
З
Условия применимости в незамкнутых системах моменты внешних сил скомпенсированы, внешние силы проходят через ось вращения.
-
Работа силы и момента силы. Механическая энергия. Кинетическая энергия тела при поступательном и вращательном движении. -
Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол а с направлением перемещения, то работа этой силы равна произведению проекции силы Fs на направление перемещения (Fs = Fcos а), умноженной на перемещение точки приложения силы:
Моментом силы относительно неподвижной точки О называется физическая величина М, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку Л приложения силы, на силу F



-
Понятие потенциальной энергии. Закон сохранения механической энергии (формулировка, математическая запись, условия применимости).
Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем. Закон сохранения механической энергии можно сформулировать так: в консервативных системах полная механическая энергия сохраняется
-
Уравнение Клапейрона – Менделеева. Основное уравнение молекулярно кинетической теории газов. Законы идеального газа (уравнение, графики процессов в координатах P-V).
Уравнение Клпейрона Менделеева



Закон Бойля — Мариотта1: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная:
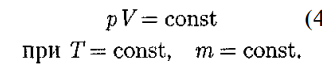
График зависимости между параметрами состояния газа при постоянной температуре называется изотермой. Изотермы в координатах р, V представляют собой гиперболы, расположенные на графике тем выше, чем выше температура, при которой происходит процесс (рис. 62). Законы Гей-Люссака2 :1) объем данной массы газа при постоянном давлении изменяется линейно с температурой:
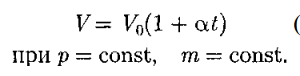
В этих уравнениях t — температура по шкале Цельсия, р0 и Vo — давление и объем при 0°С, коэффициент а = 1/273,15 К- 1 . Процесс, протекающий при постоянном давлении, называется изобарным

На диаграмме в координатах V, t (рис. 63) этот процесс изображается прямой, называемой изобарой. Процесс, протекающий при постоянном объеме, называется изохорным. На диаграмме в координатах р, t (рис. 64) он изображается прямой, называемой изохорой. Из (41.2) и (41.3) следует, что изобары и изохоры пересекают ось температур в точке t= - -273,15 °С, а определяемой из условия 1 + at = 0. Если перенести начало отсчета в эту точку, то происходит переход к шкале Кельвина (см. рис. 64), откуда
Вводя в формулы (41.2) и (41.3) термодинамическую температуру, законам Гей-Люссака можно придать более удобный вид:
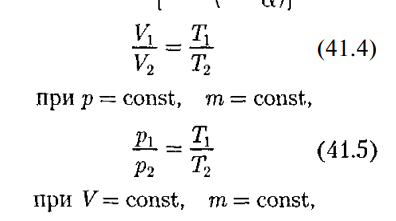
где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре. Закон Авогадрох \ 1 моль любого газа при одинаковых температуре и давлении занимает одинаковый объем. При нормальных условиях этот объем равен 22,41 • 1СГ3 м 3 /моль. По определению, 1 моль различных веществ содержит одно и то же число молекул, называемое постоянной Авогадро:
Закон Дальтона2 : давление смеси идеальных газов равно сумме парциальных давлений р1: р2 , ..., рп входящих в нее газов: P = Pl + P2 + ...+ РпПарциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.
-
Явления переноса (виды, определение, физические законы).
К явлениям переноса относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса)
1
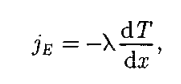
. Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т.е., иными словами, выравнивание температур. Перенос энергии в форме теплоты подчиняется закону Фурье:
где jE — плотность теплового потока — величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х; X — теплопровооность;
2. Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Явление диффузии для химически однородного газа подчиняется закону Фика:
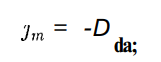 где j m — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х; D — диффузия (коэффициент диффузии); -
где j m — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х; D — диффузия (коэффициент диффузии); -Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Согласно формуле (31.1), сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:
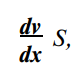 где т] — динамическая вязкость (вязкость); — градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев; S — площадь, на которую действует сила F.
где т] — динамическая вязкость (вязкость); — градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев; S — площадь, на которую действует сила F.Работа газа. Количество теплоты. Внутренняя энергия идеального газа
. Первое начало термодинамики. Применение первого начала к изопроцессам
Адиабатный процесс
Цикл Карно и его КПД.
Электростатическое поле (ЭСП), его характеристики – напряженность, потенциал, разность потенциалов. Графическое изображение полей.
Поток напряженности электрического поля. Теорема Остроградского – Гаусса. Методы вычисления напряженности.
В соответствии с формулой (79.3) поток вектора напряженности сквозь сферическую поверхность радиуса г, охватывающую точечный заряд Q, находящийся в ее центре (рис. 126), равен
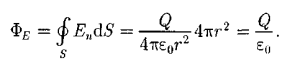
Этот результат справедлив для замкнутой поверхности любой формы.
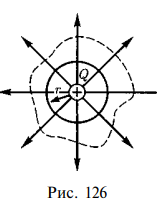
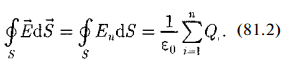
Формула (81.2) выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной па е0 . Эта теорема выведена математически для векторного поля любой природы русским математиком М. В. Остроградским (1801-1862), а затем независимо от него применительно к электростатическому полю — К. Гауссом
-
Условия равновесия зарядов в проводнике. Распределение избыточных зарядов на поверхности проводника. Проводники во внешнем электростатическом поле.
Равновесие зарядов на проводнике может наблюдаться при выполнении условий:
1. Напряженность поля всюду внутри проводника должна быть равна нулю E=0 (φ=const).
2. Напряженность поля на поверхности проводника должна быть в каждой точке направлена по нормали к поверхности E=En. Следовательно, при равновесии зарядов поверхность проводника будет эквипотенциальной
Распределение избыточных зарядов на поверхности проводника
Всякий процесс заряжения сводится к разделению зарядов, при котором на одном из тел (или части тела) появляется избыток положительного заряда, а на другом (или другой части тела) — избыток отрицательного заряда.
Общее количество зарядов обоих знаков, содержащихся в телах, не изменяется: эти заряды только перераспределяются между телами
Проводники во внешнем электростатическом поле
Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться. Перемещение зарядов (ток) продолжается до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль.
-
Электроемкость проводника, конденсатора. Емкость конденсатора, системы конденсаторов
Величину
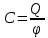
называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
Емкость конденсатора
Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов между его обкладками:
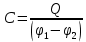
-
Энергия заряженного проводника и конденсатора. Энергия ЭП.
Плотность энергии ЭП
Энергия заряженного уединенного проводника
Пусть имеется уединенный проводник, заряд, емкость и потенциал которого соответственно равны Q, С, ф. Увеличим заряд данного проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности па уединенный проводник, затратив на это работу
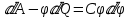
Чтобы зарядить тело от нулевого потенциала до ф, необходимо совершить работу
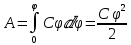
Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник
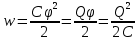
Энергия заряженного конденсатора
Как всякий заряженный проводник, конденсатор обладает энергией, которая в соответствии с формулой равна

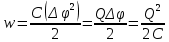
где Q — заряд конденсатора; С — его емкость; ▲ф — разность потенциалов между обкладками конденсатора.
Энергия ЭП
Энергия электростатического поля. Преобразуем формулу
w=C(Δφ^2 )/2=QΔφ/2=Q^2/2C
выражающую энергию плоского конденсатора посредством зарядов и потенциалов, воспользовавшись выражением для емкости плоского конденсатора
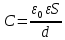 и разности потенциалов между его обкладками
и разности потенциалов между его обкладками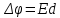
Тогда
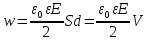
где V = Sd — объем конденсатора.
Плотность энергии ЭП
плотность энергии электростатического поля (энергия единицы объема)
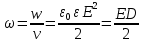
Это выражение справедливо только для изотропного диэлектрика, для которого выполняется соотношение:
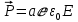
-
Закон Ома для однородного и неоднородного участка цепи. Закон Ома в дифференциальной форме. Работа постоянного тока в проводнике. Мощность. Закон Джоуля – Ленца в дифференциальной форме
Закон Ома для однородного участка цепи
Сила тока I, текущего по однородному металлическому проводнику (т.е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника
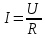
где R — электрическое сопротивление проводника.
Закон Ома для неоднородного участка цепи:
закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома.
Если на данном участке цепи источник тока отсутствует (ℰ12 — 0), то
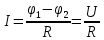
Выражение
закон Ома в дифференциальной форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке.
-
Законы Фарадея для электролиза
Первый закон Фарадея: Масса вещества, выделившегося на электроде при электролизе, пропорциональна количеству заряда, прошедшего через электролит:
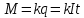
Где k-электрохимический эквивалент; I-сила тока; t-время
Второй закон Фарадея.Электрохимический эквивалент пропорционален молярной массе А иона и обратно пропорционален его валентности Z
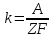
Тогда, подставив в формулу М=kIt, получим:
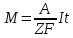
F=96500 Кл/моль -постоянная фарадея.
-
Газовый разряд. Типы самостоятельного разряда (особенности).
Газовый разряд-это процесс прохождения электрического тока через газ
Типы разрядов:
-
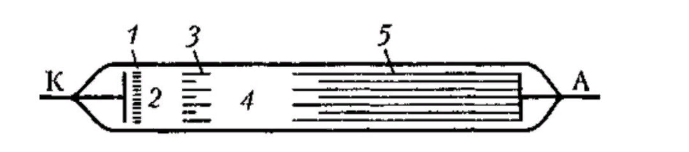
Тлеющий(возникает при низких давлениях)
-
Катодное свечение, катод -
Темное пространство -
Тлеющее свечение -
Фарадеево пространство -
Положительный столб
Применение:
-
Лампы дневного света -
Катодное напыление
-
Искровой(возникает при больших напряженностях электрического поля в газе)
Имеет вид светящегося темного канала изогнутого и разветвленного.
Применение:
-
Воспломинение горючей смеси -
Искровые разрядники -
Резка, сверление металла
3)Дуговой (возникает после искрового разряда, при сближении электронов)
Дуговой разряд можно получить от источника низкого напряжения, минуя стадию искры.
Дуговой разряд поддерживается за счет высокой температуры катода изза интенсивной термоэлектронной эмисии
Применение:
-
Сварка -
Кварцевая лампа
Умение проводить эксперимент и обрабатывать результаты эксперимента.
1 Измерением называют нахождение значения физической величины опытным путѐм с помощью технических средств. В прямых измерениях величину определяют непосредственно по шкале прибора, например, секундомера при измерении времени или амперметра при измерении тока. В косвенных измерениях результат вычисляют по формулам, используя данные прямых измерений.
2 Точность измерения величины x определяют по абсолютной или относительной погрешности Абсолютная погрешность Δx измеряемой величины равна разности измеренного x и истинного значения X, которое, конечно, неизвестно
Точность измерения оценивают по относительной погрешности. Относительная погрешность δx равна отношению абсолютной погрешности к истинному значению измеряемой величины:
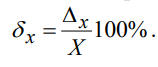
3 Класс точности прибора показывает относительную предельную погрешность (в %) для наибольшего измеряемого значения, равного пределу шкалы Xmax :
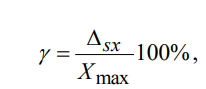
где sx –абсолютная предельная погрешность измеряемой величины X
Если класс точности и паспортные данные прибора неизвестны, то приборную погрешность принимают равной цене деления шкалы.