Файл: Алгебраны оытуды дістсілдеріжаашыл кзарас (GeoGebra жобасында).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Алгебраны оқытудың әдіс-тәсілдері-жаңашыл көзқарас
(GeoGebra жобасында)
Түйінді сөздер: алгебра, математика, математикалық ойлау, алгебралық ойлау, математиканы оқыту, негізгі мектеп, теңдеулер, алгебралық белгілер, оқыту әдістемесі, оқыту әдістері, эвристикалық әдіс. Алгебраны зерттеудің мақсаты белгілі бір математикалық фактілерді егжей-тегжейлі қарастыру ғана емес, сонымен бірге математика әдісін шұғыл қажеттілік туындаған кезде ғылымның басқа салаларында қолдана білу.
Мақаламызда мектептерде алгебраны оқытуға қатысты сұрақтарды қарастырғымыз келеді. Қазіргі уақытта алгебра пәнін оқытуды қанағаттанарлық деп санауға болмайтындықтан: әрбір сабақта дерлік күн тәртібі басым, ал математика педагогикасындағы жаңа тенденциялар бірінші кезеңде алгебраны оқыту саласында мектепке тым аз әсер етті. Мақалада алгебраны оқытудың негізгі әдістері мен тәсілдері көрсетілген: ғылыми-педагогикалық, көрнекі зертханалық, лекциялық және эвристикалық, сонымен қатар аудиториялық және сабақтан тыс зертханалық және практикалық сабақтар. Математикалық фактілердің өзін зерттеуден әлдеқайда маңыздысы – математика сабағында оқушыларды ойлаудың ең айқын, типтік және қарапайым әдістерімен таныстыру. Алгебраны оқытудың ресми мақсатын көздей отырып, біз оқушылардың ой-өрісін дамытатынымыз сөзсіз. Практикалық мақсатты көздей отырып, біз оларды алған ақпаратты практикалық білімде саналы және дұрыс қолдануға дағдыландырамыз. Мақсаттардың бірі – қысқаша алгебралық тілді дамыту. Алгебра осы арифметикалық амалдардың барлық ресми заңдарын тұрақты сақтай отырып, арифметикалық амалдарды кеңейтеді.Математиканы оқытудың ғылыми-педагогикалық әдісі. Алгебраны оқытудың әдіс-тәсілдері туралы сөз қозғағанда, бұл жағдайда жеке тұлғаның жан-жақты дамуы принципі ерекше мәнге ие болатынын, әрине, есте ұстаған жөн. Оқытудың мақсатқа сай әдісі оқушыны білімді берік және жылдам меңгеруге жетелейтін, оның қабілетін барынша жан-жақты және жан-жақты дамытуға жетелейтін әдіс ретінде ғана танылуы мүмкін және танылуы керек. Осындай өзіне тән ерекшеліктері бар әдіс әсіресе математиканы, оның ішінде алгебраны оқытуда білім алатын жеке тұлғаларды, олардың даму дәрежесі мен барысын, сондай-ақ олардың өмірлік қажеттіліктері мен жеке ерекшеліктерін үнемі назарда ұстауды ұсынады. Педагогикалық әдістің ғылыми әдістен айырмашылығы неде және олардың әрқайсысына тән белгілер қандай? Ғылыми әдіс 2 түрде көрінеді: бұл әдістің 1-ші түрі әлі белгісіз шындықтарды зерттеу немесе ашу әдісінен басқа ештеңе емес; Оның 2-ші түрі - бірінші әдіспен алынған шындықты көрсету әдісі. Ғылыми әдістің екі формасының арасында маңызды айырмашылық жоқ екенін есте сақтай отырып, біз ашу әдісі мен экспозиция әдісінің белгілі бір ерекше айырмашылығы бар екенін есте ұстауымыз керек, ол жаңа идеяның кез келген ашылуына байланысты. жүйелі түрде жүзеге асырылмайды, бірақ азды-көпті кездейсоқ және кенеттен жүреді, ал ғылыми экспозицияда айтылған ойларды жүйелеуге толық мүмкіндігі бар, оларды бір-бірімен салыстыру, сол арқылы олардың мәнін тауып, анықтау мүмкіндігі бар.Бұл жағдайда қарастырылып отырған ғылыми әдістің нысаны, экспозиция әдісі таза педагогикалық әдіске өте жақын болуы мүмкін. Педагогикалық әдіс ашу немесе зерттеу әдісі емес, баяндау әдісі болып табылады және ол ғылыми баяндау әдісінен өзінің элементарлылығымен және ішкі жағынан айқындылығымен, сондай-ақ сыртқы жағынан көрнекілігімен және сұрақ-жауап формасымен ерекшеленеді. Математика мұғалімі, әрине, түсіндірілген ғылымды терең және жан-жақты білуі және оқушылардың психологиясын және оларға берілген белгілі бір математикалық білімдерді олардың тәрбиелеу және меңгеру заңдылықтарын білуі қажет. Мектепте мұғалім-математик өз оқушыларына алгебраны ғылыми тұрғыдан мінсіз түсіндіретін және сонымен бірге тіпті әлсіз оқушылар ұсынған материалды сөзсіз меңгеруге табанды түрде қол жеткізетін әдіс қана орынды. Ғылыми-педагогикалық әдістің 2 негізі бар, атап айтқанда: 1) объективті қызығушылық, яғни ұсынылатын пәннің қызығушылығы және 2) субъективті қызығушылық, яғни оқушылардың қызығушылығы және осы екі негіз, әрине, бірдей маңызды деп танылуы керек, нәтижесінде алгебраны оқытуда олардың екеуі де бірдей дәрежеде қанағаттандырылуы керек.
Пәнді жақсы ғылыми-педагогикалық баяндау үшін мұғалімге тиісті ғылымды жетік білу қажет, ал оған балалардың психикалық дамуын дұрыс түсінуі кем емес, ең өзіне тән дәуірлерді ескеру қажет. Оқушылардың ой-өрісін дамытуда оқыту барысында оқушылардың әр түрлі жеке ерекшеліктеріне қарай қолдану қажет, яғни мұғалім оқытылатын ғылымды және оқушылардың психологиясын білуі қажет. Оқушыларға сол немесе басқа оқу пәндерінен білім берудің дұрыс емес тәсілі, яғни оқытудың субъективтік жағын үзілді-кесілді елеусіз қалдыру, тек бір объективті жағын табанды түрде есте ұстау. Көрнекі-зертханалық әдіс және алгебраны оқыту әдістемесі. Оқу материалын тарату жолдарын көрсетуге келгенде немесе оны оқыту әдістемесіне байланысты дамыту әдістері туралы айтқанда, әдіс сөзі қолданылады. Олар оқушыларға пәнді оқытудың немесе ұсынудың ең айқын тәсілдерін ғана білдіретін жағдайларда қабылдау терминін қолдану әдеттегідей. Алгебраны оқытқанда мұғалім бір жағынан ғылымның немесе пәннің мүддесі мен дамуын, екінші жағынан жеке тұлғаның дамуын міндетті түрде ескеруі керек. Бұл негіздер мұғалімнің оқуды көрнекі-зертханалық әдіспен жүргізуге итермелейді. Өйткені алгебраның даму тарихы абстрактілі тұжырымдар мен формулалар түрінде пайда болған жоқ, дәл жеке көрнекі фактілерді жинақтап, біріктіруден басталды.Оқытудың көрнекі әдісімен мұғалім ұсынылатын ғылымның немесе пәннің мазмұнын бірнеше қарапайым элементтерге ыдыратуы керек, содан кейін осы элементтерден міндетті түрде оқуды бастағаннан кейін, оқушыларды жүйелі түрде қарастыруға бағыттау керек. таңдалған элементтердің азды-көпті күрделі түзілімдерге қосылуы. Оқытудың көрнекі әдісі 2 негізге, яғни сыртқы көрнекілікке және элементарлық деп аталатынға негізделуі керек және көрнекілік пен элементарлық табиғат бір-бірімен дұрыс және берік үйлескенде ғана ол көрнекілік оқыту әдісін құрайды. Көрнекі оқыту, әрине, әр адамға сенсорлық материалдың кез келген түрінен бейнелеуді құруға мүмкіндік беретін бейнелеу түрлерін ескереді. Кез келген жаттығу адамды стихиялық әрекетке ынталандыруы керек. Математика ғылымдарын оқыту әдістемесі өз мәні бойынша аналитикалық әдіс болып табылады. Абстрактілі немесе абстрактілі математикаға көшу табиғи жолмен жүзеге асырылуы керек, яғни ол нақты математикадан шығуы керек, нәтижесінде геометрияны зерттеу де алгебра сабақтарында оқудан бұрын болуы керек, бірақ ол оқудан да бұрын болуы керек. Арифметика және бөлгіштер теориясы сабақтарында, әрине, бөлшектер мен пропорцияларды зерттеуден бұрын болуы керек. Бұл, жалпы алғанда, оқытудың көрнекі әдісі мәселесі бойынша эксперименттік-педагогикалық пайымдаулар. Тренинг арқылы берілетін барлық жаңа қабылдаулар мен көріністер белсенділікке өтуі керек.Қолданыстағы оқу бағдарламалары мен қолданбалы оқыту әдістерінің басты қателігі – бақылауға негізделген материалды оқыту мен іс-әрекетке негізделген кескіндемелік немесе формалды оқыту арасындағы тығыз байланыстың, өзара әрекеттестіктің және өзара түсіністіктің болмауы. Оқушыға бере алатын ең құнды нәрсе – бұл мүлде білім емес, тек білім алудың дұрыс әдісі және өз бетінше әрекет ету тәсілі. Көрнекі-зертханалық әдісті жалпы түрде қарастырайық. Математика сабағында бұл әдістің негізгі мәні неде екенін анықтауға тырысайық? Алгебралық жұмыстың негізгі бөлігі сыныпта, барлық оқушылар бір мезгілде және сонымен қатар мұғалімнің тікелей, тәжірибелі басшылығымен жүргізілетінін қатаң сақтау қажет. Алгебралық сұрақтарды олардың дамуының әртүрлі кезеңдерінде зерттеңіз және графикалық және эксперименталды түрде зерттеңіз, бірақ әрқашан нақты есептер немесе мысалдар бойынша. Абстрактілі оқыту да көрнекі болуы мүмкін. Бүтін сандар алдымен нақты мысалдармен түсіндірілмейінше, мағынасы болмайды. Оқушы оларды меңгерген кезде олар нақтылыққа ие болады және олар оқушыны жаңа алаңдататын нәрселерге жетелеу үшін пайдаланылуы мүмкін. Бұл, жалпы алғанда, ғылыми-педагогикалық баяндау әдістерінің сыртқы белгілері. Бұл әдістердің ішкі жағына келетін болсақ. Эвристикалық әдістің ішкі жағын қарастыруға келер болсақ, ең алдымен оқытудың эвристикалық әдісінің жеке әдіспен ең тығыз байланысы бар жағдайды атап өту керек, егер соңғысын мынадай бар әдіс деп түсінсек. оның негізгі мақсаты сынып жұмысын ұйымдастыру. Әрбір жеке оқушы мұғалімнің қойған сұрақтарына жауап беріп, алдына қойылған мүмкін тапсырмаларды орындай отырып, өзінің жеке қабілетіне сай дамып, алға жылжуы үшін. Геогебра жүйесін қолдану арқылы есептерді шешу бойынша әдістемелік ұсыныстар талданады. Біз GeoGebra бағдарламасын сабақта қолдану мыналарға мүмкіндік беретінін анықтадық:
- сабақтың әртүрлі кезеңдерінде уақытты ұтымды пайдалана отырып, оқу процесін оңтайландыру;
− оқытудың сараланған тәсілін енгізу;
− дербес компьютерлерді пайдалана отырып, жеке жұмыстарды орындау;
- ойынның бір элементін енгізу арқылы сабақтағы эмоционалды стрессті азайту;
- оқушылардың ой-өрісін кеңейту;
- оқушылардың танымдық белсенділігін дамытуға ықпал етеді. Бұл жүйені сабақта қолданудың болжамды әсерлері
математика:
- үлгерімі нашар оқушылардың оқытылатын пәнге деген қызығушылығын арттыруға болады;
−өзін-өзі бағалау деңгейін арттыру;
− өзін-өзі бақылау дағдыларын дамыту;
- ақпараттық технология саласында жаңа нәрселерді ашуға және зерттеуге ынта, өз білімін жолдастарымен бөлісуге ұмтылу.
Практикалық бөлім:
Теңдеуді шешу үшін қажет болсын: 8x3 6x 1 0
Бұл теңдеуді әртүрлі тәсілдермен шешудің сәтсіз әрекеттерінен кейін (бүтін санды / рационал түбірді болжау, факторинг және т.б.) оқушыларға осы теңдеудің сол жағын салу үшін GeoGebra-ды пайдалануды ұсынамыз. Функцияның графигін алыңыз (суретте көрсетілген).
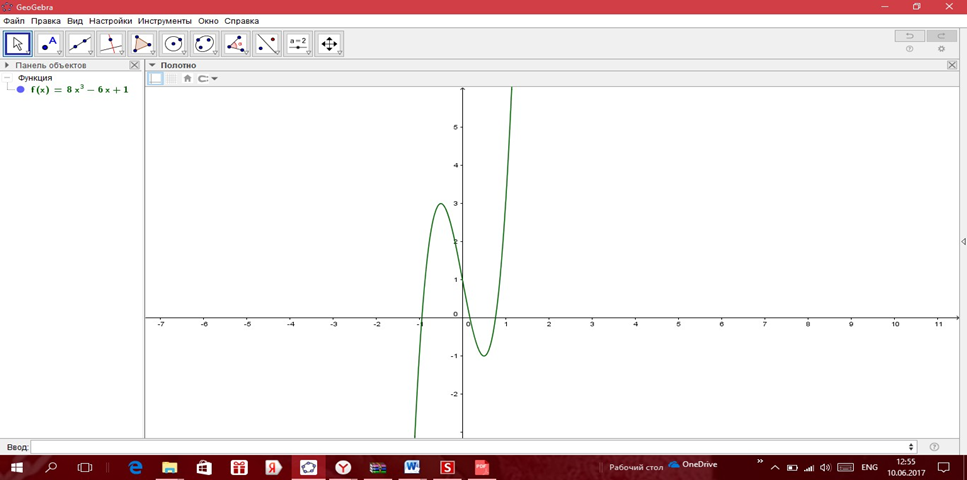
Мұндағы «компьютерлік пайымдау» келесі дедуктивті пайымдауды алға шығару үшін графикалық демонстрация ретінде қызмет етеді:
- функция графигінің абсциссамен қиылысуының барлық нүктелері (-1; 1) интервалында болғандықтан, бұл теңдеудің барлық түбірлері абсолютті мәнде 1-ден кіші;
- өйткені теңдеудің барлық түбірлері абсолютті мәнде 1-ден аз және (0; π) аралықтағы бұрыштардың косинустарының барлық мәндері (аралық бұрыштардың синусы)
Жоғарыда келтірілген мысал «компьютерлік негіздеу» таза алгебралық негіздемеден айырмашылығы, студенттерді мұндай ауыстырудың «табиғидығына» сендіріп қана қоймай, сонымен қатар оның қажеттілігінің себебін ашатынын көрсетті. Мұндай оң әсерге осы теңдеудің графикалық интерпретациясының арқасында қол жеткізіледі.
Дегенмен, «компьютерлік негіздеу» алгебралық негізді алмастыра алмайды дегенге сенбейміз. Біріншіден, математикалық талдау әдістерін қолдана отырып, оны құрудың дұрыстығын тексеруге қарағанда, Геогебра SCA көмегімен функция графигін салудың дұрыстығын дәлелдеу бірнеше шама ретті болғандықтан қиынырақ. Екіншіден, бұл негіздемелер әртүрлі білім беру функцияларына ие:
- «компьютерлік негіздеу» оқушыларды теңдеудің графикалық интерпретациясын көрсету арқылы айнымалыны өзгерту идеясына әкеледі;
- алгебралық негіздеу функцияның графигі мен теңдеудің түбірлері арасындағы байланысты орнату арқылы мұндай ауыстырудың қажеттілігін дәлелдейді.
Стандартты емес теңдеулерді шешуді оқытуда SCA GeoGebra қолдану «компьютерлік негіздеуден» алгебралық әдіске көшу процесі болып табылады.
Бұл ретте GeoGebra көмегімен стандартты емес теңдеулерді шешу дағдыларының екі түрлі деңгейінің болуы туралы айтуға болады.
I. Эмпирикалық деңгей көз жеткізу қабілетімен ерекшеленеді
функцияның графигін салу үшін қолданылатын GeoGebra көмегімен теңдеуді шешудің таңдалған әдісін «табиғи» қолдану.
II. Абстрактілі-теориялық деңгей GeoGebra SCA көмегімен алынған функция графигінің формасын дәлелдеу мүмкіндігімен ерекшеленеді және
оны осы эксперименттің ықтимал нұсқаларын жалпылау үшін де пайдаланыңыз.
Бірінші деңгейден екінші деңгейге өту процесін көрсететін стандартты емес теңдеулерді шешуге үйрету ерекшеліктерін қарастырыңыз.
Эмпирикалық деңгейге жету үшін оқушылардың бұрын өткен теңдеулерді шешу үшін айнымалының өзгеруін қолданумен байланысты «жинақталған» Бұл кезеңнің негізгі мақсаты – дағдыларды қатаң түрде қалыптастыру
зерттелетін теңдеудегі тригонометриялық ауыстыру қажеттілігін негіздеу үшін функцияның параметрлік графигін құрудың дұрыстығын ғана емес, сонымен қатар (-1; 1) аралықта орналасқан түбірлер санының динамикалық тұрақтылығын дәлелдеу. берілген параметр -1 <ɑ<1. Осыған орай, бұл деңгейдегі әдістеменің негізіне математиканы оқытудағы танымдық-бейнелік көзқарас болуы керек, оны В.А. Далингер [7].
Осы көзқарас тұрғысынан сол жағының функциясының графигі берілген
теңдеулер алгебралық операцияларды көрнекі қолдау құралы ретінде әрекет етеді,
х осімен қиылысу нүктелерінің саны мен орналасуының эмпирикалық анықталған фактісін түсіндіру барысында орындалады. Ұсынылған әрбір кезеңдегі стандартты емес теңдеумен жұмыс істеудің өзгеруі жаңа операциялардың пайда болуымен көрінеді: функция графигін салу және оны негіздеу; алынған нәтижелердің алгебралық дәлелі. Осы операцияларды қолдану ерекшеліктерін алдыңғы теңдеудің шешімін жобалау мысалында қарастырыңыз, оны бұрын оны келесі түрде қайта жазыңыз:тәжірибесін жүйелеу қажет.
Мсыал-2: 4x3 3x a 0
Осы теңдеумен жұмысты абстрактілі-теориялық деңгейде CKA GeoGebra көмегімен толық көрсету үшін бос терминді параметрлеу және тапсырма шарттарын шешуден дәлелдеуге өзгерту қажет.
y 4x3 3x
1. Функцияның графигін салыңыз
Төменгі панельдің «INPUT» терезесінде деректерді сызықтық түрде жазамыз, содан кейін «SLIDER» бөлімінде -1-ден 1-ге дейін параметр мәнінің қажетті интервалын орнатамыз .
2. Компьютерлік эксперимент жүргіземіз.
Тәжірибенің мақсаты -1<а<1 параметрін өзгерту кезінде абсцисса осімен қиылысу нүктелерінің санын тексеру (яғни, теңдеудің түбірлерінің санын анықтау және олардың сандық бағасы).
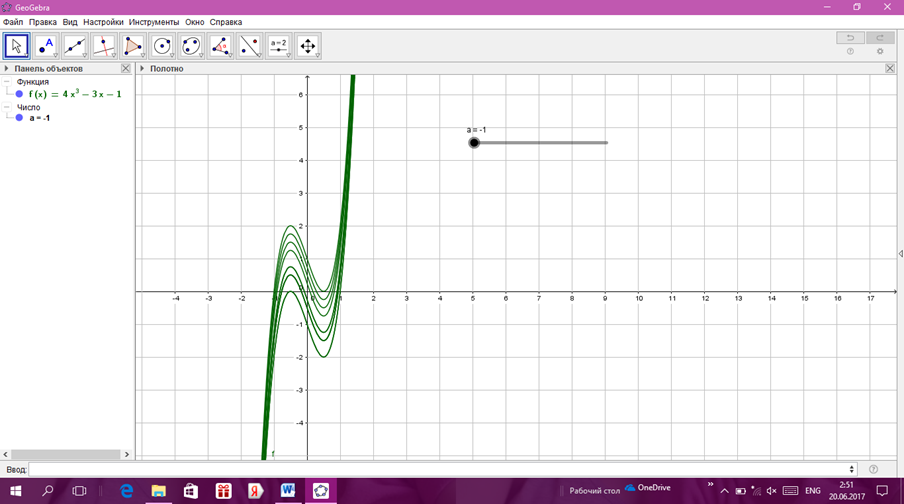
Эксперимент барысы:
a) параметрінің мәні -1-ден 1-ге дейін өзгеретіндей етіп, SLIDER құралын алдын ала белгіленген қадаммен жылжытыңыз (көзбен қабылдаудың ыңғайлылығы үшін параметр қадамының ұсынылатын өзгерісі 0,25).
б) х осімен қиылысу нүктелерінің санын және олардың сандық мәнін байқаймыз. Олардың саны өзгеріссіз қалады, ал түбірлердің мәндері бүкіл эксперимент кезінде модуль 1-ден аспайды.
Қорытынды: эксперимент параметрдің берілген мәні үшін екенін растады
бастапқы теңдеудің абсолютті мәні бойынша әрқайсысы 1-ден кем болатын дәл үш түрлі түбірі бар.
Әдебиет:
Грейв, Д.А. Бастауыш алгебраны оқыту туралы / Д.А.Грав. - Б.: К.Л.Рикер баспасы, 1915. - 27 б. Гусев, В.А.
Математиканы оқытудың психологиялық-педагогикалық негіздері / В.А.Гусев. — М.: Verbum-M: Ред. Орталық «Академия», 2003. – 432 б. Ермаков, В.П.
Алгебраны бастапқы оқыту туралы / В.П. Ермаков // Эксперименттік физика және элементар математика хабаршысы. — [Киев]: тип-литография. жолдас I. N. Кушнерев және, 1890. - Шығарылым. № 102. — С. 2–8. Лексин, Н. Г. Алгебра әдістері / Н. Г. Лексин. – Қазан, 1916. – 346 б. Нечаев, Н.В.
Алгебраны бастапқы оқыту туралы / Н.В.Нечаев. - Санкт-Петербург: Баспахана. М.М.: Стасюлевич, 1892. - 32 б. Розенберг, В.Л.
Арифметикадан алгебраға қарапайым көшу / В.Л. Розенберг. – Петербург, 1914. – 35 б.1>