ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 11
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» |
| Кафедра экономики и управления Форма обучения: очно-заочная |
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
Математика
Группа Ал22Э161в
Студент
Орынбаев Азиз
МОСКВА 2023
Задания для практических занятий.
Задачи:
-
Методом изоклин построить интегральные кривые уравнения
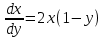
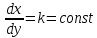
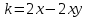
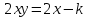
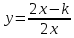
Построим интегральную кривую:
При
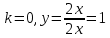
При
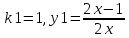
При
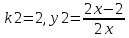
При
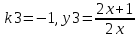
При
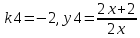
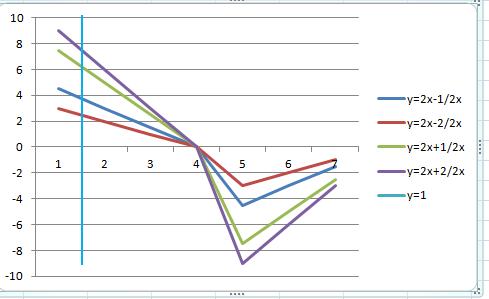
2. Решить уравнение, допускающее понижение порядка
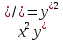
Это дифференциальное уравнение имеет вид:
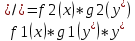
где
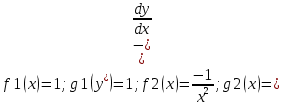
Приведем уравнение к виду:
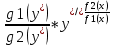
Разделим обе части уравнения на
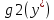
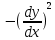
Получим
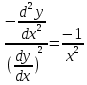
Этим самым мы разделим переменные
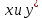
Теперь помножим обе части уравнения на
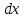, тогда уравнение будет таким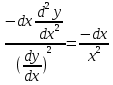
или
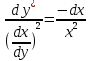
Возьмем от обеих частей уравнения интегралы
от левой части интеграл по
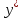
от правой части интеграл по
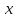
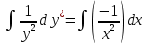
Возьмем эти интегралы
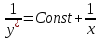
Мы получили уравнение с неизвестной
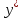
Решение будет такое:
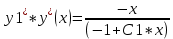
Возьмем эти интегралы
-
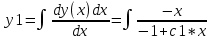
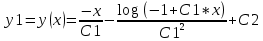
Решить систему уравнений
-
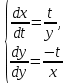
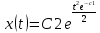
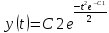
Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10.
Даны m=10, p=0,7. Необходимо найти n.
Используем формулу:
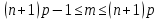
Подставим данные в формулу:
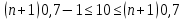
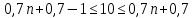
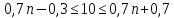
Получим систему неравенств:
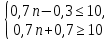
Из первого неравенства получим:
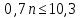
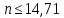
Из второго неравенства получим:
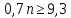
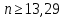
Получим n в виде:
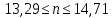
n=14
Таким образом, при наивероятнейшем числе появлений события равным 10 (m) и вероятности появления события в каждом испытании равной 0,7 (p) будет проведено 14 испытаний (n).