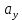ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 30
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образование
«Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых»
(ВлГУ)
Кафедра архитектуры
ПРАКТИЧЕСКАЯ РАБОТА №2
по дисциплине
«Разделы математики»
на тему:
«ВЕКТОРНАЯ АЛГЕБРА»
Выполнил:
ст. гр. АРХ-222
Новичихина А. А.
Принял:
доцент каф. ФАиП
Кондакова Е.Н.
Владимир 2023 г.
ЦЕЛЬ РАБОТЫ: усвоить теоретический материал и применить его на практике.
ЗАДАНИЕ:
1. Усвоить теоретический материал по темам: «Векторы и операции над ними».
2. Выполнить и записать решение 3 задач (вариант соответствует номеру в списке группы) в тетрадь для практических работ.
3. Выполнить проверку найденных решений с помощью online-сервисов:
- https://ru.onlinemschool.com/math/.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ:
Вектор - это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление.
Если А - начало вектора, а В - его конец, то вектор обозначается символом
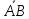или а. Вектор 
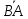(у него начало в точке В, а конец в точке А) называется противоположным вектору 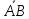. Вектор, противоположный вектору 
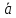, обозначается - 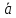.Длиной или модулем вектора
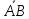называется длина отрезка и обозначается 
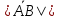. Вектор, длина которого равна нулю
, называется нулевым вектором и обозначается
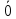. Нулевой вектор направления не имеет.Вектор, длина которого равна единице, называется единичным вектором и обозначается через
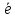. Единичный вектор, направление которого совпадает с направлением вектора 
, называется ортом вектора и обозначается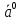 
.Векторы
и 
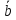называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают || 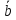.Коллинеарные векторы могут быть направлены одинаково или противоположно.
Нулевой вектор считается коллинеарным любому вектору.
Два вектора
и 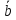называются равными ( = 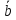), если они коллинеарны, одинаково направлены и имеют одинаковые длины.Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространства.
Равные векторы называют также свободными.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.
Линейные операции над векторами
К линейным операциям относятся сложение, вычитание векторов, умножение вектора на число.
Пусть
и 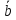- два произвольных вектора. Возьмем произвольную точку 0 и построим вектор
= . От точки А отложим вектор 
. = 
. Вектор 
, соединяющий начало первого вектора с концом второго, называется суммой векторов и : ОВ = + .Это правило сложения векторов называют правилом треугольника.
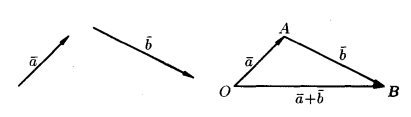
Сумму двух векторов можно построить также по правилу параллелограмма.
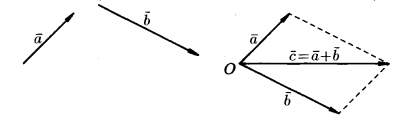
Под разностью векторов
и понимается вектор 
= 
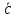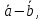такой, что + = 
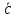Можно вычитать векторы по правилу:
- = + (- ), т. е. вычитание векторов заменить сложением вектора с вектором, противоположным вектору .Произведением вектора
на скаляр (число) 
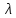
называется вектор
- т (или ã • ), который имеет длину 
• 
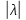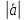, коллинеарен вектору ã, имеет направление вектора а, если > 0 и противоположное направление, если < 0. Из определения произведения вектора на число следуют свойства этого произведения:
-
если = • , то || . Наоборот, если || , ( + 0), то при некотором верно равенство = 
; -
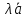всегда = •
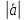, т. е. каждый вектор равен произведению его модуля на орт.
Линейные операции нал векторами обладают следующими свойствами:
1.
+ = + ,2. (
+ ) +
= + (
+
),3.
• (
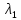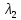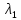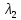• ) = • • 4. (
+
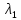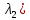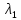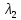• = • + • 5.
• ( + ) = • + • Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.
= 
• 
+ 
• 
+ 
•
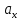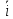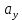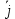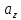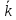
Это формула является основной в векторным исчислении и называется разложением вектора по ортам координатных осей.
,
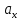