МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ
Федеральное государственное бюджетное образовательное

учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)


КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Математическая логика и теория алгоритмов»

вариант 8.


Студент гр. з-432П5-2

В. Н. Ветютнев

Направления подготовки

09.03.01

«29» марта 2023 г.

Руководитель:

Ассистент каф. АСУ,

Старший преподаватель каф. АФУ

А. В. Елецкая

« » 20 г.

Задание 1. Следующее утверждение докажите или опровергните (опровергнуть можно на частном примере): A ∈ B и B ∈ C ⇒ A ∈ C
Решение:

Пусть множество А = {1},

A ∈ B, B = {A} = {{1}};

B ∈ C, C = {B} = {{A}};

Следовательно, элементом множества C является множество B

Ответ:

Утверждение A ∈ B и B ∈ C ⇒ A ∈ C не верно.

Задание 2. Является ли тавтологией формула

?
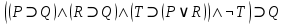Решение:

((P ⊃ Q) & (R ⊃ Q) & (T ⊃ (P ∨ R)) & ¬T) = И	Q = Л
(P ⊃ Q) & (R ⊃ Q) & (T ⊃ (P ∨ R) = И, ¬T = И
(P ⊃ Л) & (R ⊃ Л) & (T ⊃ (P ∨ R) = И, Т = Л
(P ⊃ Л) = И, (R ⊃ Л) = И, (Л ⊃ (P ∨ R)) = И
Р = Л, R = Л, (Л ⊃ (Л ∨ Л)) = И
Л ⊃ Л = И

Ответ_:_∃x∃y(Z(x)__L(y)__¬R(x,_y))_или_∃x∀y((Z(x)__L(y))_⊃_¬R(x,_y))Задание__4'>Ответ_:_В_выражении_Л_⊃_Л_=_И_нет_противоречий,_следовательно,_исходная_формула_((P_⊃_Q)__(R_⊃_Q)__(T_⊃_(P_∨_R))__¬T)_⊃_Q_не_является_тавтологией.Задание_3'>Ответ:

В выражении Л ⊃ Л = И нет противоречий, следовательно, исходная формула ((P ⊃ Q) & (R ⊃ Q) & (T ⊃ (P ∨ R)) & ¬T) ⊃ Q? не является тавтологией.

Задание 3. Переведите с естественного языка на язык логики предикатов:

Зайцы не всегда глупее лис.

---

Решение.

Универсум:

M = {животные}.

Предикаты:

Z (x) ≡ «x - заяц»,

L (x) ≡ «x - лиса»,

R (x, y) ≡ «x - глупее y».

Существует хотя бы один заяц, который не глупее хотя бы одной лисы.

∃x∃y(Z(x) & L(y) & ¬R(x, y))

Существует хотя бы один заяц, который не глупее всех лис.

∃x∀y((Z(x) & L(y)) ⊃ ¬R(x, y))
Ответ:

∃x∃y(Z(x) & L(y) & ¬R(x, y)) или ∃x∀y((Z(x) & L(y)) ⊃ ¬R(x, y))

Задание 4. Переведите с естественного языка на язык логики предикатов:

Все честные ученые уважают друг друга.
Решение:

Универсум:

M = {ученые}.

Пусть предикаты:

S(x) ≡ «x – честный учёный»,

R(x, y) ≡ «x уважает y»

Тогда формула будет иметь вид:


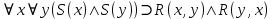
Ответ:


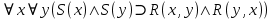
Задание 5. Для бинарного отношения x ρ y ⇔ «y = |x|», определенного на множестве вещественных чисел, выясните, какими свойствами оно обладает (рефлексивность, симметричность, антисимметричность, транзитивность) и какими не обладает.
Решение:

a) Данное отношение не рефлексивно.

Например, возьмем x=-2. Для него не выполняется -2=|-2|

б) Данное отношение не симметрично.

Например, возьмем x=-2 и y=2. Для такой пары y=|x| выполняется, а x=|y| не выполняется.

в) Данное отношение антисимметрично.

Пусть y=|x| и x=|y|. В таком случае оба числа неотрицательны и равны по модулю. Следовательно, они равны.

г) Данное отношение транзитивно. Пусть y=|x| и z=|y|. Тогда, z=|y|=|(|x|)|=|x|
Ответ:

Отношение антисимметрично и транзитивно.

Задание 6. Докажите, что композиция инъективных отображений есть инъективное отображение.
Решение:

Пусть даны два отображения 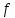и 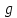. Композиция их - .

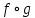Если отображение инъективно, то разные его элементы переходят в разные элементы. То есть, для 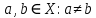следует, что 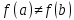. Для второго отображения аналогично .

---

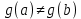1. Возьмем два элемента первого множества 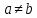. Результаты первого отображения обозначим 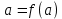и 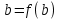. Так как отображение по условию - инъективное, то .

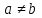2. Выполним второе отображение. Обозначим 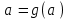и .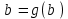

Так как второе отображение тоже инъективное, а из пункта один 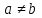, то отсюда, .

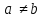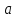3. Таким образом, композиция отображений переводит разные элементы и 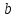в разные элементы 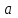и 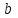, то есть является инъективным отображением.

Задание 7. Используя математическую индукцию, докажите, что


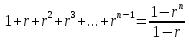
Решение:

Проверка при n=1.

,

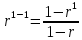тогда,

,

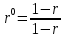следовательно, 1=1

Проверка при

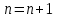
Левая часть уравнения примет вид:



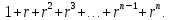
Выполним тождественные преобразования.



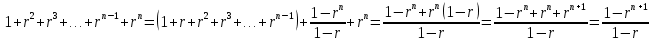
Следовательно, при n = n + 1



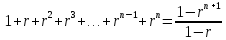
Что и требовалось доказать.

Задание 8. Расположите следующие 5 функций в порядке увеличения скорости роста (каждая функция есть O (следующая)):


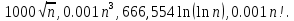
Решение:

Функция 666 на всей области значений постоянна, следовательно, её увеличение скорости роста = 0. Значит, данная функция будет расположена на первом месте в порядке увеличения скорости.

---

Существуют правила оценки скорости роста функций. Применим их к данным функциям.

1) Постоянные множители можно опускать.

Тогда исходные функции можно заменить следующими:



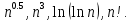
2) Используя правило, гласящее, что любой полином растет быстрее любого логарифма, а также принимая в учёт тот факт, что скорость роста факториала переменной растёт значительно быстрее (приблизительно при значениях >= 6), чем куб переменной, то расположим формулы в порядке увеличения скорости роста:



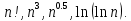
Тогда вернув функции в исходное состояние, расположим их в порядке увеличения скорости роста.

Итак, сначала идет невозрастающая функция, затем логарифмическая, далее степенная степени 0,5, далее степенная степени 3, далее факториальная функция.
Ответ:

---

Смотрите также файлы

• Контрольная работа по дисциплине Сейсмостойкость зданий и сооружений Вариант 7 Выполнил студент группы.docx

• Практикум Дисциплина Практика оценки стоимости недвижимости.docx

• 1) мотив, цель и эмоции (понятие и значение) Мотив преступления.docx

• Практическая работа к теме 6 Человек созидание Тема занятия День российской науки Класс 7.docx

• Лекция Этические нормы и принципы в работе психолога.doc