Файл: Учебника иностранного языка дисциплина Учебная практика, практика по применению математической статистики в исследованиях.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 77
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
по характеру связи является прямой.
Так как 0,3 rX1, X 2 0,7 , то связь между распределением по силе связи является средней.
Вывод: существует прямая связь между обьемом текстов и этапом обучения, но данная связи средняя по силе.
ЧАСТЬ 3.2
Осуществим ранжирование количества слов в текстах УМК 1 и 2, записанных в виде таблицы от максимума к минимуму:
Для вычисления ранга нужно найти среднее значение из показателей места. В нашем случае, одинаковое значение 21 показателя Х отражено в 1 и 2 месте, что дает нам 1+2/2=1.5, значение 20 отражено в 3 и4 месте, т.о 3+4/2=3,5 и т.д.
Получим значение суммы квадратов разности рангов:
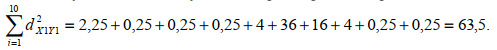
Получим значение коэффициента ранговой корреляции Спирмена:
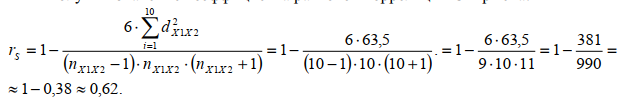
В нашем случае rS 0,62 .
Критические значения коэффициента корреляции рангов Спирмена при n = 10 равны 0,64 (p = 0,05) и 0,79 (p = 0,01).
При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 - признаком слабой тесноты связи; значения более 0,3, но менее 0,7 - признаком умеренной тесноты связи, а значения 0,7 и более - признаком высокой тесноты связи.
Также для оценки тесноты связи может использоваться шкала Чеддока:
Вывод: между объёмом текстов для чтения и этапом обучения существует средняя корреляционная связь.
ЧАСТЬ 3.3
Групповая работа: доказательство или опровержение НОВОЙ гипотезы.
Осуществим ранжирование времени звучания в текстах УМК 1 и 2, записанных в виде таблицы от максимума к минимуму:
Для вычисления ранга нужно найти среднее значение из показателей места. В нашем случае, одинаковое значение 2 показателя Х отражено в 1 и 2 месте, что дает нам 1+2/2=1.5, значение 1,5 отражено в 3 и4 месте, т.о 3+4/2=3,5 и т.д.
Получим значение суммы квадратов разности рангов:

Получим значение коэффициента ранговой корреляции Спирмена:

В нашем случае rS 0,62 .
Критические значения коэффициента корреляции рангов Спирмена при n = 10 равны 0,64 (p = 0,05) и 0,79 (p = 0,01).
При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 - признаком слабой тесноты связи; значения более 0,3, но менее 0,7 - признаком умеренной тесноты связи, а значения 0,7 и более - признаком высокой тесноты связи.
Также для оценки тесноты связи может использоваться шкала Чеддока:
Вывод: между временем звучания аудиотекста и этапом обучения существует средняя корреляционная связь.
Так как 0,3 rX1, X 2 0,7 , то связь между распределением по силе связи является средней.
Вывод: существует прямая связь между обьемом текстов и этапом обучения, но данная связи средняя по силе.
ЧАСТЬ 3.2
Ранговый коэффициент корреляции Спирмена
Осуществим ранжирование количества слов в текстах УМК 1 и 2, записанных в виде таблицы от максимума к минимуму:
| Место | Количество слов УМК1 | Место | Количество слов УМК2 |
| 3 | 20 | 1 | 24 |
| 1 | 21 | 2 | 24 |
| 9 | 13 | 9 | 15 |
| 5 | 17 | 5 | 17 |
| 4 | 20 | 6 | 17 |
| 2 | 21 | 8 | 16 |
| 6 | 17 | 3 | 24 |
| 7 | 17 | 4 | 21 |
| 10 | 13 | 10 | 13 |
| 8 | 16 | 7 | 16 |
Для вычисления ранга нужно найти среднее значение из показателей места. В нашем случае, одинаковое значение 21 показателя Х отражено в 1 и 2 месте, что дает нам 1+2/2=1.5, значение 20 отражено в 3 и4 месте, т.о 3+4/2=3,5 и т.д.
| УМК1 (X1) | УМК2 (X2) | РангУМК1 rX1 | РангУМК 2 rX2 | Разность ранговоценок dX1X2 r(X1)r(X2) | Квадратразностирангов d2 X1X2 | ||
| Место | Ранг | Место | Ранг | ||||
| 20 | 24 | 3 | 3,5 | 1 | 2 | 3,5 −2 =1,5 | 1,5² =2,25 |
| 21 | 24 | 1 | 1,5 | 2 | 2 | 1,5 −2=−0,5 | (-0,5)²= 0,25 |
| 13 | 15 | 9 | 9,5 | 9 | 9 | 9,5 −9 =0,5 | 0,5² =0,25 |
| 17 | 17 | 5 | 6 | 5 | 5,5 | 6 −5,5 =0,5 | 0,5² =0,25 |
| 20 | 17 | 4 | 3,5 | 6 | 5,5 | 3,5 −5,5=−2 | (−2)² =4 |
| 21 | 16 | 2 | 1,5 | 8 | 7,5 | 1,5 −7,5= −6 | (-6)²= 36 |
| 17 | 24 | 6 | 6 | 3 | 2 | 6 − 2= 4 | 4² =16 |
| 17 | 21 | 7 | 6 | 4 | 4 | 6 – 4= 2 | 2² = 4 |
| 13 | 13 | 10 | 9,5 | 10 | 10 | 9,5 –10=−0,5 | (-0,5)²= 0,25 |
| 16 | 16 | 8 | 8 | 7 | 7,5 | 8 −7,5 =0,5 | 0,5² =0,25 |
| Суммы (Итого): | 55 | 55 | 55 | 55 | 0 | 63,5 | |
Получим значение суммы квадратов разности рангов:
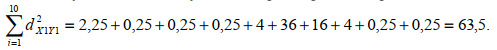
Получим значение коэффициента ранговой корреляции Спирмена:
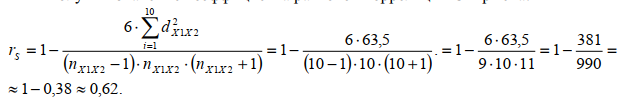
В нашем случае rS 0,62 .
Критические значения коэффициента корреляции рангов Спирмена при n = 10 равны 0,64 (p = 0,05) и 0,79 (p = 0,01).
При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 - признаком слабой тесноты связи; значения более 0,3, но менее 0,7 - признаком умеренной тесноты связи, а значения 0,7 и более - признаком высокой тесноты связи.
Также для оценки тесноты связи может использоваться шкала Чеддока:
| Абсолютное значение rxy | Теснота (сила) корреляционной связи |
| менее 0.3 | слабая |
| от 0.3 до 0.5 | умеренная |
| от 0.5 до 0.7 | заметная |
| от 0.7 до 0.9 | высокая |
| более 0.9 | весьма высокая |
Вывод: между объёмом текстов для чтения и этапом обучения существует средняя корреляционная связь.
ЧАСТЬ 3.3
Групповая работа: доказательство или опровержение НОВОЙ гипотезы.
Ранговый коэффициент корреляции Спирмена
Осуществим ранжирование времени звучания в текстах УМК 1 и 2, записанных в виде таблицы от максимума к минимуму:
| Место | Время звучания УМК1 | Место | Время звучания УМК2 |
| 3 | 1,5 | 1 | 3,5 |
| 1 | 2 | 2 | 3,5 |
| 9 | 0,8 | 9 | 2 |
| 5 | 1 | 5 | 3 |
| 4 | 1,5 | 6 | 3 |
| 2 | 2 | 8 | 2,5 |
| 6 | 1 | 3 | 3,5 |
| 7 | 1 | 4 | 3 |
| 10 | 0,5 | 10 | 1 |
| 8 | 0,8 | 7 | 2,5 |
Для вычисления ранга нужно найти среднее значение из показателей места. В нашем случае, одинаковое значение 2 показателя Х отражено в 1 и 2 месте, что дает нам 1+2/2=1.5, значение 1,5 отражено в 3 и4 месте, т.о 3+4/2=3,5 и т.д.
| УМК1 (X1) | УМК2 (X2) | Ранг УМК1 rX1 | Ранг УМК 2 rX2 | Разность рангов оценок dX1X2 r(X1)r(X2) | Квадрат разности рангов d2 X1X2 | ||
| Место | Ранг | Место | Ранг | ||||
| 1,5 | 3,5 | 3 | 3,5 | 1 | 2 | 3,5 −2 =1,5 | 1,5² =2,25 |
| 2 | 3,5 | 1 | 1,5 | 2 | 2 | 1,5 −2=−0,5 | (-0,5)²= 0,25 |
| 0,8 | 2 | 9 | 9,5 | 9 | 9 | 9,5 −9 =0,5 | 0,5² =0,25 |
| 1 | 3 | 5 | 6 | 5 | 5,5 | 6 −5,5 =0,5 | 0,5² =0,25 |
| 1,5 | 3 | 4 | 3,5 | 6 | 5,5 | 3,5 −5,5=−2 | (−2)² =4 |
| 2 | 2,5 | 2 | 1,5 | 8 | 7,5 | 1,5 −7,5= −6 | (-6)²= 36 |
| 1 | 3,5 | 6 | 6 | 3 | 2 | 6 − 2= 4 | 4² =16 |
| 1 | 3 | 7 | 6 | 4 | 4 | 6 – 4= 2 | 2² = 4 |
| 0,5 | 1 | 10 | 9,5 | 10 | 10 | 9,5 –10=−0,5 | (-0,5)²= 0,25 |
| 0,8 | 2,5 | 8 | 8 | 7 | 7,5 | 8 −7,5 =0,5 | 0,5² =0,25 |
| Суммы (Итого): | 55 | 55 | 55 | 55 | 0 | 63,5 | |
Получим значение суммы квадратов разности рангов:

Получим значение коэффициента ранговой корреляции Спирмена:

В нашем случае rS 0,62 .
Критические значения коэффициента корреляции рангов Спирмена при n = 10 равны 0,64 (p = 0,05) и 0,79 (p = 0,01).
При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 - признаком слабой тесноты связи; значения более 0,3, но менее 0,7 - признаком умеренной тесноты связи, а значения 0,7 и более - признаком высокой тесноты связи.
Также для оценки тесноты связи может использоваться шкала Чеддока:
| Абсолютное значение rxy | Теснота (сила) корреляционной связи |
| менее 0.3 | слабая |
| от 0.3 до 0.5 | умеренная |
| от 0.5 до 0.7 | заметная |
| от 0.7 до 0.9 | высокая |
| более 0.9 | весьма высокая |
Вывод: между временем звучания аудиотекста и этапом обучения существует средняя корреляционная связь.