Файл: Контрольная работа теоретиче с кие основы ин ф орматики оглавление введение.doc

Существует строгое доказательство того, что по возможностям преобразования нормальные алгоритмы Маркова эквивалентны машинам Тьюринга.Задание 4Определить теоретическую вычислительную сложность задач:  полного обхода троичного сбалансированного дерева; поиска подстроки в строке;  поиска подграфа в графе;  слияния двух упорядоченных списков в упорядоченный список;  умножения двух матриц.Решение:Использование сортированных бинарных деревьев достаточно эффективно с точки зрения временных оценок. Оценим вычислительную сложность основных операций с данной структурой.

Операция поиска вершины.

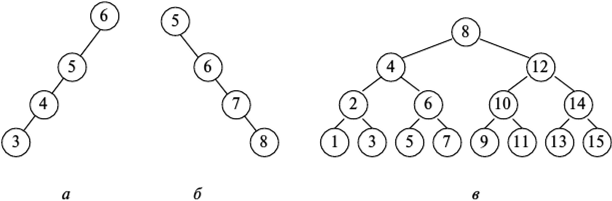
Худшим случаем при поиске вершины является случай, когда дерево имеет вид последовательности вершин (рис. 1, а, б). В этом случае для поиска вершины в среднем потребуется (и + 1)/2 проверок, как при последовательном поиске, например в массиве, или О_х (и).Рис. 1. Виды бинарных деревьев: а, б—с последовательностью вершин; в — сбалансированное деревоОценку в среднем выполним для сбалансированного дерева (рис. 7.20, в). Поиск вершины в этом случае потребует (log₂ п + + 1)/2 проверок, т.е. получаем вычислительную сложность в среднем 0_Ср (log₂ п).

Операция построения дерева.

Худшим случаем при построении дерева является дерево, представляющее собой последовательность вершин, так как при этом поиск вершины, к которой необходимо добавить новую, потребует максимального числа проверок. Количество проверок в этом случае: (п — 1) — для последнего элемента, 1 — для второго (для первого элемента проверки не требуется). В среднем необходимо [(п — 1) + 1]/2 проверок; умножив на (п — 1) элемент, получаем п{п — 1)/2 проверок, или О_х(п²).Оценку в среднем выполним также на сбалансированном дереве. Количество проверок для поиска родительской вершины составит (log₂ (я — 1) + 1)/2; соответственно, умножив на (и — 1), получим О_ср(п log₂ п).

Операция обхода дерева в процессе получения сортированной последовательности.

Для деревьев обоих видов сложность одинакова, так как для каждой вершины при обходе проверяется наличие левого и правого поддеревьев, т.е. суммарное количество проверок равно 2п. Следовательно, вычислительная сложность операции обхода равна О(п). С учетом построения дерева вычислительная сложность в среднем составит Оср (я log2 я).

---

ЗАКЛЮЧЕНИЕВ ходе выполнения контрольной работы мы закрепили полученные теоретические знания по дисциплине теоретические основы информатикиСписок рекомендуемойлитературы1. БезручкоВ.Т.Информатика(курслекций):учеб.пособие/В.Т. Безручко–М.:ИД«Форум»:ИНФРА-М,2020.–432с.Режимдоступа: https://znanium.com/bookread2.php?book=10365982. Теоретическиеосновыинформатики:учеб./Р.Ю.Царёв,А.Н. Пупков,Е.В.Самарин[идр.].–Красноярск:Сиб.федер.ун-т,2015.– 176 с.Режимдоступа: https://znanium.com/bookread2.php?book=5498013. Гуриков С.Р.Информатика:учебник/С.Р. Гуриков–М.:ФОРУМ: ИНФРА-М, 2018. – 463с. Режим доступа: https://znanium.com/bookread2.php?book=10101434. БарскийА.Б.Теорияцифровогокомпьютера[Электронныйре-сурс]:учеб.пособие/А.Б. Барский,В.В. Шилов.–М.:ИНФРА-М,2018.– 304 с. Режимдоступа:https://znanium.com/bookread2.php?book=912953

---