Файл: Отчет по курсу теория измерений голубева М. К студентка группы 3334 Преподаватель Бельский А. М.docx
Добавлен: 03.12.2023
Просмотров: 37
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 Казанский национальный исследовательский технический университет имени
Казанский национальный исследовательский технический университет имени А. Н. Туполева – КАИ
Институт автоматики и электронного приборостроения
Кафедра электронного приборостроения и менеджмента качества
ОТЧЕТ ПО КУРСУ
ТЕОРИЯ ИЗМЕРЕНИЙ
Выполнила: Голубева М.К..
студентка группы 3334
Преподаватель: Бельский А.М.
Казань 2018
1. Основы математической статистики
Математическая статистика – это раздел прикладной математики, в которой с помощью наблюдений и экспериментов стараются выяснить и сформировать законы и характеристики случайных величин. Математическая статистика, опираясь на теорию вероятности, помогает обрабатывать статистические данные во многих областях деятельности человека.
Основные задачи математической статистики:
1.Создание методов сбора и группировки данных, полученных в результате наблюдений за случайными процессами.
2. Разработка методов анализа полученных статистических данных.
3. Получение выводов по данным наблюдений
Для анализа собранных данных нам необходимо их оценить и выразить вероятность события. Также в анализ входят функции распределения вероятностей или плотности вероятностей, оценка параметров известного распределения, оценка связей между случайными величинами.
Основные понятия математической статистики – генеральная совокупность и выборка.
Генеральная совокупность – это все множество исследования объектов вида, над которыми проводятся наблюдения. Она может быть бесконечной и конечной.
Выборкой (выборочной совокупностью)называется совокупность случайно отобранных объектов из генеральной совокупности, которая необходима для исследования.
Чтобы отчетливо отражать свойства генеральной совокупности, выборка должна быть представительной или репрезентативной. Выборочная совокупность бывает повторной, когда отобранный объект возвращают в генеральную совокупность, и бесповторной, когда объект не возвращают обратно.
Существует несколько способов получения выборки:простой, типический, серийный, механический.
1) Простой отбор
– случайное извлечение объектов из генеральной совокупности с возвратом или без возврата.
2) Типический отбор, когда объекты отбираются не из всей генеральной совокупности, а из ее «типической» части.
3) Серийный отбор – объекты отбираются из генеральной совокупности не по одному, а сериями.
4)Механический отбор - генеральная совокупность «механически» делится на столько частей, сколько объектов должно войти в выборку и из каждой части выбирается один объект.
Для обработки данных наблюдаемые значения случайной величины располагают в порядке возрастания, то есть используют операциюранжирования:
1.Размах варьирования R=
2.Мода (
3.Медиана (
Когда изучаемая случайная величина Х является непрерывной или число значений её велико, то составляют интервальный статистический ряд.
Эмпирической функцией (функцией распределения выборки) называется функция F*(x), определяющая для каждого значения х частость события
где n – число выборки , nx – число наблюдений, меньших x
Эмпирическая функция F*(х) является оценкой интегральной функции F(x) в теории вероятностей.
Функция F*(х) обладает теми же свойствами, что и функция F(x):
1.
2. F*(x) – неубывающая функция
3.
Для интегральной функции распределения F(x):
Чтобы изобразить статистическое распределение графически, используют полигона и гистограммы.
Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами (хi;ni).
Полигон служит для изображения дискретного статистического ряда. Полигон частостей является аналогом многоугольника распределения дискретной случайной величины в теории вероятностей.
Гистограммой частот (частостей) называют ступенчатую фигуру, состоящую из прямоугольников, основания которых расположены на оси Ох и длины их равны длинам частичных интервалов (h), а высоты равны отношению:
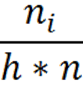 - для гистограммы
- для гистограммычастостей.
Гистограмма является графическим изображением интервального ряда. Площадь гистограммы частот равна n, а гистограммы частостей равна 1.
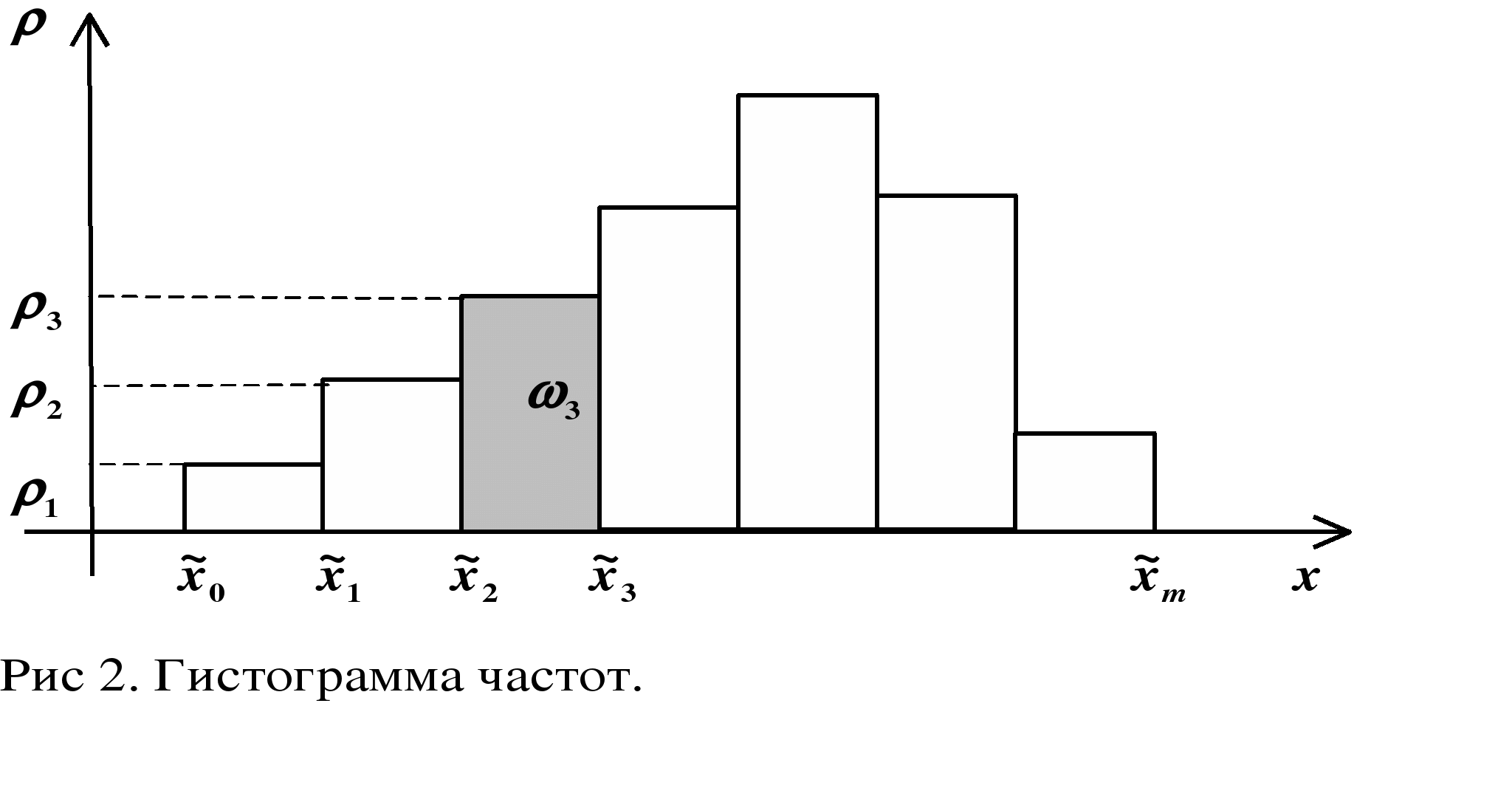
Можно построить полигон для интервального ряда, если преобразовать его в дискретный ряд. В этом случае интервалы заменяют их серединными значениями и ставят в соответствие интервальные частоты (частости).
2. Однократные измерения
Однократные измерения – совокупность операций, при которых необходимо воспроизвести единицу физической величины, сравнить с ней измеряемое значение, зафиксировать результаты сравнения и оценить погрешность измерения.
Однократные измерения можно считать частным случаем многократных измерений, потому что:
1) При совершении однократных измерений применяются средства измерений с метрологическими характеристиками, определенными при совершении многократных измерений;
2) Представление результатов измерений требует учета всех погрешностей и доверительной вероятности.
Однократные измерения требуют меньше времени, являются менее трудоемкими и более удобными для практического использования. Например, при совершении торговых операций. Необходимо отметить, что однократные измерения не проще многократных, несмотря на меньшее количество измерений и отсутствие применений вероятностных статистических методов при обработке данных.
Когда проводят однократное измерение, за результат принимают полученное значение величины. Из-за того, что по одному измерению невозможно определить погрешность результата, нужно использовать информацию, которую мы получаем априори: важно правильно выбрать средство измерений для данных условий и определить диапазоны измерений. Например, если мы собираемся измерять массу каких-либо веществ, необходимо познакомиться с весоизмерительным оборудованием и провести предварительный анализ источников погрешностей.
Правильность оценивания погрешностей результата измерений зависит от полноты учета всех факторов, влияющих на результат измерений, и от метода нахождения этих погрешностей. Конечно, в реальной жизни мы не можем учесть все возможные факторы, но всегда требуется дать наиболее точный результат.
На совершение однократных измерений существует свой нормативный документ Госстандарта России – МИ 1552-86 «Государственная система обеспечения единства измерений. Измерения прямые однократные. Оценивание погрешностей результатов измерений». МИ 1552-86 распространяется на нормативную, конструкторскую, технологическую и другую документацию, регламентирующую требования к выполнению измерений, и устанавливает методы оценивания погрешностей результатов прямых однократных измерений.
Измерения проводятся при нормальных условиях (температуры, давления и т.д.). Дополнительные погрешности, зависящие от условий измерения, в этом случае равны нулю. При расширении диапазона измерений или при условиях измерений, отличающихся от нормальных, появляются дополнительные погрешности, которые приходится учитывать.
3. Многократные наблюдения
Если необходима большая уверенность в получаемом результате, то проводятся многократные измерения. Если говорить коротко, то измеряют величину одного и того же размера, результат которого состоит из множества однократных измерений. Все проходит в одинаковых условиях с одними и теми же средствами измерения. Прежде чем приступить к обобщению результатов измерений, определяют, нет ли в полученных результатах грубых погрешностей.
За результат многократного измерения обычно принимают среднее арифметическое значение из результатов однократных измерений, входящих в ряд. Такие измерения характерны при выполнении метрологических работ, а также находят широкое применение в научных исследованиях. Важной чертой многократных измерений является получение и использование большого объема измерительной информации.
Применение многократных измерений позволяет повысить точность измерения до определенного предела, но недостаток полученной информации не позволяет получить точное значение поправок, значений составляющих погрешностей и т.п. В связи с этим устанавливают необходимое число измерений, которое позволяет получить результат измерений, в котором случайная погрешность пренебрежимо мала по сравнению с неисключенной систематической погрешностью.
Лабораторная работа №1
Оценка результатов прямых равноточных многократных измерений
Согласно ГОСТ 8.207-76 обработка результатов наблюдений производится в последовательности:
1. Исключаются известные систематические погрешности из результатов наблюдений.
2. Определяют границы неисключенной систематической погрешности (остатка) результата измерений.
3. Вычисляется среднее арифметическое исправленных результатов наблюдений, которое принимается за результат измерения.
-
Вычисляется оценка СКО результатов наблюдений.
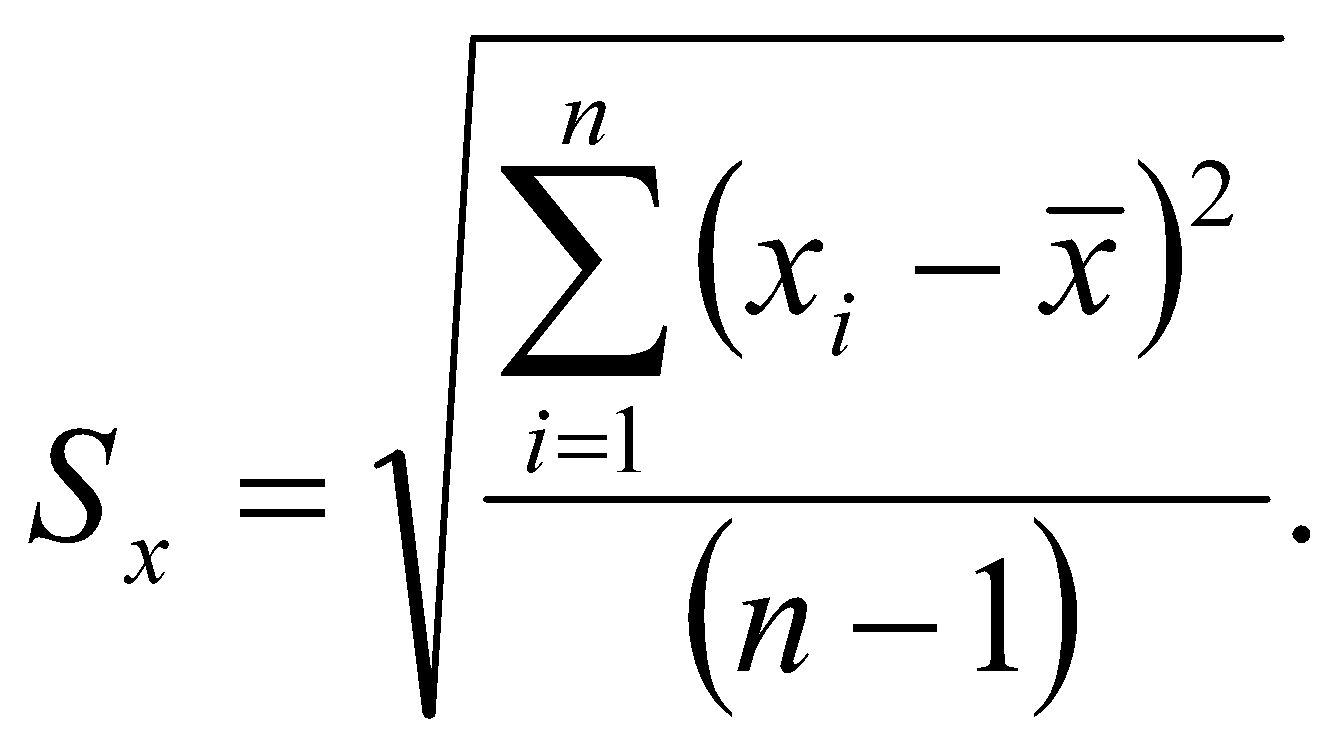
-
Проверяется наличие в группе наблюдений грубых погрешностей. Если они есть, то их исключают из группы и вновь повторяют вычисление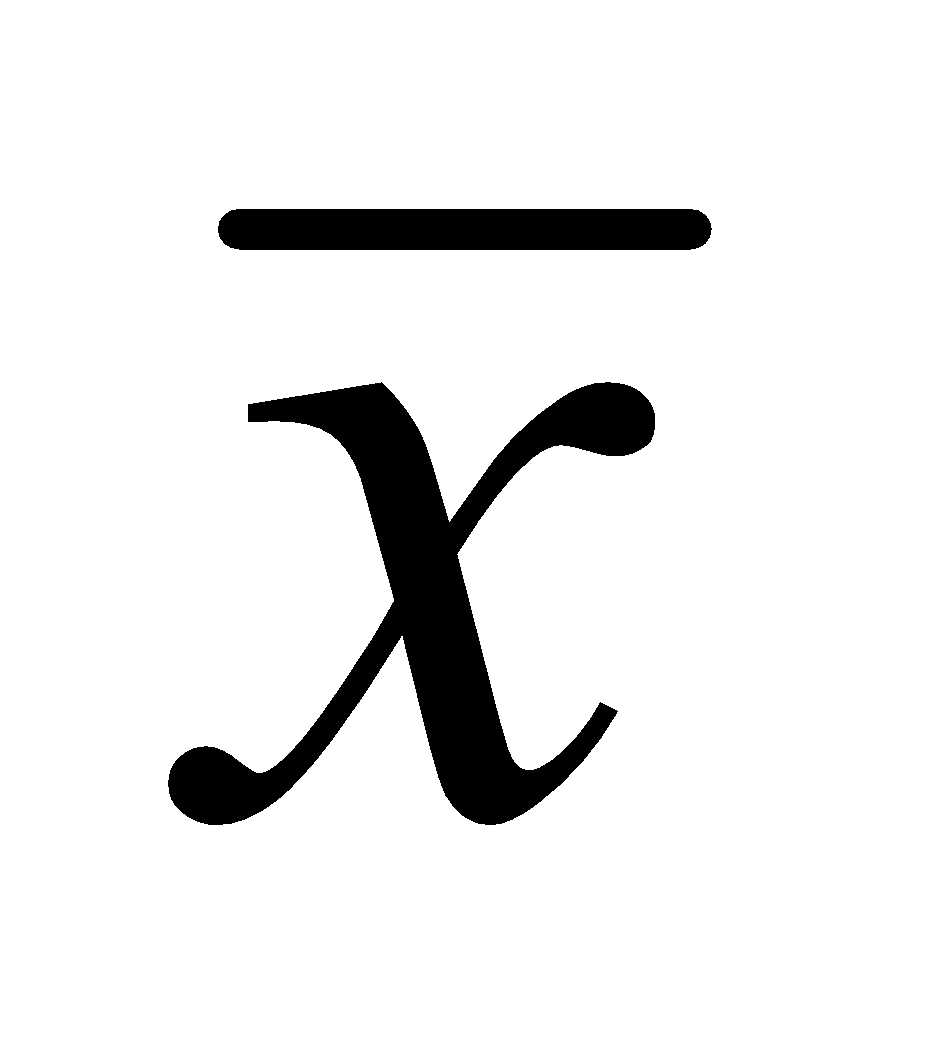 и
и 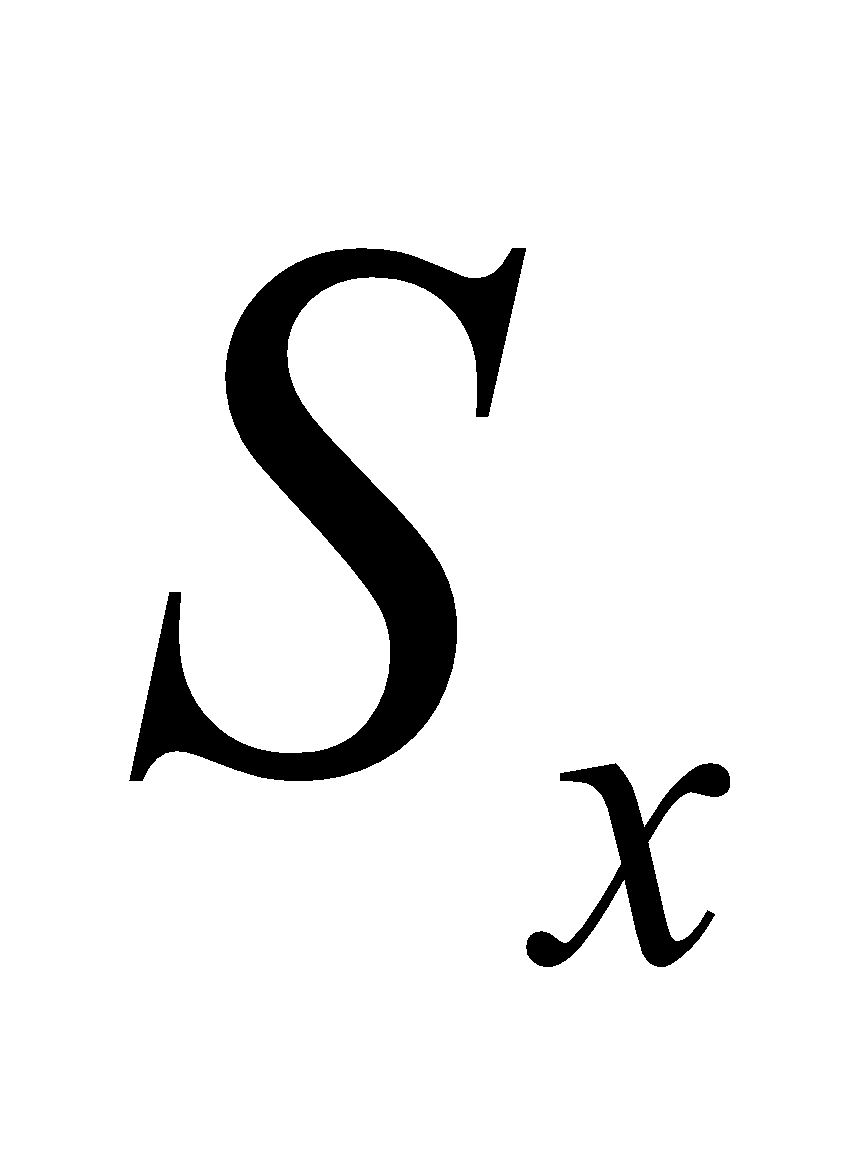 .
.
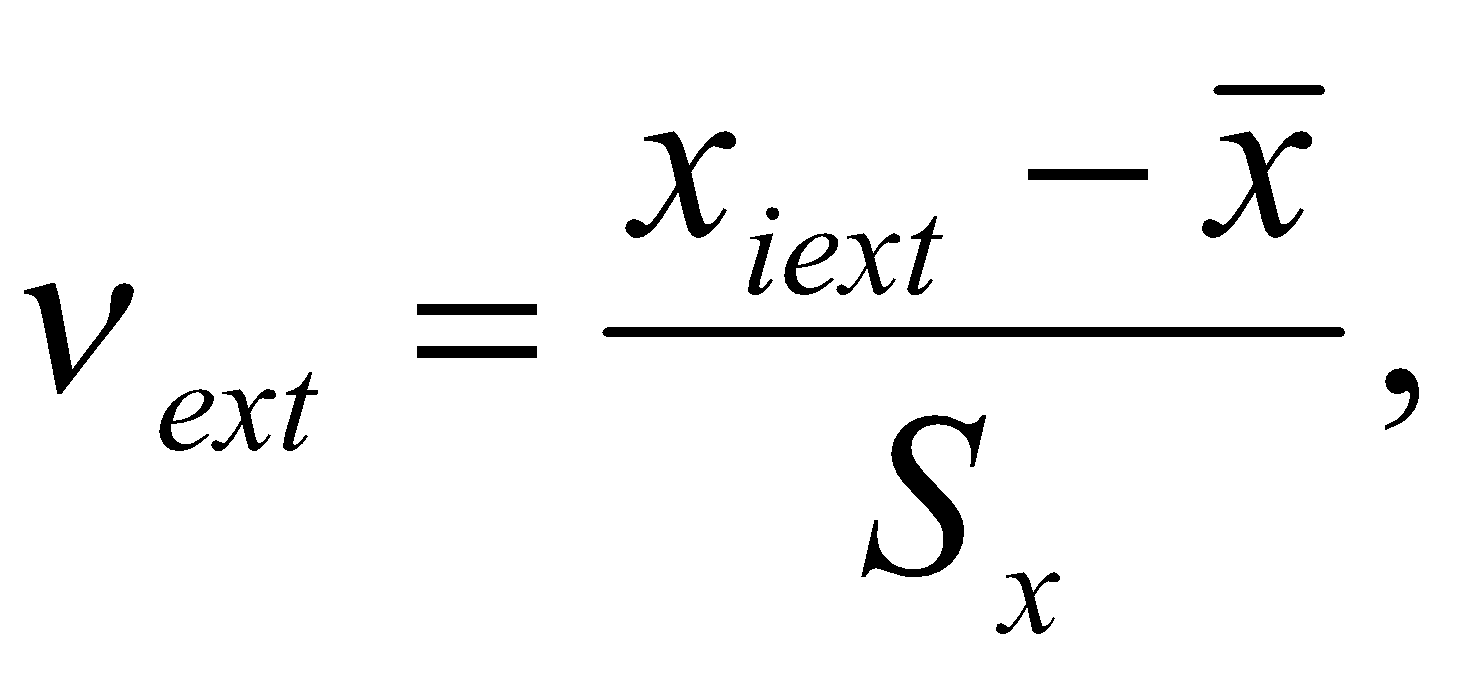
где
Полученные результаты νext сравним с приложением 1.
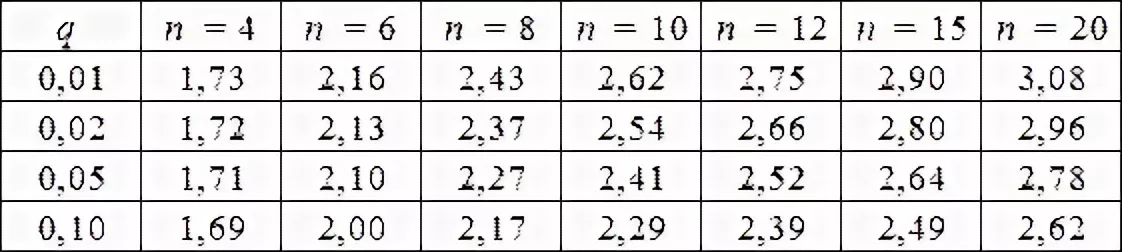
6. Вычисляют оценку СКО среднего арифметического.
7. Проверяют гипотезу о принадлежности результатов наблюдений к нормальному закону распределения.