Проверку нормальности, согласно ГОСТ 11.006–74, при n >50, проводят по критериям Пирсона или Мизеса–Смирнова.

При 15 < n < 50 используют двойной составной q–критерий.

8. Вычисляют доверительные границы случайной погрешности(случайной составляющей погрешности).

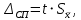
где t - коэффициент Стьюдента.

9. Вычисляют доверительные границы погрешностей результата измере-ния.

Доверительную вероятность 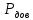принимают такой же, что при вычислении границ .
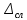Результаты измерений:

0,43

0,59

0,57

0,46

0,37

0,46

0,45

0,66

0,92

1,15

Систематические погрешности – 0,92 и 1,15.

n = 8, 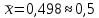, , 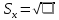Δ_сп = 3,71*0,097 = 0,36 (P_дов = 0,99, t = 3,71).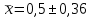



Лабораторная работа№2

Определение класса точности осциллографа

Класс точности – обобщенная характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений.

Имеется два подхода к нормированию погрешностей средств измерений.

1.Единые правила установления пределов допускаемых погрешностей показаний по классам точности регламентирует ГОСТ 8.401-80. Под классом точности СИ понимают их обобщенные характеристики, определяемые пределами допускаемой основной и дополнительной погрешности. При этом нет деления на погрешность систематическую и случайную. ГОСТ 8.401-80 не устанавливает классы точности СИ, для которых предусмотрены нормы отдельно для систематической и случайной составляющих погрешностей, а так же если необходимо их учитывать динамические характеристики. Классы точности устанавливаются в тех случаях

---

, когда погрешности СИ могут быть выражены числом или сравнительно простой формулой.

Второй метод сформулирован ГОСТ 8.009-84. “ Нормирование и использование метрологических характеристик средств измерений” Данный стандарт устанавливает комплекс метрологических характеристик, которые должны быть известны при выпуске СИ.



Результаты измерений:

3

2,9

2,9

2,9

3

3

3

3

3

3

n = 8, 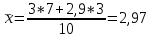, , Δ_сп = 3,3*0,48 = 0,159.

Δ =

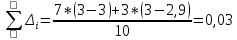
K =

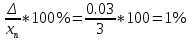
Выполнив вычисления можно сделать, что осциллограф относится к 6 классу точности..




4. Косвенные измерения

Косвенными называют такие измерения, при которых числовое значение измеряемой величины определяется по известной функциональной зависимости через другие величины, которые можно прямо измерить. При косвенных измерениях числовое значение измеряемой величины получают с участием оператора на основе прямых измерений – решением одного уравнения. К косвенным измерениям прибегают в тех случаях, когда неудобно или невозможно осуществить автоматическое вычисление известной зависимости между одной или несколькими входными величинами и измеряемой величиной. Например, мощность в цепях постоянного тока определяет оператор, умножая напряжение на ток, измеренные прямым измерением с помощью амперметра и вольтметра.

В этом случае искомое значение величины находят на основе измерения других величин в соответствии с зависимостью

Результат находят из решения уравнения, выражающего эту зависимость:

Q = f(X, Y, Z, ... , W). где Q – измеряемая величина; X, Y, Z,..., W – величины, размер которых определяется из прямых измерений.
Например, требуется измерить удельное электрическое сопротивление некоторого материала. Так как приборов для прямых измерений удельного сопротивления нет, его можно измерить только косвенно. Для этого воспользуемся уравнением

---

где р – удельное сопротивление; R – электрическое сопротивление; S – площадь поперечного сечения; L – длина образца.

Если измерить длину L, площадь поперечного сечения S и электрическое сопротивление R, то можно вычислить и его удельное сопротивление.

Косвенные измерения достаточно часто встречаются в метрологии, где ими пользуются при воспроизведении единиц. Такие измерения позволяют получать более точный результат, чем прямые. Особенно велика роль косвенных измерений в естественных науках, когда реализация прямых измерений при изучении явлений затруднительна. Например, явления, изучаемые в астрономии, молекулярной и атомной физике и т. д.

Примеры косвенных измерений: определение эффективной мощ­ности двигателя при его испытании на основании прямых измерений крутящего момента и частоты вращения вала двигателя; определе­ние площади фигур или объема тел по прямым измерениям их гео­метрических размеров.

Методика обработки результатов косвенных измерений приведена в МИ2083-90 «ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей».

Совместные и совокупные измерения

Эти измерения характеризуются тем, что значения искомых величин находят из решения системы уравнений, которые связывают искомые величины с некоторыми другими, получаемыми в результате эксперимента посредством прямых или косвенных измерений.

Если измеряемые величины - одноименные, измерения называются совокупными, если неодноименные – совместными.

Целью таких измерений обычно является установление функциональной зависимости между измеряемыми величинами. Это возможно путем замены экспериментальных данных значениями некоторой теоретической функции. Если замена справедлива для всех значений аргумента в заданном интервале, то заменяющую функцию называют аппроксимирующей. Если замена справедлива только для некоторых, дискретных значений аргумента –функцию называют интерполирующей.

Очевидно, что подобные задачи должны решаться в два этапа:

∙ выбор структуры предполагаемой зависимости, т. е. выбор вида математической модели (линейная, полиномиальная, экспоненциальная и т. п.);

∙ вычисление параметров (коэффициентов) этой модели.

В связи с этим, при выполнении совместных измерений, во-первых, возникает задача выбора аппроксимирующее зависимости

---

так, чтобы она наилучшим образом описывала истинную зависимость, во-вторых, необходимо ответить на вопрос – действительно ли выбранная функция наилучшим образом приближается к искомой зависимости и какой мерой можно оценить близость экспериментальной зависимости к истинной.

Одним из возможных вариантов решения подобных задач это применение метода наименьших квадратов (МНК).

В этом методе оценки параметров выбранной модели определяют из условия, что сумма квадратов отклонений расчетных значений аппроксимирующей функции от экспериментальных значений должна быть минимальна. При этом полагают, что результаты измерений удовлетворяет условиям:

∙ значения аргументов известны точно;

∙ систематические погрешности из исключены, а результаты измерений содержат только случайные составляющие погрешности, которые независимы, имеют одинаковые дисперсии и распределены по нормальному закону.

При выполнении этих условий МНК дает несмещенные оценки параметров модели, имеющие минимальные дисперсии.

Пусть искомые значения величин находятся из решения системы линейных уравнений:

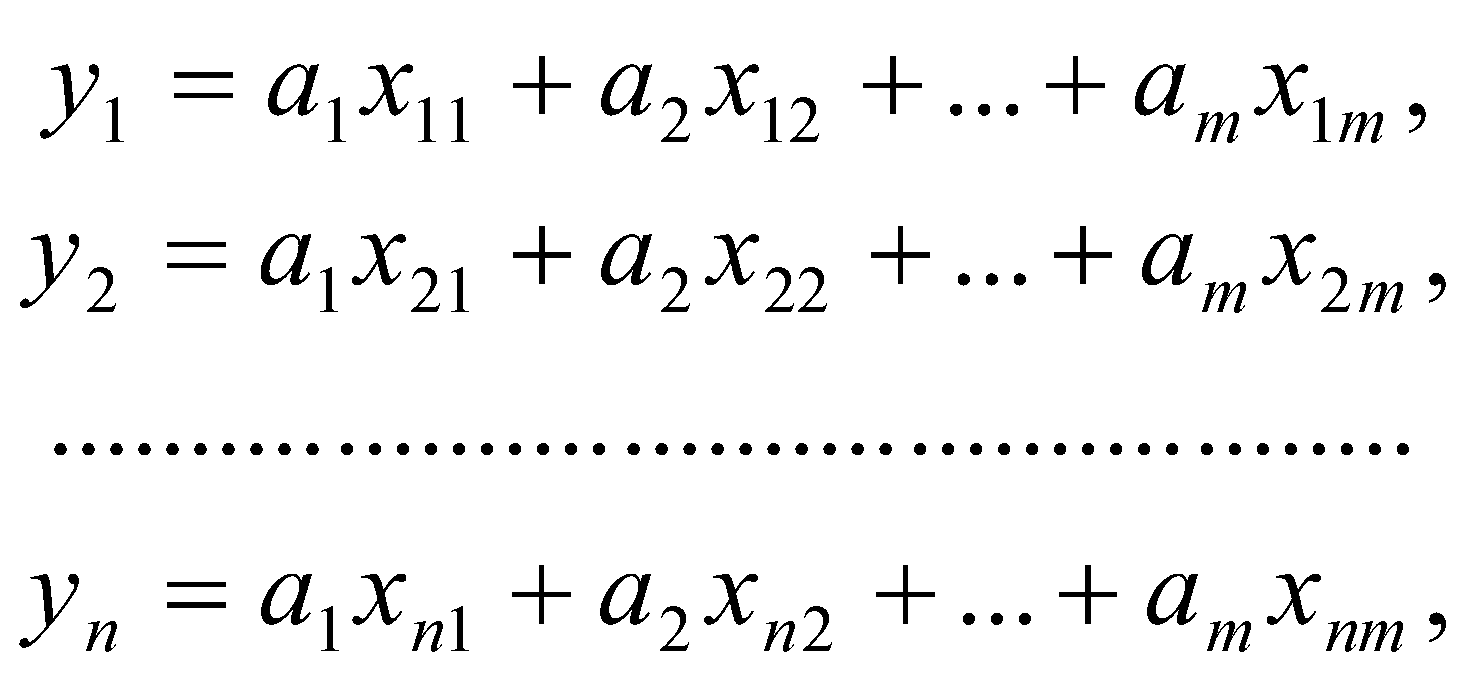(35)

здесь –измеряемые значения величины , –известные значения аргумента.

Систему уравнений (35) перепишем в виде

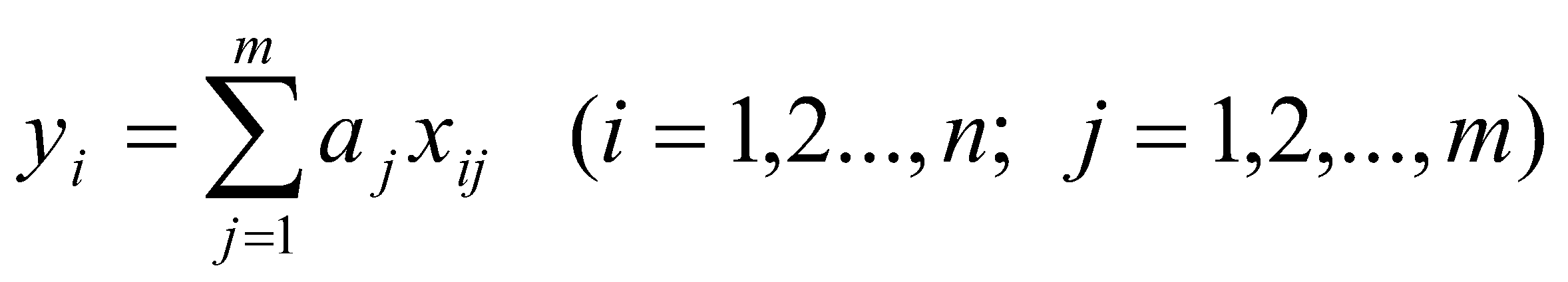(36)

Так как измерены с некоторой погрешностью

---

то действительный результат измерения будет иметь вид

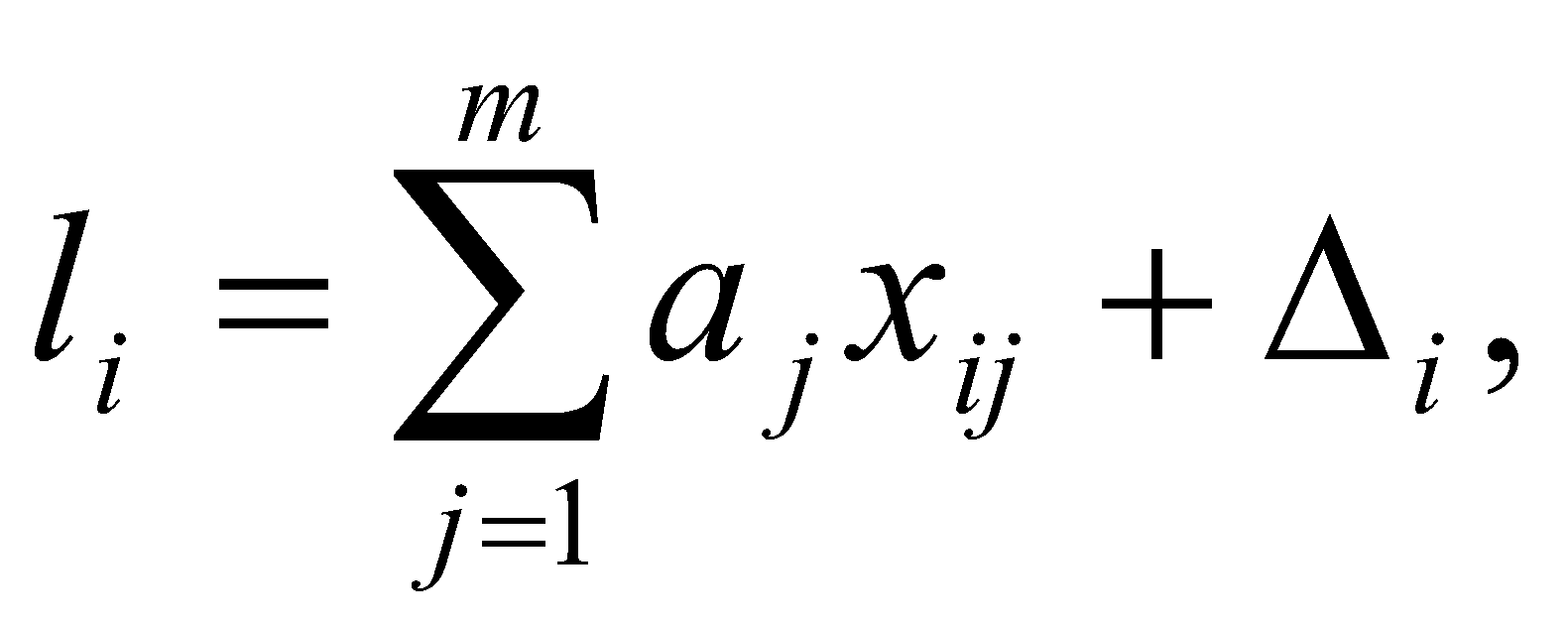(37)

или



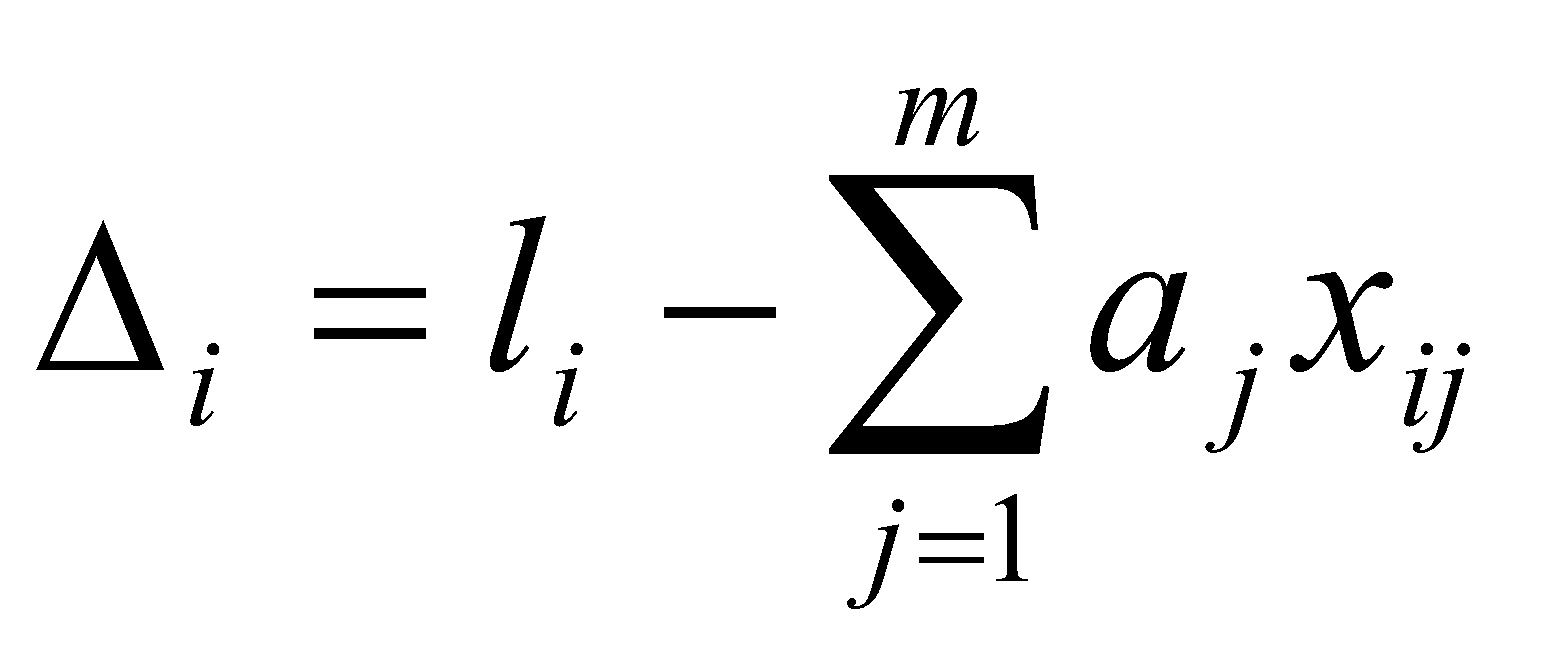
В соответствии с МНК наилучшие оценки для должны соответствовать условию



или

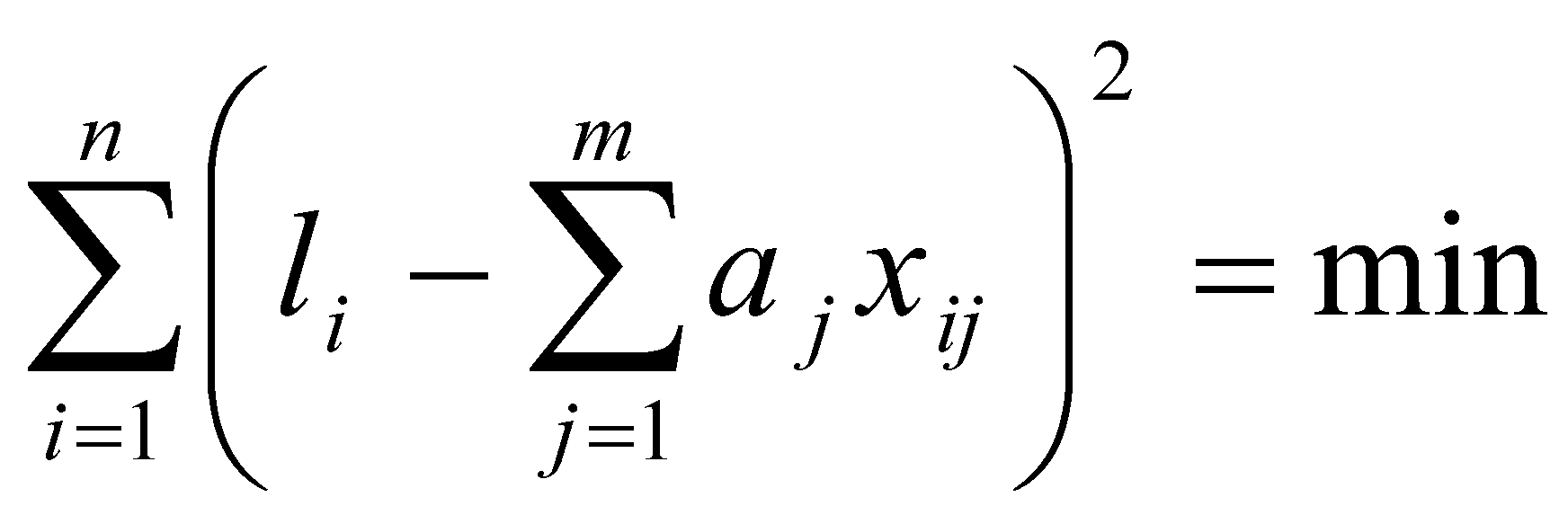. (38)

Это условие выполняется, если все частные производные от (2.38) по искомым параметрам будут равны нулю, т. е.

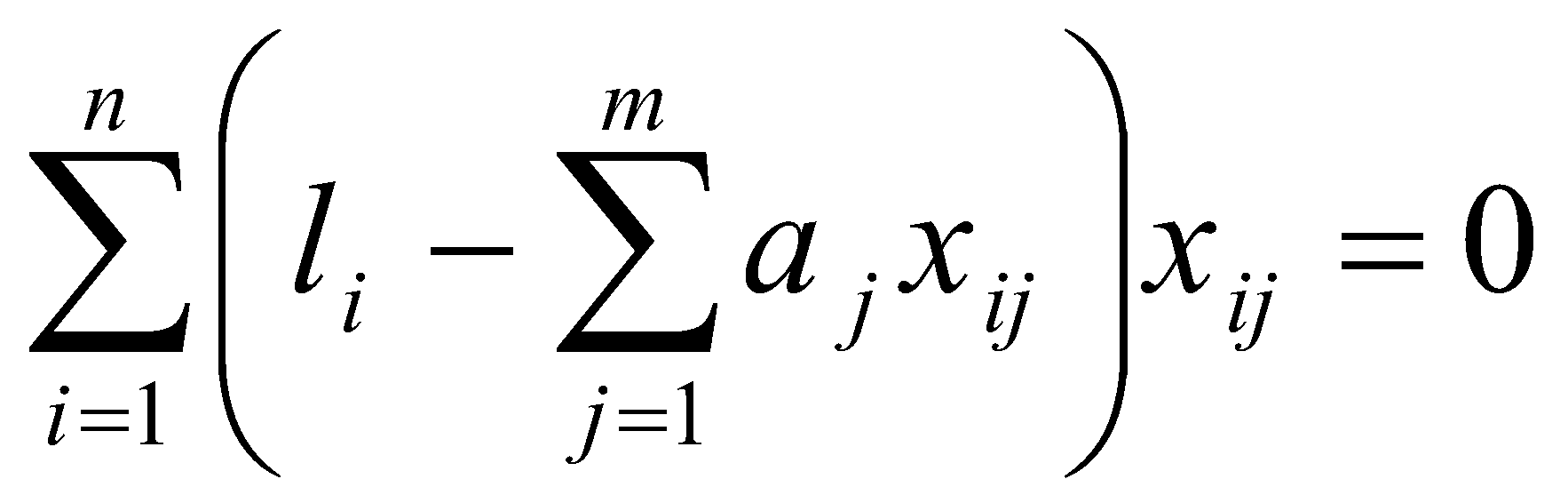. (39)

Система уравнений (39) линейна относительно , решая ее известными методами определяем искомые параметры постулируемой модели (35). Оценки параметров является состоятельными, несмещенными и эффективными.

Оценка дисперсии случайной погрешности согласно [2.8] будет равна

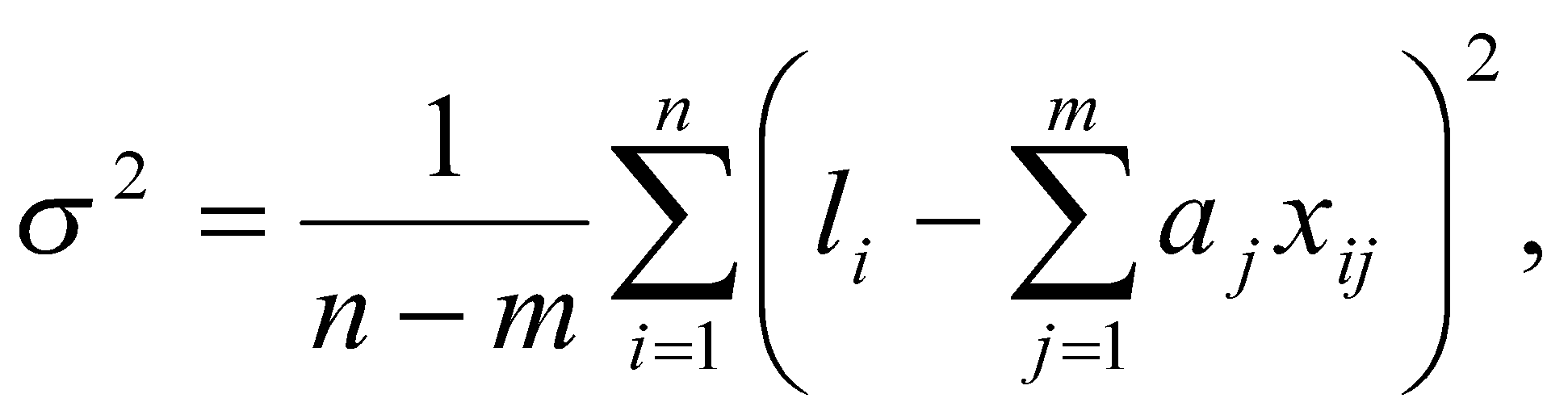(40)

здесь – измеренные величины, соответствующие ; –коэффициенты, найденные по (39).

При обработке экспериментального материала с целью определения функции преобразования в качестве математической модели часто выбирают полином вида:



а задачей самого измерения является определение коэффициентов

---

Смотрите также файлы

• Секстуризм где клубничка вкуснее.pptx

• Отчет по научноисследовательской работе магистранта специальности 6М072400 технологические машины и оборудование.docx

• Хищники.pptx

• Законы экологии. Факторы, влияющие на состояние здоровья человека. Экосистемы, их структура и организация. Биосфера, ноосфера.docx

• Госпожа Пенициллин Презентацию подготовила студентка 1 курса.pptx