Файл: Анализ методов кодирования данных Автор Анна Евкова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 91
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Глава 2.Кодирование информации в системе обработки информации
2.1. Кодирование текстовой информации
В процессе обработки информации, т.е. преобразования информации из одной формы представления (знаковой системы) в другую осуществляется кодирование. Средством кодирования служит таблица соответствия, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем. При вводе знака алфавита в компьютер путем нажатия соответствующей клавиши на клавиатуре выполняется его кодирование, т. е. преобразование в компьютерный код. При выводе знака на экран монитора или принтер происходит обратный процесс — декодирование, когда из компьютерного кода знак преобразуется в графическое изображение.
Текст состоит из символов, поэтому символ можно считать минимальным элементом текста. Если собрать все возможные символы, которые могут встретиться в тексте: латинские буквы, буквы кириллицы, знаки препинания и т. д., и каждому из этих символов присвоить свой уникальный номер (код символа), то текст можно записать в виде набора чисел.
Для хранения кода одного символа может быть выделен один байт. С помощью одного байта можно закодировать 256 различных символов, учитывая, что каждый бит принимает значение 0 или 1, и количество их возможных сочетаний в байте равно 28=256. Этого вполне достаточно для представления текстовой информации, включая прописные и строчные буквы русского и латинского алфавитов, цифры, знаки, псевдографические символы и т. д [19, с.24].
Кодирование заключается в том, что каждому символу ставится в соответствие уникальный десятичный код от 0 до 255 или соответствующий ему двоичный код от 00000000 до 11111111. Таким образом, человек различает символы по их начертанию, а компьютер — по их коду. Важно, что присвоение символу конкретного кода — это вопрос соглашения, которое фиксируется в кодовой таблице.
Технически это выглядит очень просто, однако всегда существовали достаточно веские организационные сложности. В первые годы развития вычислительной техники они были связаны с отсутствием необходимых стандартов, а в настоящее время вызваны, наоборот, изобилием одновременно действующих и противоречивых стандартов. Для того чтобы весь мир одинаково кодировал текстовые данные, нужны единые таблицы кодирования, а это пока невозможно из-за противоречий между символами национальных алфавитов, а также противоречий корпоративного характера.
Существует несколько различных стандартов кодирования символов, но первоосновой для всех стал стандарт ASCII (American Standard Code for Information Interchange — американский стандартный код для информационного обмена).
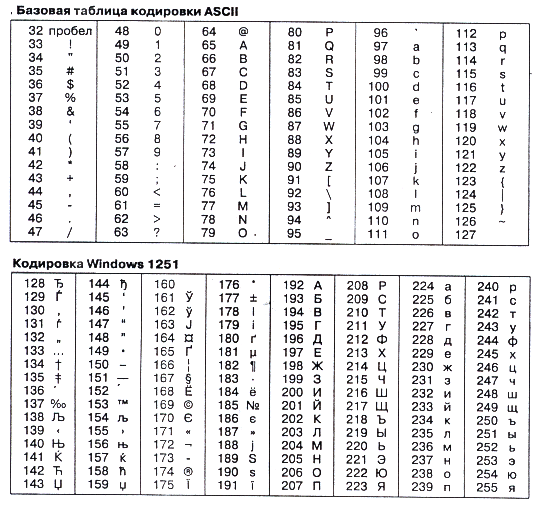
В ASCII закреплены две таблицы кодирования: базовая и расширенная. В базовой таблице определены значения кодов с 0 по 127, а в расширенной — с 128 по 255. В базовой таблице находятся символы латинского алфавита, цифры, знаки арифметических операций и знаки препинания (табл. 1.1). Кроме того, за кодами с 0 по 32 закреплены специальные функции: перевод строки, ввод пробела и т. д. Расширенная таблица содержит символы национальных алфавитов различных стран мира и так называемые символы псевдографики, с помощью которых можно, например, рисовать таблицы [19, с.25].

Рис.2.1 Таблица кодов ASCII (расширенная)
Для языков, использующих кириллицу, в том числе и для русского, пришлось полностью менять вторую половину таблицы ASCII, приспосабливая её под кириллический алфавит. В частности, для представления символов кириллицы используется так называемая «альтернативная кодировка».
Альтернативная кодировка не подошла для ОС Windows. Пришлось передвинуть русские буквы в таблице на место псевдографики, и получили кодировку Windows 1251 (Win-1251). Кодировка символов русского языка, известная как кодировка Windows-1251, была введена «извне» - компанией Microsoft, но, учитывая широкое распространение операционных систем и других продуктов этой компании в России, она глубоко закрепилась и нашла широкое распространение.
Сейчас существует несколько различных кодовых таблиц для русских букв (КОИ-8, СР-1251, СР-866, Мае, ISO), причём тексты, созданные в одной кодировке, могут совершенно неправильно отображаться в другой. Решается такая проблема с помощью специальных программ перевода текста из одной кодировки в другую [4. c.67].
Другая распространённая кодировка носит название КОИ-8 (код обмена информацией, восьмизначный) – её происхождение относится к временам действия Совета Экономической Взаимопомощи государств Восточной Европы. Сегодня кодировка КОИ – 8 имеет широкое распространение в компьютерных сетях на территории России и в российском секторе Интернета.
Международный стандарт, в котором предусмотрена кодировка символов русского языка, носит названия ISO (International Standard Organization – Международный институт стандартизации). На практике данная кодировка используется редко.
Если проанализировать организационные трудности, связанные с созданием единой системы кодирования текстовых данных, то можно прийти к выводу, что они вызваны ограниченным набором кодов (256). Математикам требуется использовать в формулах специальные математические знаки, переводчикам необходимо создавать тексты, где могут встретиться символы из различных алфавитов, экономистам необходимы символы валют ($, F, А). Для решения этой проблемы была разработана универсальная система кодирования текстовой информации — UNICODE. В этой кодировке для каждого символа отводится не один, а два байта, то есть шестнадцать битов. Очевидно, что если, кодировать символы не восьмиразрядными двоичными числами, а числами с большим разрядом то и диапазон возможных значений кодов станет на много больше. Шестнадцать разрядов позволяют обеспечить уникальные коды для 65536 различных символов – этого поля вполне достаточно для размещения в одной таблице символов большинства языков планеты. Этого хватает на латинский алфавит, кириллицу, иврит, африканские и азиатские языки, различные специализированные символы: математические, экономические, технические и многое другое.
Несмотря на тривиальную очевидность такого подхода, простой механический переход на данную систему долгое время сдерживался из-за недостатков ресурсов средств вычислительной техники (в системе кодирования UNICODE все текстовые документы становятся автоматически вдвое длиннее). Но во второй половине 90-х годов технические средства достигли необходимого уровня обеспечения ресурсами, и сегодня мы наблюдаем постепенный перевод документов и программных средств на универсальную систему кодирования UNICODE.
2.2. Кодирование целых и действительных чисел
Естественным представлением целого неотрицательного числа является двоичная система счисления. Кодирование отрицательных чисел производится тремя наиболее употребительными способами, в каждом из которых крайний левый бит - знаковый. Отрицательному числу соответствует единичный бит, а положительному - нулевой.
1. Прямой код. Изменение знака производится просто, путем инверсии бита знака. Пусть 00001001 = 9, тогда 10001001 = -9. Если при сложении двух чисел в этом коде знаки совпадают, то трудностей нет. Если знаки различаются необходимо найти наибольшее число, вычесть из него меньшее, а результату присвоить знак наибольшего слагаемого.
2. Обратный код, инверсный или дополнительный "до 1". Изменение знака производится просто - инверсией всех бит: 00001001 = 9, а 11110110 = - 9. Сложение также выполняется просто, т.к. знаковые биты можно складывать. При переносе единицы из левого (старшего) бита, она должна складываться с правым (младшим). Например: 7 + (-5) = 2.
00000111 = 7
11111010 =-5 (инверсия 00000101 = 5)
1 00000001
1
00000010 = 2
Сложение в обратном коде происходит быстрее, т.к. не требуется принятие решения, как в предыдущем случае. Однако суммирование бита переноса требует дополнительных действий. Другим недостатком этого кода является представление нуля двумя способами, т.к. инверсия 0...00 равна 1...11 и сумма двух разных по знаку, но равных по значению чисел дает 1...11. Например: (00001001 = 9) + (11110110 = -9) = 11111111. Кстати, из этого примера понятно, почему код называется дополнительным "до 1". Этих недостатков лишен код, дополнительный до 2.
3. Дополнительный или дополнительный "до 2" код. Число с противоположным знаком находится инверсией исходного и добавлением к результату единицы. Например, найти код числа -9.
00001001 = 9 11110111 =-9
11110110 - инверсия 00001000 - инверсия
1 1
11110111 =-9 00001001 = 9
Проблемы двух нулей нет. +0 = 00000000, -0 = 11111111 + 1 = 00000000 (перенос из старшего бита не учитывается).Сложение производится по обычным для неотрицательных чисел правилам.
00001001 = 9
11110111 =-9
1 00000000
Из этого примера видно, что в каждом разряде двух равных по модулю чисел складываются две единицы, что и определило название способа. Этот метод применяется наиболее часто, и когда говорят о дополнительном коде, то имеется в виду дополнительный "до 2-х" код.
Примеры однобайтных целых чисел:
Числа с плавающей точкой. Вещественные числа хранятся в показательной форме, т.е. в виде двух составляющих: мантиссы и порядка. Различия в способах такого представления чисел заключаются в количестве байтов, отводимых под порядок и мантиссу и небольших отличиях в форме их хранения. Например в четырехбайтовом формате под мантиссу отводится 3 байта и один байт для хранения порядка (КВ - короткий вещественный формат):
Пример одного из вариантов формата:
Старший разряд старшего байта хранит знак мантиссы, следующий за ним - знак порядка.
В другом варианте знак мантиссы может храниться в старшем разряде байта 2, а сам порядок храниться в "смещенной" форме, в виде числа Е‑127.
Тогда представление числа D: D = ±M * 2^(E-127), где мантисса, Е – смещенный порядок, хранящийся в старшем байте. При этом может быть принято соглашение о неявном присутствии единицы слева от десятичной точки, так что мантисса будет принимать значения от 1 до 2. Соответственно в зависимости от вариаций формата будут слегка отличаться и диапазоны представления чисел. Так, в последнем варианте, где у нормализованной мантиссы первая значащая цифра (единица) мысленно находится слева от запятой, а справа располагаются 23 разряда - 1,xx..xx, Mmax = 1,111..11 = 1 +1/2 +1/4+ 1/8 +...= 2, а Mmin= 1,000..00 = 1 для положительных чисел (SM=0) и -1 и -2 для отрицательных, (SM=1). Порядок числа Emax = 11111110 = 254, а Emin = 00000001 = 1. Теперь можно определить диапазон представления положительных чисел от +Dmax = Mmax * 2(254-127) = 3,4 * 1038 до +Dmin = Mmin * 2(1-127) = 1,17 * 10-38. Точность определяется числом достоверных десятичных цифр. При 23 двоичных разрядах мантиссы 223 примерно равно 107, т.е. достоверными являются только 6-7 значащих десятичных знаков, а не 38. Необходимо отметить, что значения порядка 11111111 и 00000000 по международным стандартам IEEE 754 и IEEE 854 предназначены для кодирования денормализованных чисел, отрицательной и положительной бесконечностей, неопределенности и так называемых "Не-чисел" [7, c.89].
2.1. Кодирование текстовой информации
В процессе обработки информации, т.е. преобразования информации из одной формы представления (знаковой системы) в другую осуществляется кодирование. Средством кодирования служит таблица соответствия, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем. При вводе знака алфавита в компьютер путем нажатия соответствующей клавиши на клавиатуре выполняется его кодирование, т. е. преобразование в компьютерный код. При выводе знака на экран монитора или принтер происходит обратный процесс — декодирование, когда из компьютерного кода знак преобразуется в графическое изображение.
Текст состоит из символов, поэтому символ можно считать минимальным элементом текста. Если собрать все возможные символы, которые могут встретиться в тексте: латинские буквы, буквы кириллицы, знаки препинания и т. д., и каждому из этих символов присвоить свой уникальный номер (код символа), то текст можно записать в виде набора чисел.
Для хранения кода одного символа может быть выделен один байт. С помощью одного байта можно закодировать 256 различных символов, учитывая, что каждый бит принимает значение 0 или 1, и количество их возможных сочетаний в байте равно 28=256. Этого вполне достаточно для представления текстовой информации, включая прописные и строчные буквы русского и латинского алфавитов, цифры, знаки, псевдографические символы и т. д [19, с.24].
Кодирование заключается в том, что каждому символу ставится в соответствие уникальный десятичный код от 0 до 255 или соответствующий ему двоичный код от 00000000 до 11111111. Таким образом, человек различает символы по их начертанию, а компьютер — по их коду. Важно, что присвоение символу конкретного кода — это вопрос соглашения, которое фиксируется в кодовой таблице.
Технически это выглядит очень просто, однако всегда существовали достаточно веские организационные сложности. В первые годы развития вычислительной техники они были связаны с отсутствием необходимых стандартов, а в настоящее время вызваны, наоборот, изобилием одновременно действующих и противоречивых стандартов. Для того чтобы весь мир одинаково кодировал текстовые данные, нужны единые таблицы кодирования, а это пока невозможно из-за противоречий между символами национальных алфавитов, а также противоречий корпоративного характера.
Существует несколько различных стандартов кодирования символов, но первоосновой для всех стал стандарт ASCII (American Standard Code for Information Interchange — американский стандартный код для информационного обмена).
В ASCII закреплены две таблицы кодирования: базовая и расширенная. В базовой таблице определены значения кодов с 0 по 127, а в расширенной — с 128 по 255. В базовой таблице находятся символы латинского алфавита, цифры, знаки арифметических операций и знаки препинания (табл. 1.1). Кроме того, за кодами с 0 по 32 закреплены специальные функции: перевод строки, ввод пробела и т. д. Расширенная таблица содержит символы национальных алфавитов различных стран мира и так называемые символы псевдографики, с помощью которых можно, например, рисовать таблицы [19, с.25].

Рис.2.1 Таблица кодов ASCII (расширенная)
Для языков, использующих кириллицу, в том числе и для русского, пришлось полностью менять вторую половину таблицы ASCII, приспосабливая её под кириллический алфавит. В частности, для представления символов кириллицы используется так называемая «альтернативная кодировка».
Альтернативная кодировка не подошла для ОС Windows. Пришлось передвинуть русские буквы в таблице на место псевдографики, и получили кодировку Windows 1251 (Win-1251). Кодировка символов русского языка, известная как кодировка Windows-1251, была введена «извне» - компанией Microsoft, но, учитывая широкое распространение операционных систем и других продуктов этой компании в России, она глубоко закрепилась и нашла широкое распространение.

Сейчас существует несколько различных кодовых таблиц для русских букв (КОИ-8, СР-1251, СР-866, Мае, ISO), причём тексты, созданные в одной кодировке, могут совершенно неправильно отображаться в другой. Решается такая проблема с помощью специальных программ перевода текста из одной кодировки в другую [4. c.67].
Другая распространённая кодировка носит название КОИ-8 (код обмена информацией, восьмизначный) – её происхождение относится к временам действия Совета Экономической Взаимопомощи государств Восточной Европы. Сегодня кодировка КОИ – 8 имеет широкое распространение в компьютерных сетях на территории России и в российском секторе Интернета.
Международный стандарт, в котором предусмотрена кодировка символов русского языка, носит названия ISO (International Standard Organization – Международный институт стандартизации). На практике данная кодировка используется редко.
Если проанализировать организационные трудности, связанные с созданием единой системы кодирования текстовых данных, то можно прийти к выводу, что они вызваны ограниченным набором кодов (256). Математикам требуется использовать в формулах специальные математические знаки, переводчикам необходимо создавать тексты, где могут встретиться символы из различных алфавитов, экономистам необходимы символы валют ($, F, А). Для решения этой проблемы была разработана универсальная система кодирования текстовой информации — UNICODE. В этой кодировке для каждого символа отводится не один, а два байта, то есть шестнадцать битов. Очевидно, что если, кодировать символы не восьмиразрядными двоичными числами, а числами с большим разрядом то и диапазон возможных значений кодов станет на много больше. Шестнадцать разрядов позволяют обеспечить уникальные коды для 65536 различных символов – этого поля вполне достаточно для размещения в одной таблице символов большинства языков планеты. Этого хватает на латинский алфавит, кириллицу, иврит, африканские и азиатские языки, различные специализированные символы: математические, экономические, технические и многое другое.
Несмотря на тривиальную очевидность такого подхода, простой механический переход на данную систему долгое время сдерживался из-за недостатков ресурсов средств вычислительной техники (в системе кодирования UNICODE все текстовые документы становятся автоматически вдвое длиннее). Но во второй половине 90-х годов технические средства достигли необходимого уровня обеспечения ресурсами, и сегодня мы наблюдаем постепенный перевод документов и программных средств на универсальную систему кодирования UNICODE.
2.2. Кодирование целых и действительных чисел
Естественным представлением целого неотрицательного числа является двоичная система счисления. Кодирование отрицательных чисел производится тремя наиболее употребительными способами, в каждом из которых крайний левый бит - знаковый. Отрицательному числу соответствует единичный бит, а положительному - нулевой.
1. Прямой код. Изменение знака производится просто, путем инверсии бита знака. Пусть 00001001 = 9, тогда 10001001 = -9. Если при сложении двух чисел в этом коде знаки совпадают, то трудностей нет. Если знаки различаются необходимо найти наибольшее число, вычесть из него меньшее, а результату присвоить знак наибольшего слагаемого.
2. Обратный код, инверсный или дополнительный "до 1". Изменение знака производится просто - инверсией всех бит: 00001001 = 9, а 11110110 = - 9. Сложение также выполняется просто, т.к. знаковые биты можно складывать. При переносе единицы из левого (старшего) бита, она должна складываться с правым (младшим). Например: 7 + (-5) = 2.
00000111 = 7
11111010 =-5 (инверсия 00000101 = 5)
1 00000001
1
00000010 = 2
Сложение в обратном коде происходит быстрее, т.к. не требуется принятие решения, как в предыдущем случае. Однако суммирование бита переноса требует дополнительных действий. Другим недостатком этого кода является представление нуля двумя способами, т.к. инверсия 0...00 равна 1...11 и сумма двух разных по знаку, но равных по значению чисел дает 1...11. Например: (00001001 = 9) + (11110110 = -9) = 11111111. Кстати, из этого примера понятно, почему код называется дополнительным "до 1". Этих недостатков лишен код, дополнительный до 2.
3. Дополнительный или дополнительный "до 2" код. Число с противоположным знаком находится инверсией исходного и добавлением к результату единицы. Например, найти код числа -9.
00001001 = 9 11110111 =-9
11110110 - инверсия 00001000 - инверсия
1 1
11110111 =-9 00001001 = 9
Проблемы двух нулей нет. +0 = 00000000, -0 = 11111111 + 1 = 00000000 (перенос из старшего бита не учитывается).Сложение производится по обычным для неотрицательных чисел правилам.
00001001 = 9
11110111 =-9
1 00000000
Из этого примера видно, что в каждом разряде двух равных по модулю чисел складываются две единицы, что и определило название способа. Этот метод применяется наиболее часто, и когда говорят о дополнительном коде, то имеется в виду дополнительный "до 2-х" код.
Примеры однобайтных целых чисел:
| D7 | D6 | D5 | D4 | D3 | D2 | D1 | D0 | Целое двоичное без знака (256 чисел) | |
| | | | | | | | | | |
| S | D6 | D5 | D4 | D3 | D2 | D1 | D0 | Целое двоичное co знаком (от ‑27 до | |
| | | | | | | | | +(27‑1) | |
| D3 | D2 | D1 | D0 | D3 | D2 | D1 | D0 | Десятичное двоично-кодированное | |
| старшая цифра | младшая цифра | (упакованный формат) | |||||||
Числа с плавающей точкой. Вещественные числа хранятся в показательной форме, т.е. в виде двух составляющих: мантиссы и порядка. Различия в способах такого представления чисел заключаются в количестве байтов, отводимых под порядок и мантиссу и небольших отличиях в форме их хранения. Например в четырехбайтовом формате под мантиссу отводится 3 байта и один байт для хранения порядка (КВ - короткий вещественный формат):
Пример одного из вариантов формата:
| байт 3 | байт 2 | байт 1 | байт 0 | ||||||||||||||||||||||||||||||
| s | s | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |||
| | | порядок | мантисса (от 2-1 до 1) | ||||||||||||||||||||||||||||||
Старший разряд старшего байта хранит знак мантиссы, следующий за ним - знак порядка.
В другом варианте знак мантиссы может храниться в старшем разряде байта 2, а сам порядок храниться в "смещенной" форме, в виде числа Е‑127.
Тогда представление числа D: D = ±M * 2^(E-127), где мантисса, Е – смещенный порядок, хранящийся в старшем байте. При этом может быть принято соглашение о неявном присутствии единицы слева от десятичной точки, так что мантисса будет принимать значения от 1 до 2. Соответственно в зависимости от вариаций формата будут слегка отличаться и диапазоны представления чисел. Так, в последнем варианте, где у нормализованной мантиссы первая значащая цифра (единица) мысленно находится слева от запятой, а справа располагаются 23 разряда - 1,xx..xx, Mmax = 1,111..11 = 1 +1/2 +1/4+ 1/8 +...= 2, а Mmin= 1,000..00 = 1 для положительных чисел (SM=0) и -1 и -2 для отрицательных, (SM=1). Порядок числа Emax = 11111110 = 254, а Emin = 00000001 = 1. Теперь можно определить диапазон представления положительных чисел от +Dmax = Mmax * 2(254-127) = 3,4 * 1038 до +Dmin = Mmin * 2(1-127) = 1,17 * 10-38. Точность определяется числом достоверных десятичных цифр. При 23 двоичных разрядах мантиссы 223 примерно равно 107, т.е. достоверными являются только 6-7 значащих десятичных знаков, а не 38. Необходимо отметить, что значения порядка 11111111 и 00000000 по международным стандартам IEEE 754 и IEEE 854 предназначены для кодирования денормализованных чисел, отрицательной и положительной бесконечностей, неопределенности и так называемых "Не-чисел" [7, c.89].