Федеральное государственное образовательное бюджетноеучреждение высшего образования«Финансовый университет при Правительстве Российской Федерации»(Финансовый университет)Краснодарский филиал ФинуниверситетаКафедра «Математика и информатика»КОНТРОЛЬНАЯ РАБОТАпо дисциплине «Финансовая математика»Вариант 4Номер зачетной книжки 100.13/200254Выполнил студент учебной группыКРНД20-ЭК-УА-иуп-зВоробьева Владислава ВладиславовнаКраснодар 2023Выбор варианта – по последней цифре номера зачетной книжкиТема 1. Простые проценты1.4. Банк выдал кредит 15 января в размере 200,0 тыс. руб. Срок возврата кредита – 20 марта; процентная ставка – 12,0% годовых; год невисокосный. Определить сумму долга, подлежащую возврату. Рассчитать ее тремя методами.Решение:Определим точное число дней ссуды:с 15 января по 31 января – 22 дня,в феврале – 28 дней,в марте с 1 марта по 20 марта -20 дней,Итого: 70 днейВычитаем 1 день, так как день выдачи и день погашения принимается за один.Следовательно, t = 69 дней.

1. 
   по точным процентам с точным числом дней ссуды:
   

S=200(1+ 69/365*0,12)=200*1,02268493=204,54 тыс. руб

2. 
   по обыкновенным процентам с точным числом дней ссуды:
   

S=200(1+69/360*0,12)=200*1,023=204,6 тыс. руб

3. 
   по обыкновенным процентам с приближенным числом дней ссуды:
   

S=200(1+70/365*0,12)=200*1,0230137=204,60274 тыс. руб Приведенные решения свидетельствуют о том, что для кредиторов наиболее предпочтительным является третий вариант начисления процентов.Между величинами процентного дохода, рассчитанными с использованием различной временной базы (I360 и I365) при равном числе дней ссуды (t) существуют следующие соотношения:360/365=1,01388 365/360=0,9863Тема 2. Сложные проценты2.4. Клиент внес в банк 30 тыс. руб. под 12 % годовых. Через 2 года и 270 дней он изъял вклад. Определить полученную им сумму при использовании банком сложных процентов и смешанного метода, при временной базе

---

.
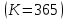
* Клиент внес в банк 2,5 тыс. руб. под 9,5% годовых, через
2 года и 270 дней он изъял вклад. Определить полученную им
сумму при использовании банком:
а) сложных процентов;
б) смешанного метода.

Определим наращенную сумму по формуле:

Sn = P * (1 + rc)a * (1 + b * rc) ,где:

Sn – наращенная сумма, тыс. руб.;

P – первоначальная сумма, тыс. руб.;

a – целое число периодов, лет;

b – дробная часть периода, дни;

rc – процентная ставка, %

а) S = 2г270дн= 30 *(1 + 0,12) ^2 +(270/365)= 40,9704576 тыс. руб.;
б) S = 2г270дн=30* (1,12) ^2 * (1 + 270/365*0,12) =(30*1,2544)*(1,08876) = 40,97 тыс. руб.
Ответ. При использовании банком сложных процентов и смешанного метода начисления процентов через 2 года и 270 дней клиент получит 40,97 тыс руб.
Тема 3. Эквивалентность ставок.

Изменение условий коммерческих сделок
3.4. Ссуда выдана на 2 года под 12,0 % годовых (процент простые). Определить эквивалентную ей ставку сложных процентов

Эквивалентность простой ставки процентов и учетной ставки определяется равенством:

1+i*n = (1 - n*d) -1, откуда

i=d/(1-n*d)

d=i/(1+i*n).

Эквивалентность простой и сложной ставки процентов рассчитывается из равенства:

1+ic=(1+iп/m)m*n, откуда

ic=(1+ iп/m) m*n -1

Решение:

iс =((1 + 0,12/2)^2)-1 = (1,06^2) -1= 1,1236-1= 0,1236 или 12.36%
Ответ: 0,1236 или 12.36%

Тема 4. Погашение среднесрочных и долгосрочных кредитов
4.4. Кредит размером 8,0 млн. руб. выдан на 5 лет под 15 % годовых с начислением процентов в конце каждого расчетного периода (года). Выплаты основного долга должны возрастать ежегодно 0,2 млн. руб.

Составить план погашения кредита.

год	Остаток долга на начало года	Сумма погашения основного долга	Сумма выплат процентов	Сумма срочных уплат
1	8
2
3
4
5	0

---

Q=0,2 Одним из вариантов погашения кредитной задолженности может быть такой, при котором погашение основного долга должно произ­водиться платежами, каждый из которых больше или меньше преды­дущего в q раз. Таким образом, эти платежи будут являться членами возрастающей или убывающей геометрической прогрессии. Члены этой прогрессии будут иметь вид: 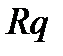 ,  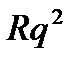,  , …. Основной долг – сумма этих членов, т.е.  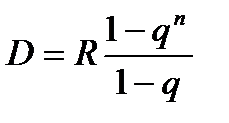, откуда  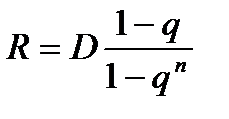 (первый платеж по основному долгу).Составьте план погашения кредита, выданного в размере 185 000 тыс. руб. на 6 месяцев под 19% годовых. Погашение кредита осуществляется равными ежемесячными платежами. 

Решение:

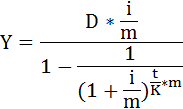
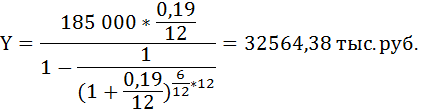
Рассчитать ежемесячный платёж можно по формуле:гдеY – сумма ежемесячного платежа,D – сумма кредита (основной долг),i – процентная ставка, в коэффициентах (0,19 = 19% / 100%),m – число начислений процентов в течение года,t – срок погашения в месяцах.Сумма ежемесячного платежа по кредиту составит:Эта сумма включает процентный платёж, который в первый месяц рассчитывается на всю величину долга:185 000 × 0,19 / 12 = 2929,17 тыс. руб.и месячную сумму основного долга:32564,38 – 2929,17 = 29635,21 тыс. руб.На эту сумму уменьшится основная сумма долга. Теперь основная сумма долга составит:185 000 – 29635,21 = 155364,8 тыс. руб.Во второй месяц ежемесячный платёж остался прежним – 32564,38 тыс. руб., а вот процентный платёж снизится, так как будет рассчитан от величины оставшейся основной суммы долга:

---

155364,8 × 0,19 / 12 = 2459,94 тыс. руб.Соответственно на долю месячной суммы основного долга приходится32564,38 – 2459,94 = 30104,44 и т.д.За полгода будет выплачено32 564,38 × 6 = 195 386,3 тыс. руб.Составим план погашения кредита:

№ п/п	Сумма ежемесячного платежа, тыс. руб.	Месячная выплата основного долга, тыс. руб.	Процентные платежи, тыс. руб.	Непогашенная сумма основного долга, тыс. руб.
0	-	-	-	185 000,00
1	32 564,38	29 635, 21	2 929,17	155 364,79
2	32 564,38	30 104,44	2 459,94	125 260,35
3	32 564,38	30 581,09	1 983,29	94 679,26
4	32 564,38	31 065,29	1 499,09	63 613,97
5	32 564,38	31 557,16	1 007,22	32 056,81
6	32 564,38	32 056,81	507,57	0,00
Итого по кредиту	195 386,27	185 000,00	10 386,27	-

Пример оформления1.2.Владелец векселя номинальной стоимостью 220 тыс. руб. и сроком обращения один год предъявил его банку-эмитенту для учета за 90 дней до даты погашения. Банк учел его по ставке 12,0%. Определить дисконтированную величину, т.е. сумму, полученную владельцем векселя 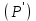и величину дисконта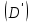

---

Решение:1) Сумма, полученная владельцем векселя, составит: 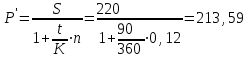тыс. руб.2) Величина дисконта составит 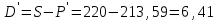тыс. руб.Используя приведенные ранее формулы, рассчитаем величину эффективной годовой процентной ставки, отражающей реальный доход, т.е. ставки, по которой были фактически начислены проценты на первоначальную сумму.Если 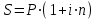,то 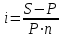или 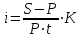где 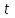– срок ссуды в днях; 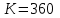ил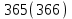и дней.Для нашего случая 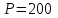тыс. руб. – сумма, заплаченная за вексель в момент его приобретения. Дисконтированная величина 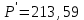тыс. руб. для владельца векселя является наращенной за 270 дней суммой. Тогда эффективная ставка равна: 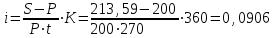или 9,06 %

---

Смотрите также файлы

• Решение Эффективность способность приносить эффект результативность процесса отношение результата к затратам.docx

• Республики казахстан ао академия гражданской авиации.docx

• Стратегия управления кадровым потенциалом Школы Минпросвещения России.docx

• "Понятие экоинноваций".pdf

• Административная и уголовная ответственность в области трудового законодательства.docx