Файл: Петухов Михаил Николаевич гр. Дмп 102уцп Проверил Гумеров Э. А. Москва 2022 Задание Тема Алгоритмы гладкой однокритериальной оптимизации. Лабораторный практикум.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 61
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ ЧАСТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ФИНАНСОВО-ПРОМЫШЛЕННЫЙ УНИВЕРСИТЕТ «СИНЕРГИЯ»
Институт Информационных технологий
Отчёт по лабораторной работе №1
По дисциплине:
«Системы поддержи принятия решений»
Обучающийся
Петухов Михаил Николаевич
гр. ДМП 102-уцп
Проверил
Гумеров Э.А.
Москва
2022
Задание:
Тема 2. Алгоритмы «гладкой» однокритериальной оптимизации.
Лабораторный практикум №1.
ЛПР выбирает адвоката для представления его интересов в суде. В качестве альтернатив у него имеются адвокаты А1, А2, А3 и А4. В качестве критериев выступают: Стоимость (К1), Авторитет (К2), Репутация (К3), Специализация (К4). Оценки показателей привлекательностей каждого адвоката (альтернативы) по каждому критерию, а также веса критериев по десятибалльной системе представлены матрицей 1 в прилагемом файле.
Решение:
| | K1 | K2 | K3 | K4 | ∑ | |
| A1 | 3 | 7 | 2 | 9 | 162 | |
| A2 | 8 | 3 | 6 | 7 | 176 | |
| A3 | 4 | 8 | 3 | 5 | 157 | |
| A4 | 9 | 6 | 5 | 4 | 184 | |
| Вес | 8 | 9 | 6 | 7 | | |
Для выбора наиболее эффективного адвоката (А), нам необходимо по каждому произвести расчет по следующей формуле: произведение критерия конкретного адвоката на вес данного критерия.
F1=3*8+7*9+2*6+9*7=162
F2=8*8+3*9+6*6+7*7=176
F3=4*8+8*9+3*6+5*7=157
F4=9*8+6*9+5*6+4*7=184
По критерию Лапласа лучшим адвокатом является тот, у которого- максимальная оценка.
В нашем случае это-адвокат №4 (184).
По критерию Вальда с максимальной оценкой также лидирует адвокат №4.
По критерию Сэвиджа лучшим является решение с максимальной оценкой, также №4.
Критерий Лапласа, Вальда, Сэвиджа, Гурвица
Существует несколько критериев для выбора оптимальной стратегии при принятии решения в условиях риска и неопределенности.
Критерий Лапласа:применяется, если можно предполагать, что все варианты внешних условий одинаково вероятны. Для каждого решения находится средняя оценка по всем вариантам внешних условий (средний выигрыш):
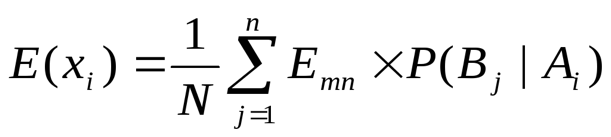
где N– количество состояний внешней среды.
Лучшим является решение с максимальной оценкой.
где Z – оптимальная стратегия.
Критерий Вальда: (критерий крайнего пессимизма, максиминный критерий): решение выбирается в расчете на наихудшие внешние условия. Вероятности состояний природы неизвестны и нет возможности получить о них какую-либо статистическую информацию. В качестве оценки каждого решения используется минимальный выигрыш, который можно получить при выборе этого решения:
Лучшим является решение с максимальной оценкой.
Лучшим является решение с максимальной оценкой.
По критерию Вальда выбирают стратегию, которая дает гарантированный выигрыш при наихудшем варианте состояния природы.
Критерий Сэвиджа, как и критерий Вальда, - это критерий крайнего пессимизма, но только пессимизм здесь проявляется в том, что минимизируется максимальная потеря в выигрыше. Для оценки решений используется матрица рисков. В качестве оценки используется максимальный риск (максимальный потерянный выигрыш), соответствующий данному решению:
Лучшим является решение с минимальной оценкой.
Это наиболее осторожный подход к принятию решений и наиболее учитывающий все возможные риски.
Критерий Гурвица:решение принимается с учетом того, что возможны как благоприятные, так и неблагоприятные внешние условия. При использовании этого критерия требуется указать «коэффициент пессимизма» – число в диапазоне от 0 до 1, представляющее собой субъективную (т.е. не рассчитанную, а указанную человеком) оценку возможности неблагоприятных внешних условий. Если есть основания предполагать, что внешние условия будут неблагоприятными, то коэффициент пессимизма назначается близким к единице. Если неблагоприятные внешние условия маловероятны, то используется коэффициент пессимизма, близкий к нулю. Оценки решений находятся по следующей формуле:
где a – коэффициент пессимизма.
Лучшим является решение с максимальной оценкой:
Кроме критериев оптимальности, которые можно применять при принятии решения в условиях риска и неопределенности, существует очень известный и распространенный метод теории игр, используемый в управленческой деятельности в условиях неопределенности.