Линейное программирование

Линейное программирование – наука о методах исследования и отыскание наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения.

Функция, наибольшее и наименьшее значение которой отыскивается, называется целевой функцией.

Построим математические модели простейших экономических задач.

Пример 1 (задача об использовании ресурсов). Для изготовления двух видов продукции Р₁, Р₂ используются три вида ресурсов S₁, S₂, S₃. Запасы ресурсов, затраты ресурсов на единицу продукции, а также цены единицы продукции приведены в следующей таблице

Ресурсы	Затраты ресурсов на ед. продукции		Запасы ресурсов
	Р1	Р2
S1	2	4		2000
S2	4	1		1400
S3	2	1		800
Цена ед. продукции	40	60

Требуется построить план производства, максимизирующий доход.

Построим математическую модель задачи, определив в ней переменные, ограничения и целевую функцию.

Переменные: х₁, х₂ – количество единиц выпускаемой продукции Р₁, Р₂ (объемы производства).

Ограничения. Ограничение на расход ресурсов можно записать в следующем виде

.

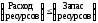Это приводит к следующей системе ограничений:



Кроме того, переменные должны быть неотрицательными.

---

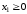
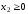, - условие неотрицательности.

Целевая функция – суммарный доход от реализации всей продукции:

, .

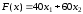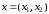Требуется найти такие неотрицательные переменные х₁, х₂, удовлетворяющие ограничениям, при которых суммарный доход максимален, т.е.

.

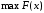Экономико-математическая модель задачи кратко записывается в виде:



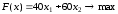
при ограничениях



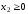, - условие неотрицательности.

Пример 2 (задача составления рациона). Норма пищевого рациона должна содержать не менее b₁, b₂, b₃ питательных веществ S₁, S₂, S₃. Для составления пищевого рациона используются два вида продуктов питания Р₁, Р₂. Содержание питательных веществ в единице каждого продукта и стоимость единицы продукта (цена) приведены в следующей таблице

Питательные Вещества	Содержание питательных веществ в ед. продукта		Норма вещества
	Р1	Р2
S1	3	1	9
S2	1	2	8
S3	1	6	12
Цена ед. продукта	4	6

Требуется так составить пищевой рацион, чтобы обеспечить норму рациона при его минимальной стоимости.

Построим математическую модель задачи, определив в ней переменные, ограничения и целевую функцию.

Переменные: х

---

₁, х₂ – количество единиц соответствующего вида продукта Р₁, Р₂.

Ограничения. Ограничение на содержание питательных веществ в рационе можно записать в следующем виде

.

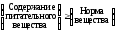Это приводит к следующей системе ограничений:



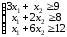
Кроме того, переменные должны быть неотрицательными.

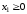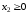, - условие неотрицательности.

Целевая функция – общая стоимость рациона:

, .

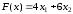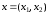Требуется минимизировать стоимость рациона при заданных ограничениях, т.е. .

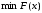Экономико-математическая модель задачи кратко записывается в виде



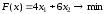
при ограничениях



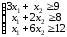
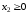, - условие неотрицательности.
Общая задача линейного программирования

Общая задача линейного программирования (ОЗЛП) ставится следующим образом. Найти экстремум (максимум или минимум) линейной целевой функции



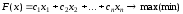
при ограничениях



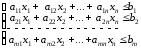
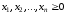- условие неотрицательности,

где x– переменные; a,b,c – заданные постоянные величины.

В системе ограничений неравенства могут быть направлены в ту или иную сторону (, ).

Допустимым решением (планом) ОЗЛП называется вектор x = (x₁, x₂,…, x_n), удовлетворяющий системе ограничений и условию неотрицательности.

Областью допустимых решений (ОДР) называется множество всех допустимых решений ОЗЛП.

Оптимальным решением ОЗЛП называется допустимое решение, при котором целевая функция достигает своего экстремального значения.

---

Геометрическая интерпретация ОЗЛП

Рассмотрим ОЗЛП с двумя переменными (на плоскости).



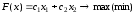
при ограничениях



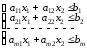
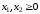- условие неотрицательности.

Свойства решений ОЗЛП тесно связаны со свойствами выпуклых множеств. Рассмотрим на плоскости множество точек .

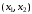Множество точек на плоскости называется выпуклым, если оно вместе с любыми своими двумя точками содержит и весь отрезок, соединяющий их; в противном случае называется невыпуклым.

Примеры выпуклых и невыпуклых множеств показаны на рисунке



Точка А называется внутренней точкой выпуклого множества, если в сколь угодно малой окрестности этой точки содержатся только точки этого множества.

Точка В называется граничной точкой выпуклого множества, если в сколь угодно малой окрестности этой точки содержатся как точки данного множества, так и не принадлежащие ему.

Точка С называется угловой точкой выпуклого множества, если она является граничной и не лежит внутри отрезка, соединяющего две другие точки этого множества.

Множество называется замкнутым, если оно включает все свои граничные точки.

Множество называется ограниченным, если существует окружность радиуса конечной длины с центром в любой точке множества, которое полностью содержит в себе данное множество; в противном случае называется неограниченным.

Пересечением выпуклых множеств называется множество, представляющее общую часть данных множеств.

Свойство: Пересечение выпуклых множеств есть выпуклое множество.

Выпуклым многоугольником называется выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек.

Полуплоскостью называется множество точек на плоскости

---

, координаты которых удовлетворяют неравенству

.

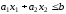Уравнение 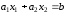является граничной прямой полуплоскости.

Граничная прямая делит плоскость на две полуплоскости. Для определения, на какую сторону от граничной прямой расположена данная полуплоскость, надо взять произвольную точку на плоскости, и подставить координаты этой точки в неравенство. Если неравенство справедливо, то полуплоскость обращена в сторону этой точки, иначе – в противоположную. Направление полуплоскости на рисунках штрихуется.

Полуплоскости являются выпуклыми множествами. Каждое из неравенств системы ограничений определяет полуплоскость. Система ограничений в виде неравенств (пересечение) образует выпуклое множество, которое называется многоугольником решения задачи. Стороны этого многоугольника лежат на граничных прямых, а угловые точки определяются как точки пересечения смежных граничных прямых.

Геометрически задача ЛП представляет отыскание такой точки многоугольника решений, координаты которого доставляют линейной функции F(x) экстремум, причем допустимыми решениями служат все точки многоугольника решений.

Теорема. Если задача ЛП имеет оптимальное решение, то оно достигается в одной из угловых точек многоугольника решений.

Графическое решение задач ЛП. Наиболее простым и наглядным методом ЛП является графический метод. Он применяется для решения задач ЛП с двумя переменными (на плоскости).

Рассмотрим задачу об использовании ресурсов.



при ограничениях



, - условие неотрицательности.

Решим данную задачу графическим методом.

▼ Каждое неравенство системы ограничений определяет полуплоскость с граничной прямой:

L₁: 2x₁ + 4x₂ = 2000;

L₂: 4x₁ + x₂ = 1400;

L₃: 2x₁ + x₂ = 800.

Условие неотрицательности определяют полуплоскости с граничными прямыми x₁ = 0, x

---

Смотрите также файлы

• Слова, обозначающие действия предметов.pptx

• 8 Наурыз Трбие сааты 20222023 оу жылы Таырыбы Ана гл, ана мір шуаы.docx

• Задание Заполнить недостающие показатели таблицы Бухгалтерский баланс.docx

• 1. 2 Общение как основа социальнопедагогической.pdf

• Дисциплина История Практическое занятие 3 Обучающийся Литовченко Любовь Ивановна Преподаватель Новикова Наталья Львовна Задание 1.rtf