Оптимальное решение 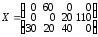, 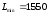усл. ед.

Таким образом, из первого склада следует отправить муку на 2-й хлебозавод в количестве 60 т., из второго склада — на 3-й и 4-й хлебозаводы в количестве 20 и 110 т. со­ответственно, из третьего склада — на 1-й, 2-й и 3-й хлебозаводы в количестве 30, 20 и 40 т. со­ответственно. При этом минимальные транспортные расходы составят 1550 усл. ед ▲

Упражнение 1. На предприятии имеются три группы станков, каждая из которых может выполнять пять операций по обработке деталей (в любом порядке). Максимальное время работы каждой группы станков соответственно равно 100, 250, 180 ч. Каждая операция должна выполняться соответственно 100, 120, 70, 110, 130 ч. Производительность каждой группы станков на каждую операцию задана матрицей 



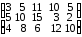
Определить, сколько времени и на какую операцию нужно использовать каждую группу станков, чтобы обработать максимальное количество деталей.

Ответ. Оптимальное решение

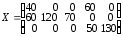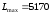, шт.

Таким образом, на первой группе станков целесообразно выполнять операции 1 и 4 продолжительностью 40 и 60 ч со­ответственно, на второй группе — операции 1, 2 и 3 продолжи­тельностью 60, 120 и 70 ч соответственно, на третьей группе — операции 4 и 5 продолжительностью 50 и 130 ч соответственно. При этом максимальное число обработанных деталей составит 5170 шт.

II. Открытая модель, .

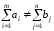Для открытой модели может быть два случая:

a) суммарные запасы превышают суммарные потребности: ;

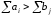b) суммарные потребности превышают суммарные запасы: .

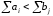В Excel открытая задача решается путем изменения ограничений по предложению (если предложение превышает спрос) или по спросу (если спрос превышает предложение), т.е. система ограничений будет иметь вид:

a) 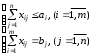- условия неполного распределения запасов и полного удовлетворения потребностей;

b) 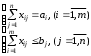- условия полного распределения запасов и неполного удовлетворения потребностей.

---

Пример 1. Три торговых склада могут поставлять некоторое изделие в количестве 9, 4, 8 т. Величина спроса трех магазинов розничной торговли на это изделие равна 3, 5, 6 т соответственно. Стоимости перевозок единицы груза от каждого поставщика к каждому потребителю заданы матрицей



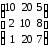
Требуется составить такой план перевозок, при котором спросы на изделия в магазины были бы выполнены при минимальной стоимости всех перевозок.

▼ Рабочий лист Excel и заполненное диалоговое окно Поиск решения имеют вид




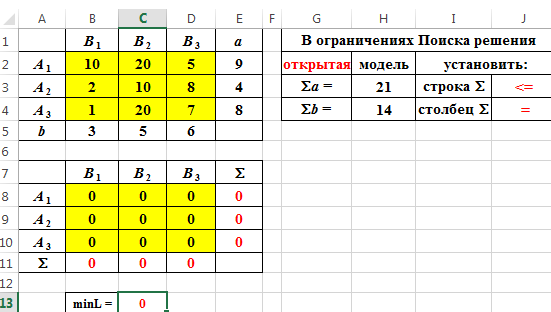
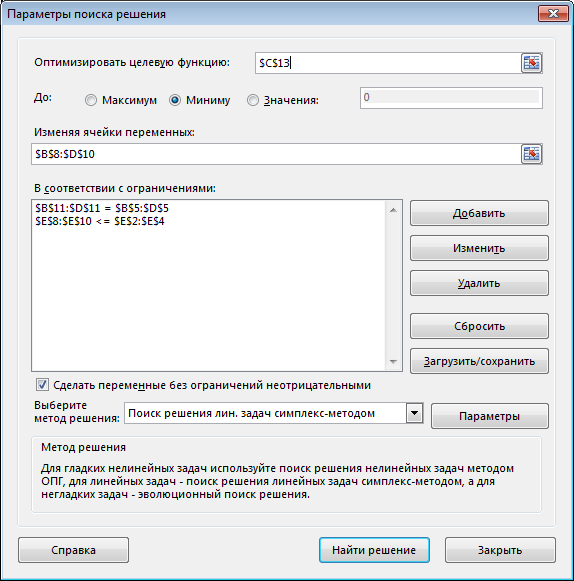
Неравенство $E$8:$E10< = $E$2:$E$4 означает условие неполного распределения запасов.

После выполнения программы работы «Поиск решения» получим

	B1	B2	B3	
А1	0	0	6	6
А2	0	4	0	4
А3	3	1	0	4
	3	5	6
	L =	93

Оптимальное решение

---

, ▲

---

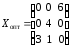
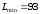Пример 2. Составить оптимальный план перевозки грузов от трех поставщиков с грузами 240, 40, 110 т к четырем потребителям с запросами 90, 190, 40, 130 т. Стоимости перевозок единицы груза от каждого поставщика к каждому потребителю даны матрицей



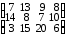
▼ Рабочий лист Excel и заполненное диалоговое окно Поиск решения имеют следующий вид




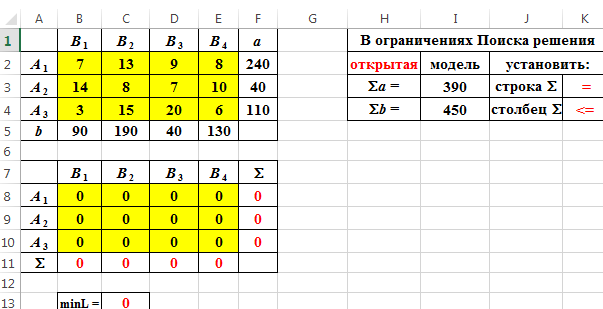
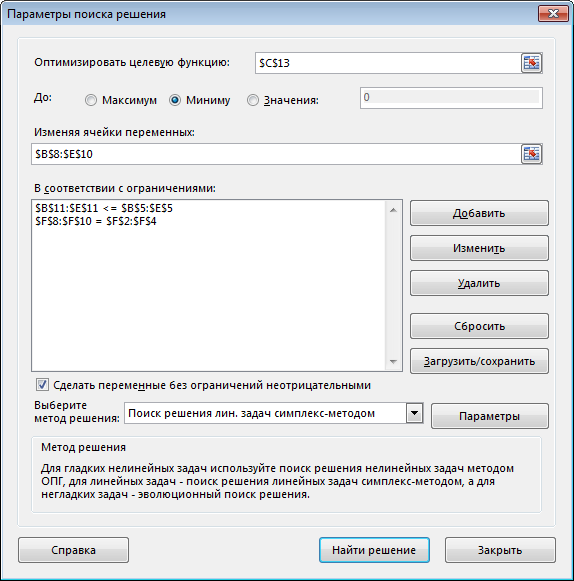
Неравенство $B$11:$E11< = $B$5:$E$5 означает условие неполного удовлетворения потребностей.

После выполнения программы работы «Поиск решения» получим

	B1	B2	B3	B4	
А1	0	90	40	110	240
А2	0	40	0	0	40
А3	90	0	0	20	110
	90	130	40	130
	L =	3120

---

Оптимальное решение , ▲

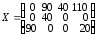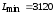Упражнение 1. Три фермерских хозяйства A₁, A₂, A₃ ежедневно могут доставлять в город соответственно 60, 60 и 50 ц молока для обеспечения пяти торговых точек: В₁, В₂, В₃, В₄, В₅. Стоимость перевозки 1 ц молока и потребности торговых точек в молоке указаны в следующей таблице

Фермерские хозяйства	Затраты на перевозку 1 ц к торговым точкам					Запас молока, ц
	B1	B2	B3	B4	B5
А1	7	6	8	10	12	60
А2	9	5	7	4	6	60
А3	6	8	4	9	7	50
Потребности, ц	30	20	55	20	25

Определить оптимальный план поставки молока в каждую точку для удовлетворения потребностей, чтобы суммарные транспортные издержки были минимальными.

Ответ: Оптимальное решение

, .

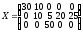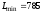Задачи о назначениях

Задача о назначениях имеет место при назначении людей на должности или работы, автомашин на маршруты, водителей на машины и т.п.

В наиболее общей форме задача о назначениях формулируется следующим образом. Имеется некоторое число работ и некоторое число работников. Любой работник может быть назначен на выполнение любой (но только одной) работы, но с неодинаковыми затратами.

---

Смотрите также файлы

• Слова, обозначающие действия предметов.pptx

• 8 Наурыз Трбие сааты 20222023 оу жылы Таырыбы Ана гл, ана мір шуаы.docx

• Задание Заполнить недостающие показатели таблицы Бухгалтерский баланс.docx

• 1. 2 Общение как основа социальнопедагогической.pdf

• Дисциплина История Практическое занятие 3 Обучающийся Литовченко Любовь Ивановна Преподаватель Новикова Наталья Львовна Задание 1.rtf