Файл: Задача об использовании ресурсов. Для изготовления двух видов продукции р 1, р 2 используются три вида ресурсов S.docx
Добавлен: 04.12.2023
Просмотров: 176
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
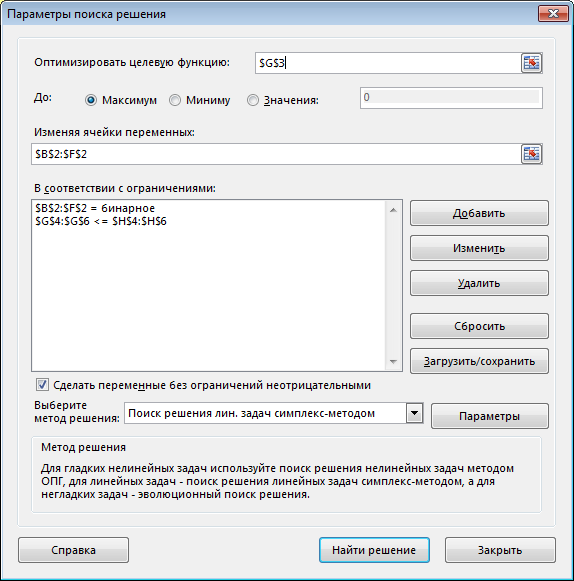
После выполнения программы работы Поиск решения получим
| |  |  |  |  |  | | |
| | 1 | 1 | 0 | 1 | 1 | | |
 | 40 | 60 | 38 | 50 | 55 | 205 | |
 | 12 | 17 | 10 | 7 | 17 | 53 | 54 |
 | 8 | 17 | 7 | 22 | 14 | 61 | 62 |
 | 17 | 20 | 21 | 6 | 20 | 63 | 70 |
Оптимальное решение х = (1; 1; 0; 1; 1), Fmax(x) = 295.
Таким образом, необходимо финансировать 1-й, 2-й, 4-й и 5-й проекты, при этом сумма ЧПС проектов максимальна и составляет 205 усл. ед. Для этого потребуются денежные средства в объеме 53 + 61 + 63 = 177 усл. ед. в течение трех лет при выделенных фирмой 54 + 62 + 70 = 186 ден. ед. ▲
Транспортная задача
Постановка транспортной задачи
Транспортная задача (ТЗ) используется при разработке плана перевозок однородного вида продукции, сосредоточенного в нескольких пунктах отправления в пункты назначения.
Пункты отправления (ПО). Имеется m пунктов отправления A1, A2,…, Am, в которых сосредоточены грузы в количестве a1, a2,…, am ед.
Пункты назначения (ПН). Имеется n пунктов назначения B1, B2,…, Bn, подавшие заявки на b1, b2,…, bn ед. товара.
Известны стоимости (тарифы) cij перевозок единиц товара от каждого ПО в каждый ПН.
Требуется составить такой план перевозок, при котором все заявки на товар были бы выполнены при минимальной стоимости всех перевозок.
В зависимости от соотношения между суммарными запасами груза и суммарными потребностями в нем ТЗ могут быть закрытыми и открытыми.
Если
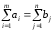, то задача называется закрытой.Если
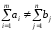, то задача называется открытой.Закрытая транспортная задача
Построим математическую модель задачи, определив в ней переменные, ограничения и целевую функцию.
Переменные: xij - количество груза, отправляемого из пункта Ai в пункт Bj, причем xij 0.
Запишем условия задачи в виде следующей транспортной таблицы
| Транспортная таблица | |||||
| | B1 | B2 | … | Bn | Запасы ai |
| A1 | c11 x11 | c12 x12 | … | c1n x1n | a1 |
| A2 | c21 x21 | c22 x22 | … | c2n x2n | a2 |
| … | … | … | … | … | … |
| Am | cm1 xm1 | cm2 xm2 | … | cmn xmn | am |
| Заявки bj | b1 | b2 | … | bn |  |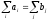
Строки транспортной таблицы соответствуют ПО (в последней клетки каждой строки указан объем запаса груза), а столбцы – ПН (последняя клетка каждого столбца содержит значение потребности. Все клетки таблицы (кроме тех, которые расположены в нижней строке и в правом столбце) содержат информацию о перевозках xij и их стоимости сij.
Запишем систему ограничений.
1) Ограничение по уровню запасов: Суммарное количество груза, направленного из каждого ПО во все ПН должно быть равно запасу груза в данном ПО:
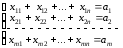
2) Ограничение по уровню спроса: Суммарное количество груза, доставляемого в каждый ПН из всех ПО должно быть равно заявке данного ПН:
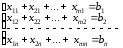
Целевая функция: Суммарная стоимость всех перевозок, которую необходимо минимизировать:
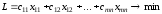
Планом перевозок называется любая совокупность значений переменных xij - матрица размера m×n.
Допустимым решением называется план xij, удовлетворяющий системе ограничений ТЗ.
Оптимальным решением называется допустимое решение, доставляющее минимум целевой функции.
Решение ТЗ в Excel
Надстройка Поиск решения в Microsoft Excel позволяет напрямую находить оптимальное решение транспортной задачи.
I. Закрытая модель,
.До вызова Поиск решения необходимо подготовить данные для решения ТЗ на рабочем листе Excel.
В Excel закрытая задача решается учетом ограничений для всех отправителей и всех потребителей
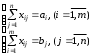- условия полного распределения запасов и полного удовлетворения потребностей.Пример 1. На трех складах имеется мука в количестве 60, 130, 90 т., которая должна быть доставлена четырем хлебозаводам в количестве 30, 80, 60, 110 т соответственно. Составить оптимальный план перевозок, имеющий минимальные транспортные расходы, если стоимость доставки 1 т муки на хлебозаводы задана матрицей
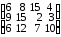
▼ Рабочий лист
Excel для примера 2.30
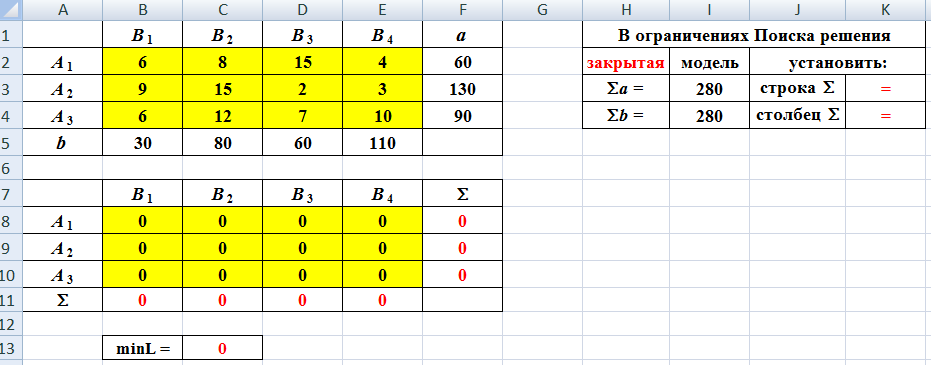
В правой части табл. 2.30 указана подсказка:
Приведем последовательность ввода данных задачи и формул в соответствующие ячейки.
A1:F5 — вводится транспортная таблица примера.
I3 — вычисляется сумма по строкам по формуле: =СУММ(F2:F4).
I4 — вычисляется сумма по столбцам по формуле: =СУММ(B5:E5).
Из сравнения значений делается сообщение о типе модели (закрытая, открытая) и типе ограничений (=, < =) в окне Поиск решения.
A7:F11 — составляется начальная матрица перевозок (вначале копируется транспортная таблица, затем редактируется)
В8:Е10 — производится резервирование и обнуление изменяемых переменных (начальная матрица перевозок).
F8:F10 и B11:E11 — подсчитываются суммы Σ по строкам и столбцам начальной матрицы перевозок.
С13 — вычисляется стоимость начального плана L по формуле: =СУММПРОИЗВ(B2:E4;B8:E10).
Далее нужно выполнить команду Поиск решения. В диалоговом окне Поиск решения:
• установить целевую ячейку L равной минимальному значению;
• в качестве изменяемых ячеек ввести матрицу перевозок xij;
• установить ограничение для всех отправителей и всех потребителей;
• выбрать метод решения: Поиск решения лин. задач симплекс-методом.
Заполненное диалоговое окно Поиск решения имеет следующий вид
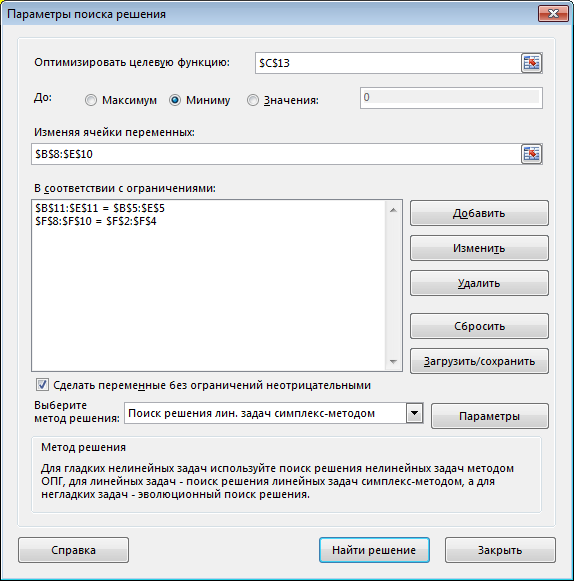
Равенство $B$11:$E$11 = $B$5:$E$5 означает условие полного удовлетворения потребностей.
Равенство $F$8:$F$10 = $F$2:$F$4 означает условие полного распределения запасов.
После выполнения программы работы «Поиск решения» получим
| | B1 | B2 | B3 | B4 | |
| А1 | 0 | 60 | 0 | 0 | 60 |
| А2 | 0 | 0 | 20 | 110 | 130 |
| А3 | 30 | 20 | 40 | 0 | 90 |
| | 30 | 80 | 60 | 110 | |
| | | | | | |
| | L = | 1550 | | | |