ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 35
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Псковский государственный университет»
Финансово-экономический факультет
Кафедра экономики и финансов
Расчётно-контрольная работа
«Финансовые вычисления»
Вариант 9
Студент: Соколова Т.А.
Группа: 0073-05
Руководитель: Федорова Н.Ю.
Псков
2014
-
Задача 1. На банковском вкладе проценты начисляются на основе сложной «плавающей» ставки, которая изменяется каждый год. Три года назад на счет положили 10000 руб., когда процентная ставка была 13%. В прошлом году она упала до 6%, а в этом году установлена на уровне 16%. Какая сумма будет на счете к концу текущего года? -
Дано: -
PV = 10000 руб. -
i1 = 13% -
i2 = 6% -
i3 = 16% -
n = 3 года -
Найти: -
FV -
Решение -
Для определения наращённой суммы в конце текущего года воспользуемся формулой определения будущей стоимости с переменной ставкой процента: -
FV = PV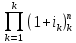 = PV* (1+ i1)n1(1+ i2)n2*…*
= PV* (1+ i1)n1(1+ i2)n2*…*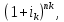 где
где -
FV – наращённая (будущая) стоимость вклада; -
PV – первоначальная сумма вклада; -
i1, i2 … iK – ставка процента в каждом периоде; -
n1, n2…nk - продолжительность каждого периода в годах, тогда -
FV = 10000*(1+0,13)*(1+0,06)*(1+0,16) = 13894,48 руб. -
Ответ: По истечению 3-х лет сумма на счёте в банке составит 13894,48 руб. -
Задача 2. На депозитный счёт в банке сделан вклад в сумме 10000 руб. под 6 годовых на срок 16 лет. Какая часть дохода от вложения обеспечена применением сложного начисления процентов по сравнению с простым.
Сумма вклада 10000 руб. Срок вклада 16 лет. Процентная ставка 6 % годовых. Какая часть дохода от вложения обеспечивается применением сложного начисления процентов по сравнению с простым.
Решение
FV = 10000*1.0616 = 25403,5 руб.
I = FV – PV =25403,5 – 10000 = 15403,5 руб., следовательно,
Доход от применения сложной процентной ставки по сравнению с простой =
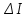 = Iслож – Iпрост = 15403,5 -9600 = 5803,5 руб.
= Iслож – Iпрост = 15403,5 -9600 = 5803,5 руб.Часть дохода от вложения, обеспечивающая применением сложного начисления процентов по сравнению с простым =
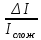 *100% =
*100% =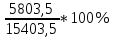 = 37,7%
= 37,7% -
Задача 3. В банке получен кредит на сумму 10000 тыс. руб. для приобретения квартиры при условии погашения его равными ежегодными платежами. Срок погашения кредита составляет 16 лет, а процентная ставка равна 6% годовых. Необходимо рассчитать размер ежегодного платежа и составить график погашения кредита. Данные для расчёта представлены в задаче 1. График погашения кредита представляется в виде таблице. -
В банке взят кредит на сумму 10000 тыс. руб. с целью приобретения квартиры, при условии погашения его равными ежегодными платежами. Срок погашения кредита составляет 16 лет, а процентная ставка 6 % годовых. Рассчитать размер ежегодного платежа и составить график погашения кредита. -
Решение -
А =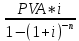 ,
, -
A=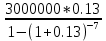 = 678332.41 руб. в год.
= 678332.41 руб. в год. -
2. График погашения займов предоставлен в таблице 1 -
Таблица 1 -
График погашения займа -
| Год | Начальный долг | Общий платеж | Выплаченные проценты | Выплаченная основная сумма долга | Остаток долга |
| 1 | 10000000 | 989521,43589 | 600000 | 389521,43589 | 9610478,56411 |
| 2 | 9610478,56411 | 989521,43589 | 576628,71385 | 412892,72204 | 9197585,84207 |
| 3 | 9197585,84207 | 989521,43589 | 551855,15052 | 437666,28537 | 8759919,5567 |
| 4 | 8759919,5567 | 989521,43589 | 525595,1734 | 463926,26249 | 8295993,29421 |
| 5 | 8295993,29421 | 989521,43589 | 497759,59765 | 491761,83824 | 7804231,4559 |
| 6 | 7804231,45597 | 989521,43589 | 468253,88736 | 521267,54853 | 7282963,90744 |
| 7 | 7282963,90744 | 989521,43589 | 436977,83445 | 552543,60144 | 6730420,306 |
| 8 | 6730420,306 | 989521,43589 | 403825,21836 | 585696,21753 | 6144724,08847 |
| 9 | 6144724,08847 | 989521,43589 | 368683,44531 | 620837,99058 | 5523886,09789 |
| 10 | 5523886,09789 | 989521,43589 | 331433,16587 | 658088,27002 | 4865797,82787 |
| 11 | 4865797,82787 | 989521,43589 | 291947,86967 | 697573,56622 | 4168224,26165 |
| 12 | 4168224,26165 | 989521,43589 | 250093,4557 | 739427,98019 | 3428796,28146 |
| 13 | 3428796,28146 | 989521,43589 | 205727,77689 | 783793,659 | 2645002,62246 |
| 14 | 2645002,62246 | 989521,43589 | 158700,15735 | 830821,27854 | 1814181,34392 |
| 15 | 1814181,34392 | 989521,43589 | 108850,88064 | 880670,55525 | 933510,78867 |
| 16 | 933510,7886 | 989521,43589 | 560010,64732 | 933510,7887 | 0 |
-
Задача 4. Вы выиграли приз в лотерее. Имеется два варианта получения приза. По первому вы получаете 55000 $ через год, а по второму 30000 $ сразу, и по 1000 $ в конце каждого года в течение последующих 30 лет. Какой вариант является более предпочтительным, если процентная ставка равна З %. -
В лотерею был выигран приз, который можно получить двумя способами: -
1 способ: Получение приза в сумме 55000 долл. через год -
2 способ: Получение 30000 долл. сразу и 1000 долл. в конце каждого года в последующие 30 лет. -
Какой способ предпочтительней (для того кто выиграл), если процентная ставка 3 % годовых. -
Решение: -
1 случай -
PV =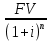 =
= 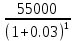 = 53398,06 долл.
= 53398,06 долл. -
2 случай -
PVA = R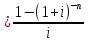 = 1000
= 1000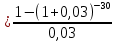 = 19600,33 долл.
= 19600,33 долл. -
Учитывая, что 2-й случай предполагает первый платёж = 30000 долл., то -
PV = 49600,33 долл., следовательно 1 случай получения приза является более предпочтительным, т.к. сумма больше. -
-
Задача 5. Вы планируете приобрести квартиру через 3 года. Эксперты оценивают будущую стоимость недвижимости в размере 1 млн. рублей. По банковским депозитным счетам установлены ставки в размере 13% с ежеквартальным начислением процентов. Определить, какую сумму средств необходимо поместить на банковский депозитный счет, чтобы через 3 года получить необходимую для приобретения квартиры сумму. -
Решение -
PV =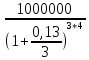 = 601091,58 руб
= 601091,58 руб -
Ответ: -
-
Задача 6. Вы в возрасте 38 лет положили на счет 30000 долл. с тем, чтобы снять их со счета не раньше, чем вам исполнится 60 лет. Какая сумма будет у вас на счете, если процентная ставка составляет 13 %, а уровень инфляции – 9 %. Какова будет реальная стоимость ваших накоплений?
-
Решение -
FVреал. = PV* (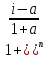 = 30000*(1+
= 30000*(1+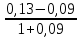 )22 = 66296,4 долл.
)22 = 66296,4 долл. -
-
Задача 7. Вам осталось 38 лет до пенсии, и вы надеетесь прожить еще 15 лет после выхода на пенсию. Если вы начнете откладывать деньги начиная с текущего года, то каков будет размер ежегодных номинальных и реальных пенсионных выплат на каждый рубль ежегодных инвестиций при годовой процентной ставке 13 % и уровне инфляции 9 %.
-
9Решение: -
FVA= R*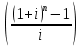 , где
, где -
R = , где
, где -
1 случай (если используется номинальная процентная ставка) -
FVA= R*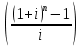 = 1*
= 1*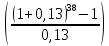 = 792,21 руб.
= 792,21 руб. -
FVA = PVA = 792,21 руб. -
R = =
= 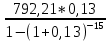 =
= 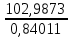 =122,59 руб.
=122,59 руб. -
2 случай (если используется реальная процентная ставка) -
FVA= R*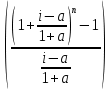 = 1*
= 1*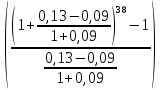 =
= 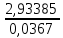 = 79,94 руб.
= 79,94 руб. -
FVA = PVA = 79,94 руб. -
R =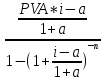 =
= 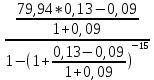
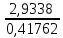 = 7,03 руб.
= 7,03 руб. -
-
Задача 8. У вас есть возможность участвовать в инвестиционном проекте, который обеспечит поступление в конце первого года 25000 руб., в конце следующего – 20000 руб., а в конце третьего, последнего года вам требуется уплатить 48000 руб. Оцените целесообразность такого участия, если ставка дисконтирования составляет 9 %.
-
Решение -
PV =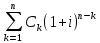 = 25000
= 25000  + 20000
+ 20000 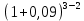 = 29702,5+21800=51502,5 руб.
= 29702,5+21800=51502,5 руб. -
NPV = PV – IC = 51502,5 – 48000 = 3502,5 руб. -
-
Задача 9. Инвестор предполагает приобрести облигацию номиналом 10000 руб, по которой выплачивается 13 процентов годовых. Выплата процентов производится один раз в год. До погашения облигации остается 6 лет. Требуемая норма прибыли в течение первых трех лет – 20%, четвертый год – пятый год – 15%, 6 год и т.д. – 10 %. Определить курсовую цену облигации, а также доходность к погашению.
-
Решение -
К.Ц. =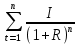 +
+ 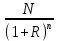 =
= -
(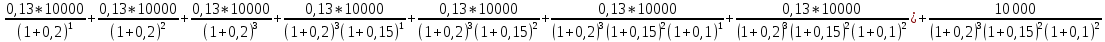 = 8565,13 руб.
= 8565,13 руб. -
R =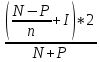 =
= 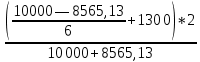 *100% = 16,58%
*100% = 16,58% -
-
Задача 10. На фондовом рынке продаются акции акционерного общества «Альфа». Ожидаемые дивиденды в течение первых 3 лет составляют 70 руб. на акцию. В последующие годы прогнозируются темпы прироста дивидендов – 14 % в год. Требуемая норма прибыли на акцию – 19 % годовых. Определить цену акции, если инвестор собирается держать акцию неограниченно долго. -
Решение -
P = D*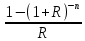 +
+ 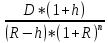 = 70*
= 70*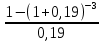 +
+ 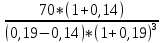 = 70*
= 70*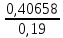 +
+ 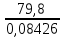 = 149,79+947,07 = 1096,86 руб.
= 149,79+947,07 = 1096,86 руб. -