Министерство образования и науки Российской Федерации

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРОМЫШЛЕННЫХ ТЕХНОЛОГИЙ И ДИЗАЙНА»


Кафедра экономики и финансов

Контрольная работа
по дисциплине

«Методы принятия управленческих решений».

Исполнитель:

студентка группы 3-ЭЗП-20

Майорова К.А.

Санкт-Петербург

2023
Вариант 5.

Задание 1.

1) считая что у₁-у₄ – возможные состояния внешней среды, найти оптимальное решение при Р(у₁) = 0,3; Р(у₂) = 0,2; Р(у₃) = 0,4; Р(у₄) = 0,1.

2) решить задачу при неизвестных вероятностях состояний, используя критерий Вальда, крайнего оптимизма и Гурвица при К = 0,5.

3) считая, что у₁-у₄ – возможные стратегии второго игрока, найти оптимальные стратегии игроков при заданной платежной матрице Q.

xi/yi	y1	y2	y3	y4
x1	3	-12	20	1
x2	2	-15	17	8
x3	6	-10	3	5
x4	-2	-5	-2	-1

Решение.

1) За оптимальные принимается та стратегия (чистая) A_i, при которой максимизируется средний выигрыш a или минимизируется средний риск r. Считаем значения ∑(х_ijp_j)

∑(х_1,jp_j) = 3·0,3 + (-12)·0,2 + 20·0,4 + 1·0,1 = 6,6

∑(х_2,jp_j) = 2·0,3 + (-15)·0,2 + 17·0,4 + 8·0,1 = 5,2

∑(х_3,jp_j) = 6·0,3 + (-10)·0,2 + 3·0,4 + 5·0,1 = 1,5

∑(х_4,jp_j) = (-2)·0,3 + (-5)·0,2 + (-2)·0,4 + (-1)·0,1 = -2,5

хi	y1	y2	y3	y4	∑(хijpj)
х1	0,9	-2,4	8	0,1	6,6
х2	0,6	-3	6,8	0,8	5,2
х3	1,8	-2	1,2	0,5	1,5
х4	-0,6	-1	-0,8	-0,1	-2,5
pj	0,3	0,2	0,4	0,1

---

Выбираем из (6,6; 5,2; 1,5; -2,5) max = 6,6. Ответ: Выбираем стратегию N=1.

2) По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е. a = max(min a_ij)

хi	y1	y2	y3	y4	min(хij)
х1	3	-12	20	1	-12
х2	2	-15	17	8	-15
х3	6	-10	3	5	-10
х4	-2	-5	-2	-1	-5

Выбираем из (-12; -15; -10; -5) максимальный элемент max = -5. Ответ: выбираем стратегию N = 4.

Критерий крайнего оптимизма (критерий максимакса) ориентирует статистику на самые благоприятные состояния природы, т.е. этот критерий выражает оптимистическую оценку ситуации.

xi	y1	y2	y3	y4	max(хij)
x1	3	-12	20	1	20
x2	2	-15	17	8	17
x3	6	-10	3	5	6
x4	-2	-5	-2	-1	-1

---

Выбираем из (20; 17; 6; -1) максимальный элемент max = 20.

Ответ: выбираем стратегию N = 1.

Критерий Гурвица является критерием пессимизма - оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение: max(s_i),

где s_i = К min(x_ij) + (1 – К)max(x_ij) Рассчитываем s_i.

s₁ = 0,5·(-12) + (1 – 0,5)·20 = 4

s₂ = 0,5·(-15) + (1 – 0,5)·17 = 1

s₃ = 0,5·(-10) + (1 – 0,5)·6 = -2

s₄ = 0,5·(-5) + (1 – 0,5)·(-1) = -3

xi	y1	y2	y3	y4	min(xij)	max(xij)	К·min(xij) + (1 – К)·max(xij)
x1	3	-12	20	1	-12	20	4
x2	2	-15	17	8	-15	17	1
x3	6	-10	3	5	-10	6	-2
x4	-2	-5	-2	-1	-5	-1	-3

Выбираем из (4; 1; -2; -3) максимальный элемент max = 4. ответ: выбираем стратегию N = 1. Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A₁.

3) считая, что у₁-у₄ – возможные стратегии второго игрока, найти оптимальные стратегии игроков при заданной платежной матрице Q.

Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях. Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.

---

Игроки	y1	y2	y3	y4	a = min(хi)
х1	3	-12	20	1	-12
х2	2	-15	17	8	-15
х3	6	-10	3	5	-10
х4	-2	-5	-2	-1	-5
b = max(уi)	6	-5	20	8

Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(х_i) = -5, которая указывает на максимальную чистую стратегию A₄. Верхняя цена игры b = min(у_j) = -5. Седловая точка (4, 2) указывает решение на пару альтернатив (х₄, у₂). Цена игры равна -5.

Задание 2.

Потребность сборочного предприятия в деталях некоторого типа составляет D = 11 500 деталей в год, причем эти детали расходуются в процессе производства равномерно. Детали поставляются партиями равного объема. Хранение детали на складе стоит c_h = 150 рублей в год, а поставка партии с₀ = 11 000 рублей. Определить наиболее экономичный объем партии и интервал между поставками.

Решение. Оптимальную величину заказа определим по формуле:



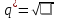
Оптимальное количество заказов в год:



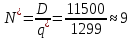
Оптимальное время между заказами:

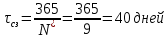
Задание 3.

Заявки поступают по телефону с интенсивностью λ = 115 (1/ч), а средняя продолжительность разговора по телефону

---

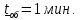
Определите финальные вероятности состояний системы и показатели эффективности работы СМО (вероятность отказа, относительную и абсолютную пропускную способность) при наличии одного телефонного канала.

Решение.

Интенсивность потока обслуживаний:



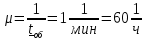
Финальные вероятности состояний системы:





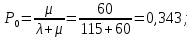
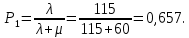
Относительная пропускная способность:



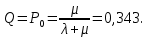
Вероятность отказа:



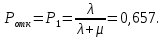
Абсолютная пропускная способность:



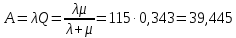
т.е. в среднем в час будут обслужены 39,5 заявок. Очевидно, что при наличии только одного телефонного номера СМО будет плохо справляться с потоком заявок.

Задание 4.

Решить задачу предыдущего задания при наличии трех телефонных каналов (найти финальные вероятности состояний и характеристики эффективности работы СМО).

Решение.

по условию n = 3; λ = 115 (1/ч);

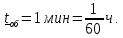
Интенсивность потока обслуживаний:



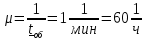
Интенсивность нагрузки телефонного канала:



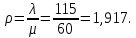
Найдем предельные вероятности состояний:







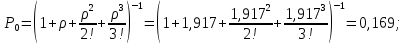
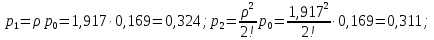
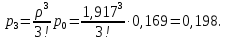
Вероятность отказа (вероятность того, что все 3 телефонных канала будут заняты):

---

Смотрите также файлы

• По каким признакам можно понять, будет ли человек получать удовлетворение от работы в качестве менеджера или нет.docx

• Методические рекомендации по выполнению рейтинговой (контрольной) работы по дисциплине Административное право.docx

• Повседневная жизнь средневекового города в Европе и Древней Руси.pdf

• Продолжение вопроса 1.pdf

• 21ЗБ11 Чернецкая Мария.docx