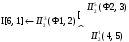ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Структурное исследование плоских рычажных механизмов
Задание 16-а. Произвести структурное исследование механизма (рис.1.1).Рис. 1.1Решение.Степень подвижности механизма определим по формуле Чебышева П.Л.:W=3n-2P5-P4;здесь n =5 - число подвижных звеньев;P5 = 7 – число кинематических пар пятого класса; P4 = 0 - число кинематических пар четвертого класса (высших пар).После подстановки получимW=3·5-2·7-0=1Таким образом, положение механизма полностью характеризуется заданием положения одного любого звена, образующего кинематическую пару со стойкой.Механизм не имеет местных подвижностей и высших кинематических пар.Очевидно, что исследуемый механизм может иметь одно начальное звено из множества – 1, 4 или 5.Если 1 звено принять за начальное, то в состав механизма входят структурная группа 3-го класса 3-го порядка (рис. 1. 2, а) и начальный механизм первого класса (рис. 1.2, б).а) б)Рис. 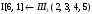1.2Класс механизма равен трем и соответствует наивысшему классу группы Ассура в его составе.Формула строения механизма:Задание 16-б. Произвести структурное исследование механизма (рис. 1.3).Рис. 1.3Решение.Степень подвижности механизма определим по формуле Чебышева П.Л.:W=3n-2P5-P4;здесь n = 5 - число подвижных звеньев;P5 = 6 – число кинематических пар пятого класса; P4 = 2 - число кинематических пар четвертого класса (высших пар).После подстановки получимW=3·5-2·6-2=1Таким образом, положение механизма полностью характеризуется заданием положения одного любого звена, образующего кинематическую пару со стойкой.Произведем замену каждой высшей кинематической пары двумя парами пятого класса и фиктивным звеном (рис. 1.4).
Рис. 1.4В результате замены высших пар получаем мгновенно - заменяющий механизм с той же подвижностью, что и до замены; поскольку n = 7, P4 = 0, P5 = 10, то, следовательноW=3·7-2·10-0=1.Очевидно, что исследуемый механизм может иметь только одно начальное звено из множества – 1, 2, 3 или 5.Если 1 звено принять за начальное, то в состав механизма входят: структурная группа 2-го класса 2-го порядка 1 вида (рис. 1.5, а), структурная группа 2-го класса 2-го порядка 5 вида (рис. 1.5, б), структурная группа 2-го класса 2-го порядка 3 вида (рис. 1.5, в) и начальный механизм первого класса (рис. 1.5, г).а) б) в) г) Рис. 1.5Класс механизма равен двум и соответствует наивысшему классу группы Ассура в его составе.Формула строения механизма:
