Добавлен: 04.12.2023
Просмотров: 24
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ
ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ ВТОРОГО ПОРЯДКА
Данная работа подводит итог изучения переходных режимов в электрических цепях и усвоения методов их анализа. Для расчета переходного процесса предлагается цепь второго порядка, в которой действуют два источника постоянных воздействий.
Предполагается, что до срабатывания коммутаторов (коммутатор работает на замыкание) цепь находилась в установившемся режиме.
Задача расчета переходных процессов сводится к решению системы дифференциальных уравнений, связывающих заданные воздействия и искомые токи и напряжения в исследуемой послекоммутационной цепи. Сформулированная задача может быть решена на основе классической теории дифференциальных уравнений (классический метод), операционного исчисления (операторный метод), численных методов (метод пространства состояний).
2.1. Задание
1. На откидном листе изобразить электрическую цепь, подлежащую расчету, привести численные значения параметров и задающих источников тока и напряжения.
2. Рассчитать указанный преподавателем ток или напряжение в одной из ветвей классическим методом.
3. Составить эквивалентную операторную схему и записать для нее систему уравнений по законам Кирхгофа. Рассчитать искомый ток операторным методом.
4. Построить графики изменения во времени найденных величин.
2.2. Выбор варианта
1. Расчетная цепь выбирается в соответствии с номером варианта с помощью табл. 2.1. Графы расчетных цепей изображены на рис. 2.1.
2. Параметры пассивных элементов цепи и задающих источников цепей во всех вариантах определяются следующим образом:
L = 0,5М Гн , С = 100N мкФ;
величина сопротивлений для четных ветвей R = 100Аr Ом,
для нечетных ветвей R = 20(Аr + N)Ом;
параметры источников: Е1 = 20 (N + M) В, Е2= 20N B, J = 0,1 (N + 2M) А,
где N – номер группы (для студентов заочного отделения: 1 – для студентов, обучающихся в нормативные сроки, 2 – для студентов, обучающихся в сокращенные сроки);
M – шифр специальности, для АТ – 1; АСУ – 2; ЭС – 1,5; ТК – 2,5; КТЭИ – 3; АЭП (АТПП) – 3,5; АТП – 4; АУЦ – 4,5; ЭВТ – 5; КРЭС – 5,5; КЗИ – 6; КСК – 6,5; ИВК – 2;
Ar–сумма цифр номера варианта.
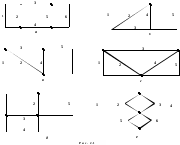
Таблица 2.1
| Вариант | Граф | Ключ | Расположение элементов в ветвях цепи | |||||
| E1 | Е2 | J | R | L | C | |||
| 1, 26, 51, 76 | а | 3 | 1 | – | 6 | 1, 5, 4 | 3 | 2 |
| 2, 27, 52, 77 | б | 5 | 1 | 5 | – | 3, 4, 5 | 1 | 2 |
| 3, 28, 53, 78 | в | 2 | 3 | – | 5 | 1, 2, 3 | 3 | 4 |
| 4, 29, 54, 79 | г | 3 | 1 | – | 5 | 1, 4, 3 | 1 | 2 |
| 5, 30, 55, 80 | д | 4 | 1 | 5 | – | 2, 4, 5 | 1 | 3 |
| 6, 31, 56, 81 | е | 4 | 1 | 4 | – | 1, 3, 4, 5, 6 | 5 | 2 |
| 7, 32, 57, 82 | а | 6 | 6 | – | 1 | 2, 3, 5, 6 | 2 | 5 |
| 8, 33, 58, 83 | б | 2 | 5 | 3 | – | 1, 2, 3, 5 | 4 | 1 |
| 9, 34, 59, 84 | в | 2 | 1 | – | 4 | 1, 4, 5 | 2 | 5 |
| 10 , 35, 60, 85 | г | 4 | 3 | 1 | – | 2, 3, 4, 5 | 5 | 1 |
| 11, 36, 61, 86 | д | 4 | 1 | 4 | – | 1, 2, 3, 4, 5 | 1 | 2 |
| 12, 37, 62, 87 | е | 6 | 4 | – | 2 | 3, 4, 5, 6 | 4 | 1 |
| 13,38,63, 88 | а | 4 | 1 | – | 6 | 1, 4, 5 | 3 | 2 |
| 14, 39, 64, 89 | б | 4 | 4 | – | 5 | 1, 4, 3 | 1 | 2 |
| 15, 40, 65, 90 | в | 5 | 4 | 5 | – | 1, 3, 4, 5 | 1 | 2 |
| 16, 41, 66, 91 | г | 5 | 5 | – | 2 | 1, 3, 4, 5 | 4 | 1 |
| 17, 42, 67, 92 | д | 4 | 1 | 4 | – | 1, 3, 4, 5 | 5 | 2 |
| 18, 43, 68, 93 | е | 2 | 3 | – | 1 | 2, 3, 4, 6 | 5 | 3 |
| 19, 44, 69, 94 | а | 6 | 2 | 5 | – | 1, 5, 6 | 1 | 2 |
| 20, 45, 70, 95 | б | 5 | 3 | 5 | – | 2, 4, 5 | 4 | 1 |
| 21, 46, 71, 96 | в | 2 | 4 | – | 5 | 1, 2, 3, 4 | 1 | 3 |
| 22, 47, 72, 97 | г | 5 | 3 | – | 1 | 2, 3, 5 | 3 | 4 |
| 23, 48, 73, 98 | д | 4 | 1 | – | 2 | 1, 3, 4 | 3 | 5 |
| 24, 49, 74, 99 | е | 1 | 6 | – | 4 | 1, 2, 3, 6 | 3 | 5 |
| 25, 50, 75, 100 | а | 5 | 3 | – | 2 | 1, 3, 5, 6 | 1 | 4 |
Выбор искомой величины
| № варианта | искомая величина | № варианта | искомая величина | № варианта | искомая величина | № варианта | искомая величина |
| 1 | I1 | 26 | I4 | 51 | I5 | 76 | IC |
| 2 | I4 | 27 | I5 | 52 | IC | 77 | I3 |
| 3 | I2 | 28 | I1 | 53 | IC | 78 | UL |
| 4 | I4 | 29 | I3 | 54 | IC | 79 | UL |
| 5 | I2 | 30 | I4 | 55 | I5 | 80 | IC |
| 6 | I4 | 31 | I1 | 56 | I5 | 81 | I3 |
| 7 | IC | 32 | I3 | 57 | I6 | 82 | UL |
| 8 | I3 | 33 | IC | 58 | I2 | 83 | I5 |
| 9 | I1 | 34 | IC | 59 | UL | 84 | UR1 |
| 10 | I4 | 35 | IC | 60 | I3 | 85 | I2 |
| 11 | I5 | 36 | IC | 61 | I4 | 86 | I3 |
| 12 | I5 | 37 | IC | 62 | UL | 87 | I3 |
| 13 | I4 | 38 | I5 | 63 | IC | 88 | I1 |
| 14 | I3 | 39 | I4 | 64 | UL | 89 | IC |
| 15 | I3 | 40 | I5 | 65 | UL | 90 | I4 |
| 16 | I3 | 41 | IC | 66 | I5 | 91 | UL |
| 17 | I3 | 42 | I4 | 67 | I1 | 92 | IC |
| 18 | I6 | 43 | I2 | 68 | I4 | 93 | IC |
| 19 | I5 | 44 | I6 | 69 | IC | 94 | UL |
| 20 | I2 | 45 | I5 | 70 | IC | 95 | I3 |
| 21 | IC | 46 | I4 | 71 | I2 | 96 | UL |
| 22 | I5 | 47 | I2 | 72 | I2 | 97 | IC |
| 23 | I4 | 48 | I1 | 73 | IC | 98 | UL |
| 24 | I1 | 49 | I2 | 74 | IC | 99 | I6 |
| 25 | I6 | 50 | I5 | 75 | I3 | 100 | IC |
2.3. Методические указания
2.3.1. Классический метод расчета
Переходный процесс можно рассчитать классическим методом в следующей последовательности:
1.Расчет докоммутационного установившегося режима с целью получения независимых начальных условий (правил коммутации):
iL(0–) = iL(0+), uC(0–) = uC(0+).
2.Составление характеристического уравнения цепи и определение его корней.
3.Запись полного решения в виде суммы принужденной и свободной составляющих.
4.Расчет послекоммутационного установившегося режима с целью получения принужденных составляющих.
5.Расчет необходимых начальных условий (значение искомой величины и ее производной в момент t = 0+) с использованием уравнений Кирхгофа и независимых начальных условий или схем замещения в момент t = 0+.
6.Определение постоянных интегрирования и функции, описывающей изменение искомой величины в переходном режиме.
2.3.2. Операторный метод расчета
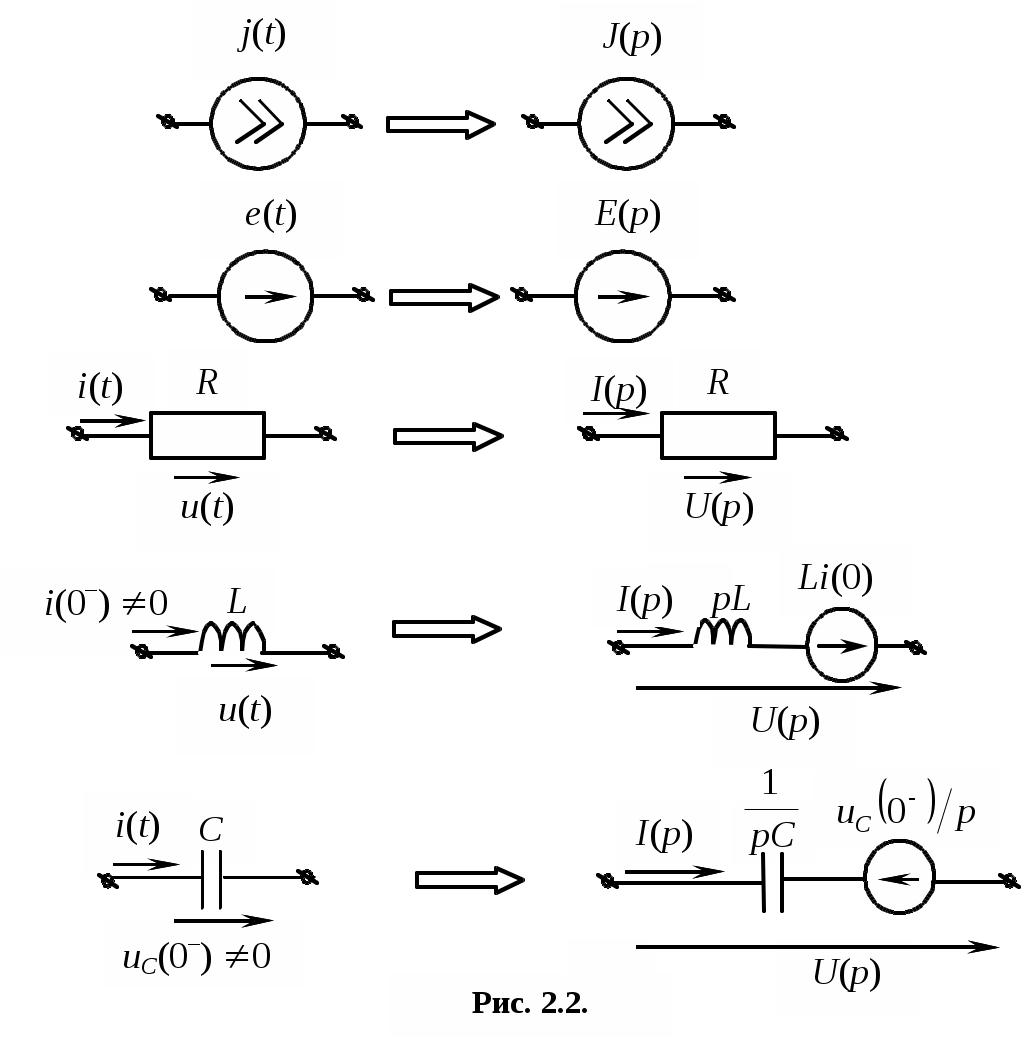
При расчете переходных процессов операторным методом удобно составить предварительно операторную схему. В каждой ветви с параметрами R, L, Cдолжны быть при ненулевых начальных условиях учтены две дополнительные внутренние ЭДС Li(0) и uC(0)/p. На рис. 2.2 показаны переходы от элементов с мгновенными значениями токов и напряжений к элементам операторной схемы.
Далее для операторной схемы замещения составляется система уравнений Кирхгофа в операторной форме, или ведется расчет любым другим известным расчетным методом. В результате решения должно быть получено изображение по Лапласу искомой величины, которому с применением теоремы разложения(таблиц, связывающих оригиналы и их изображения или при помощи других методов) ставится в соответствие оригинал в виде функции времени.
Порядок расчета переходных процессов операторным методом
1. Анализ независимых начальных условий (для этого необходимо рассчитать режим в t=0–).
2. Составление эквивалентной операторной схемы.
3. Расчет операторной схемы любым расчетным методом в операторной форме, преобразование изображения X(p
) искомой величины к виду рациональной дроби.
4. Определение оригинала x(t) по X(p), т.е. обратный переход.
Определение оригинала x(t) по изображению X(p)
Оригинал можно определить описанными ниже способами.
-
Использование обратного преобразования Лапласа
, (2.1)которое представляет собой решение интегрального уравнения относительно неизвестной функции f(t) и может быть получено методами теории функций комплексного переменного. Интеграл (2.1) вычисляется по прямой на плоскости комплексного переменного p, параллельной мнимой оси и расположенной правее всех особенностей (в частности, простых и кратных полюсов) функции F(p). Такой способ в прикладных задачах электротехники не используется.
2. Табличный метод. Подробные таблицы оригиналов и соответствующих им изображений приводятся в математических и электротехнических справочниках. При использовании этого способа возникают трудности, связанные с распознаванием и сведением функций к табличному виду.
3. Использование теоремы о вычетах или теоремы разложения.
Для каждой функции времени, входящей в уравнение Кирхгофа, описывающего расчетную цепь, устанавливается в соответствие операторное изображение, после чего система линейных дифференциальных уравнений переписывается в виде системы алгебраических уравнений (также получаем операторную схему замещения). Система алгебраических уравнений рассчитывается относительно операторного изображения искомой величины, по которому с помощью теоремы разложения находится оригинал.
Теорема разложения имеет две модификации в зависимости от вида операторного изображения искомой величины:
1)
=
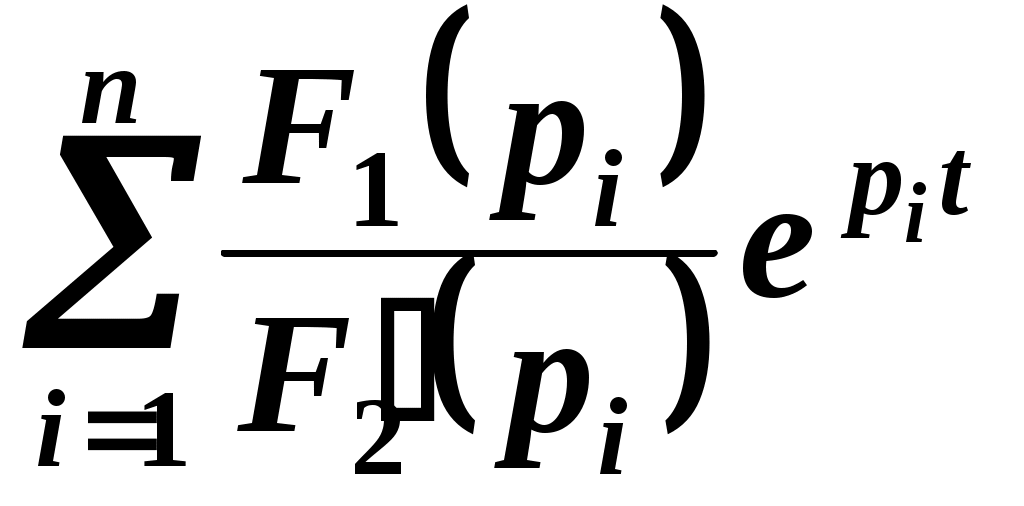, (2.2)где n – порядок цепи,
pi