Добавлен: 04.12.2023
Просмотров: 25
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– простые корни характеристического уравнения N(p) = 0;
.
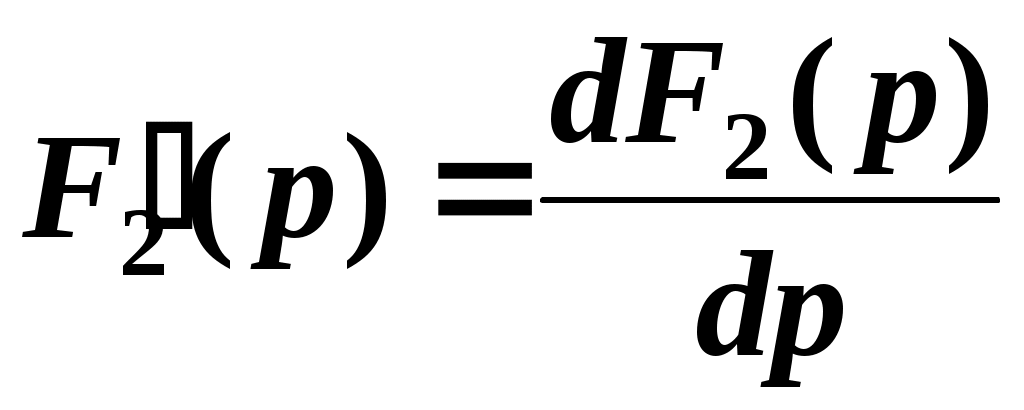2)
=
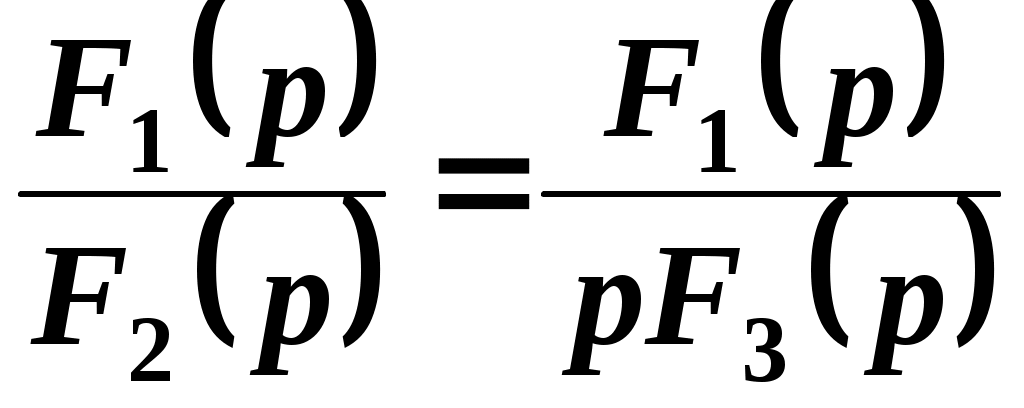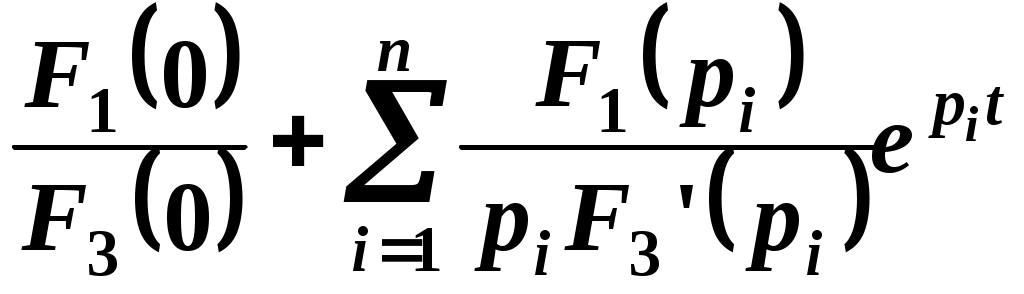, (2.3)
где pi – корни характеристического уравнения F3(p)=0.
В этом случае знаменатель имеет один нулевой корень, на это указывает наличие в составе знаменателя множителя p. Теорема разложения в форме (2.3) соответствует сигналам, имеющим принужденную составляющую.
Если уравнение второго порядка, соответствующее цепи второго порядка, F2(p)=0 имеет комплексные сопряженные корни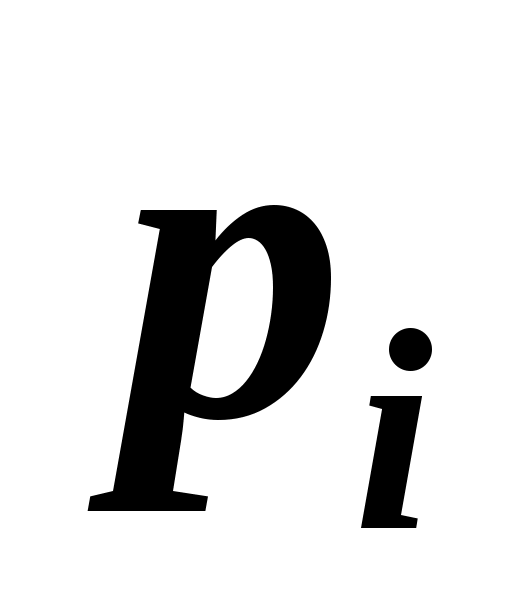
и 
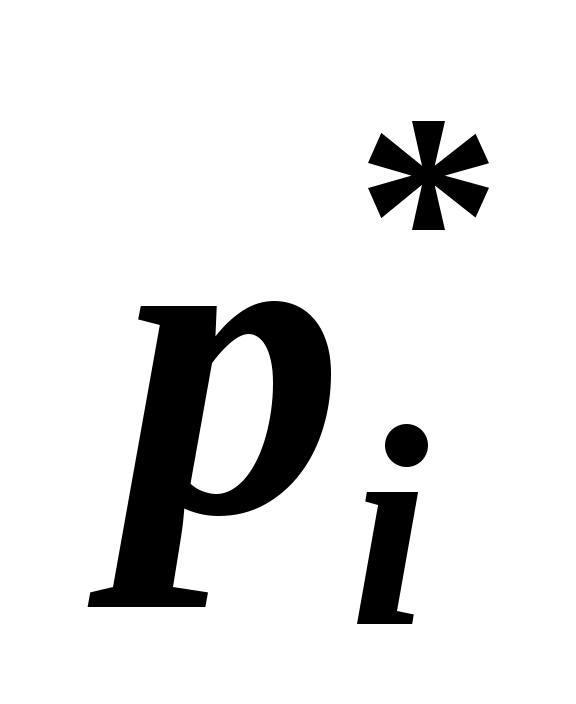, то достаточно вычислить слагаемое сумм (2.2) или (2.3) только для корня 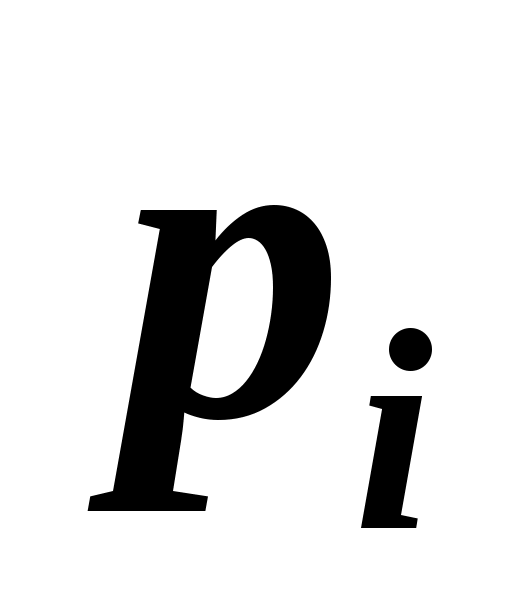, а для сопряженного корня 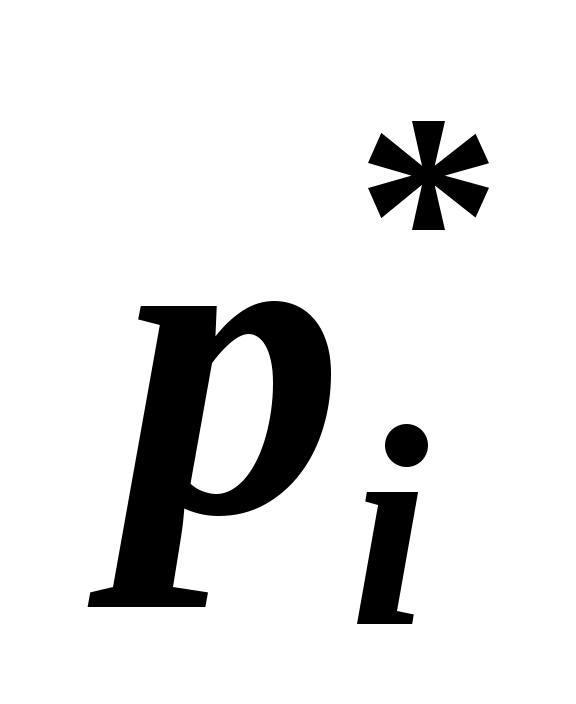взять значение, сопряженное этому слагаемому. Сумма, соответствующая этим двум слагаемым, равна удвоенному значению действительной части, найденной для одного из корней:
=
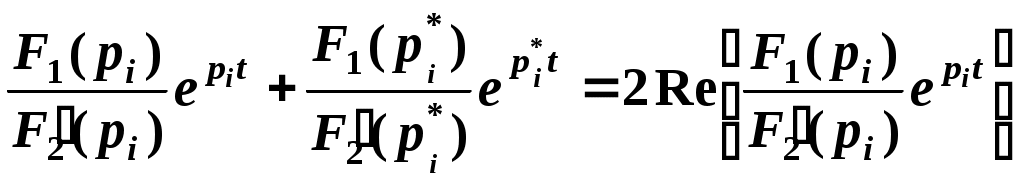(2.4)
или
=
.
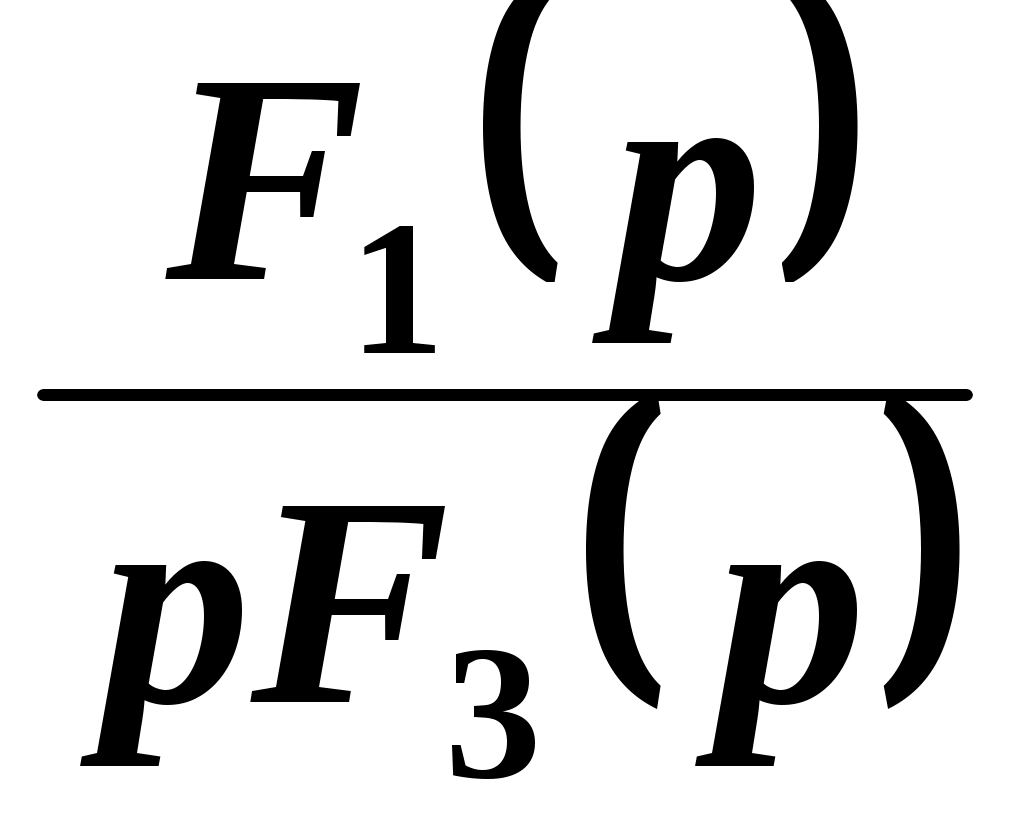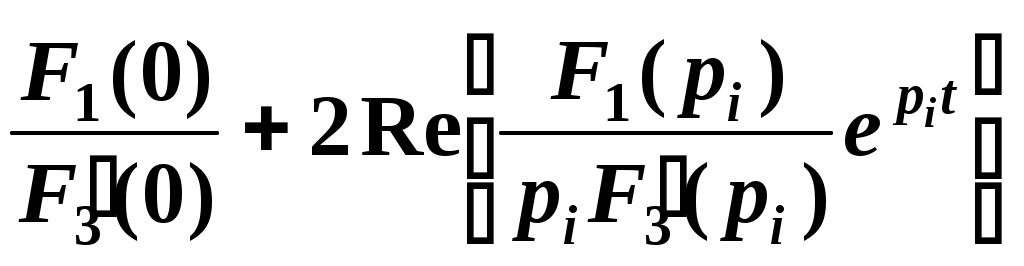3. Пример расчета переходного процесса
в цепи II порядка
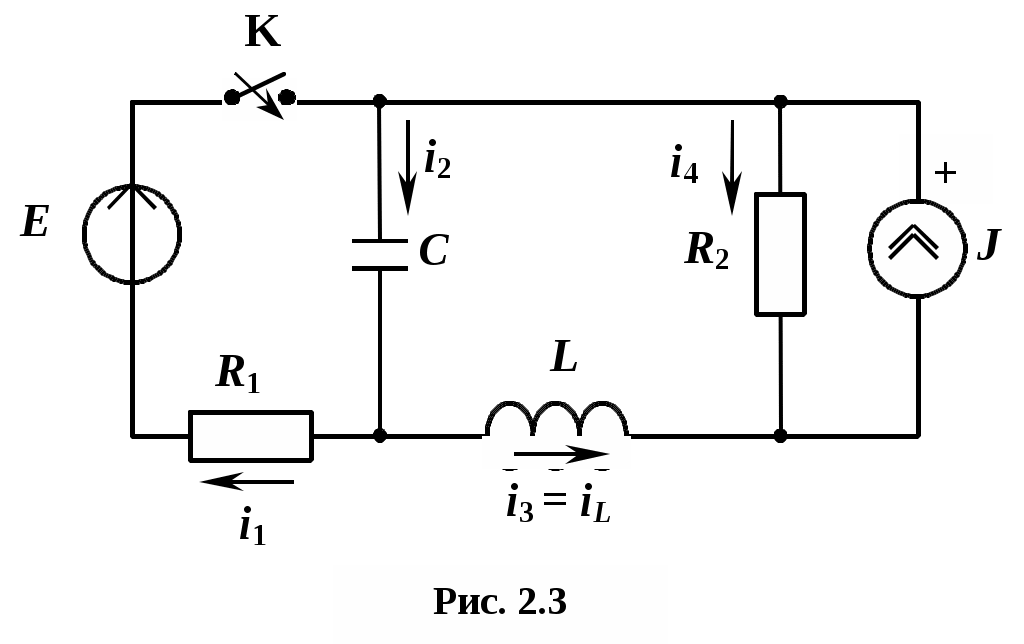
Дана цепь (рис. 2.3) с параметрами Е = 30 В , J = 2 А , R1 = 20 Ом , R2 = 10 Ом, С = 100 мкФ , L = 50 мГн .
Определить закон изменения тока i1(t) после коммутации.
iL(0–) = iL(0+) = 0 А,
uC(0–) = uC(0+) = J R2 = 20 B.
2.1. Совместное решение однородной системы дифференциальных уравнений. Составляем систему дифференциальных уравнений для мгновенных значений токов и напряжений по законам Кирхгофа:
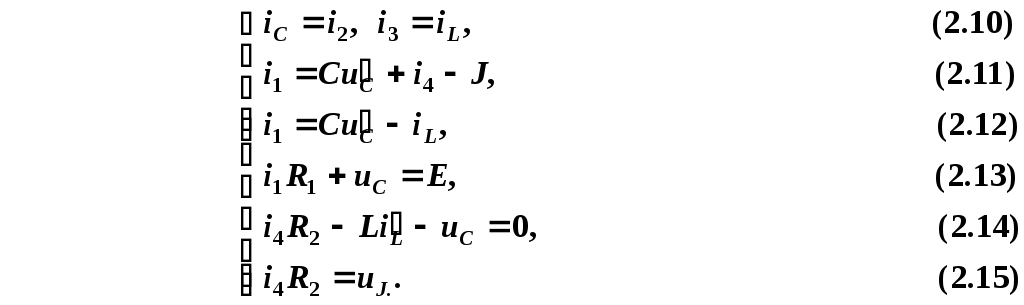Из уравнения (2.12)
.
Из уравнения (2.13) определим ток
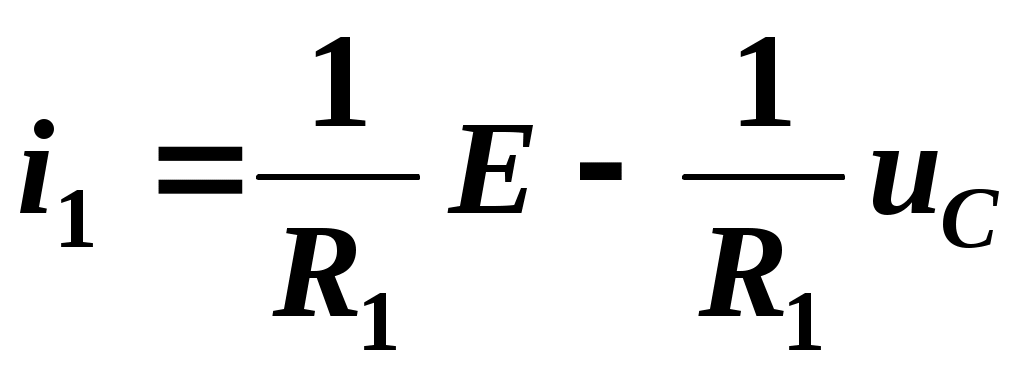(2.17)
и подставим его в выражение для тока индуктивности
.
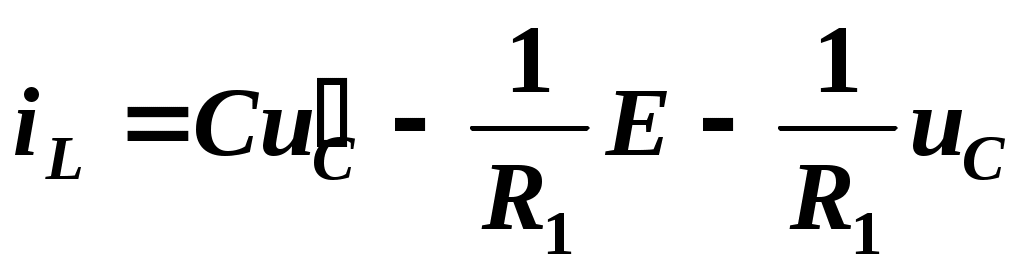Определим производную тока индуктивности
.
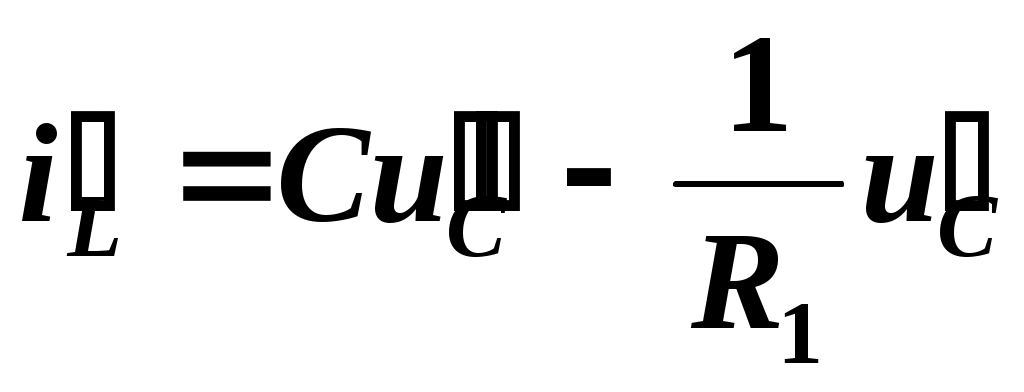Из уравнения (2.11) определим ток i4
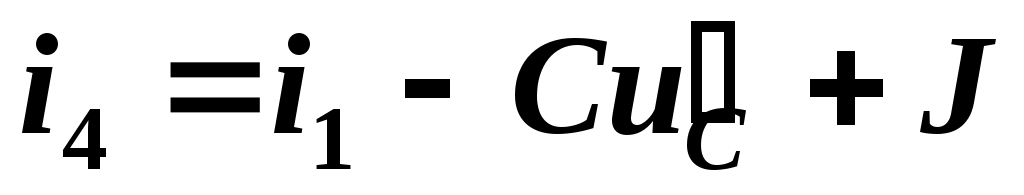
и подставим в полученное уравнение (2.17)
.
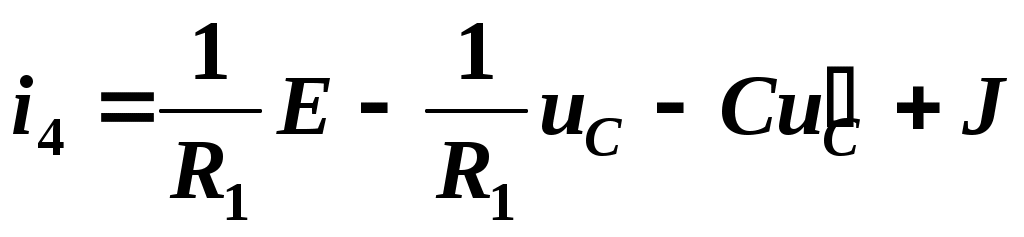Все полученные выражения подставляем в уравнение (2.14)
.
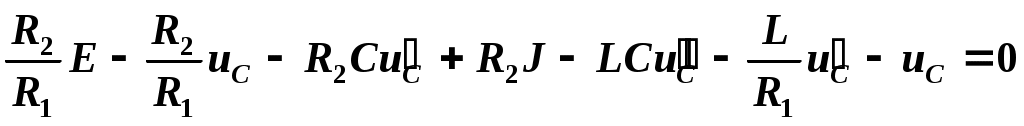После приведения подобных слагаемых и группирования получаем дифференциальное неоднородное уравнение второго порядка
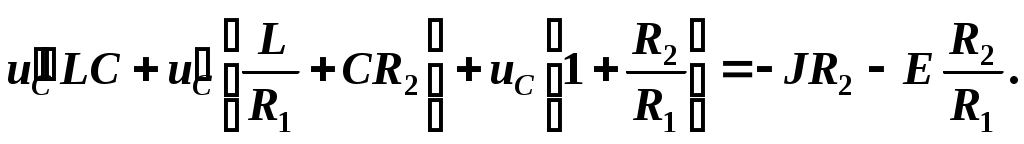
Таким образом методом исключения из системы дифференциальных уравнений для любой электрической цепи можно получить дифференциальное неоднородное уравнение.
Характеристическое уравнение получается из соответствующего однородного дифференциального уравнения в результате замены производных на соответствующие степени оператора p и имеет вид
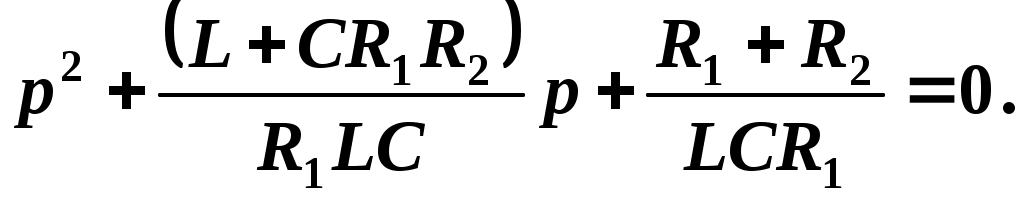
2.2. Алгебраизация дифференциальных уравнений. Для получения характеристических уравнений записывается система уравнений по методу контурных токов, которая впоследствии переписывается в алгебраической форме с помощью вспомогательного символа p, заменяющего операцию дифференцирования, и 1/p, заменяющего операцию интегрирования:
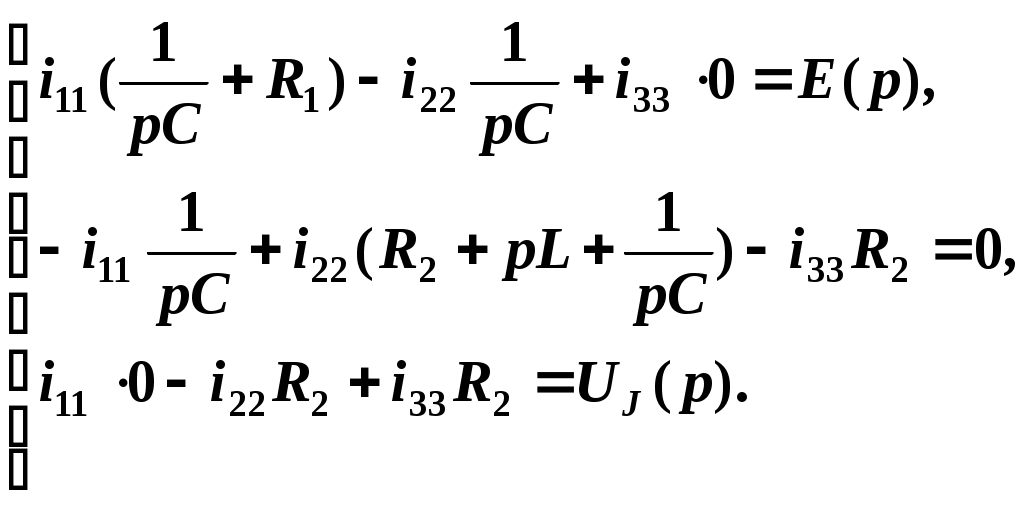
Так как i33 = J , следовательно,
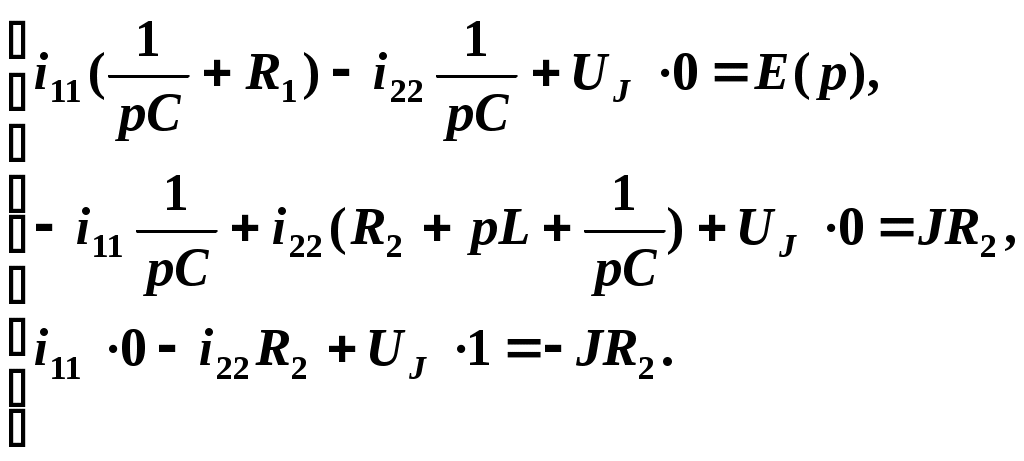
и, соответственно, для свободных составляющих токов:
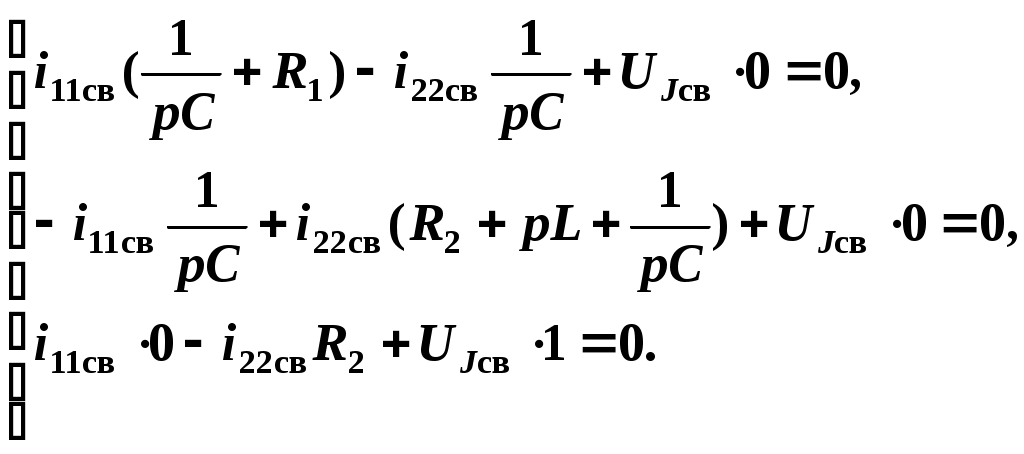
Данная система алгебраических уравнений имеет решение, отличное от нулевого только тогда, когда ее определитель равен нулю:
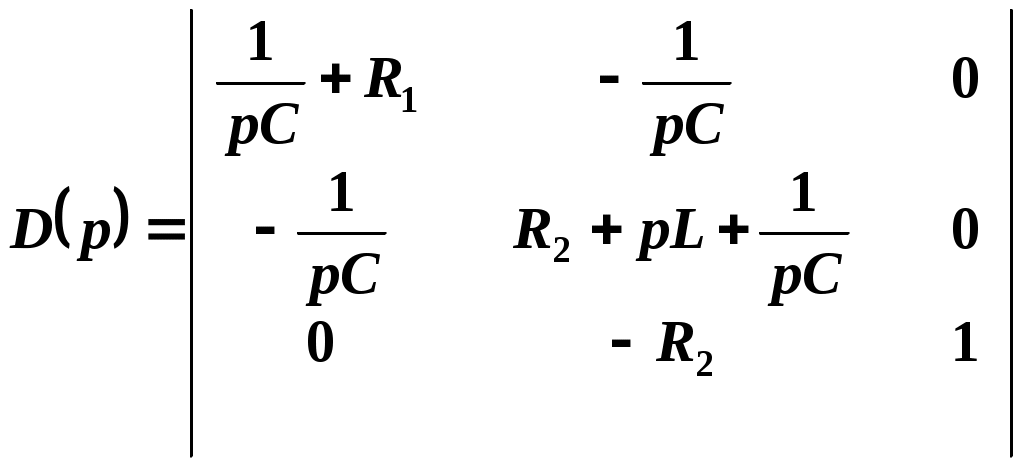
или
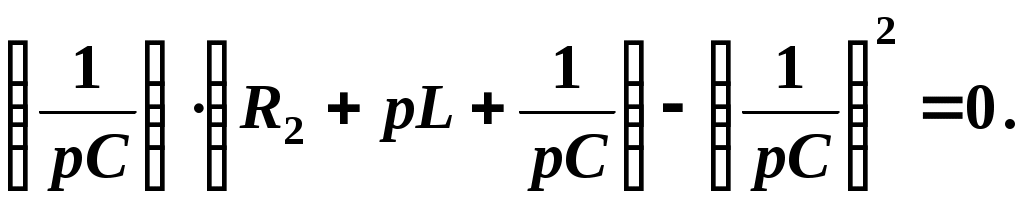
Таким образом, характеристическое уравнение в результате преобразования принимает вид
.
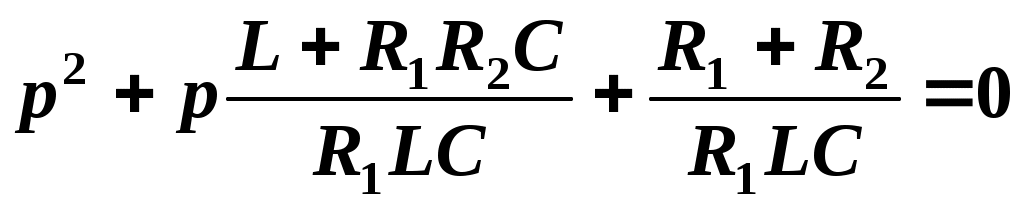2.3. Метод входного сопротивления. Удалим источники из цепи в соответствии с известным правилом: источники ЭДС заменяются короткозамкнутыми участками, ветви с источниками тока размыкаются.
В произвольной ветви, разорвав цепь, запишем входное сопротивление:
Заменив j на p, получим
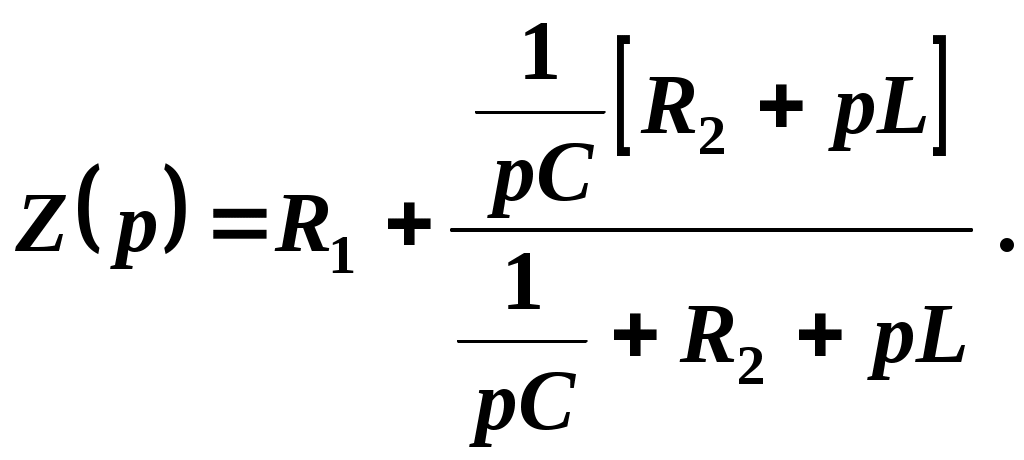
Приравняв данное выражение нулю (Z(р) = 0) и произведя необходимые преобразования, получим характеристическое уравнение цепи
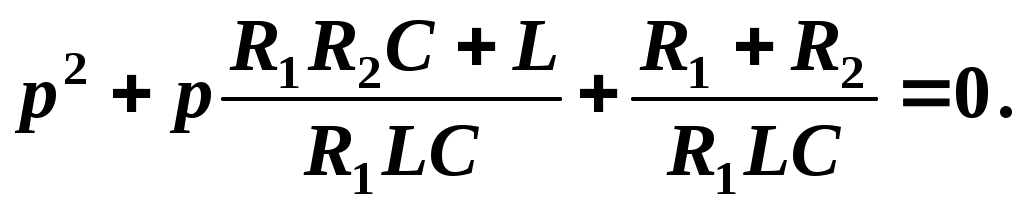
Подставим значения параметров цепи:
p2 + 700p + 300000 = 0.
Корни характеристического уравнения
p1 = – 350 + j421,308, p2
= – 350 – j421,308
являются комплексными сопряженными, следовательно, переходный процесс в цепи имеет колебательный характер.
,
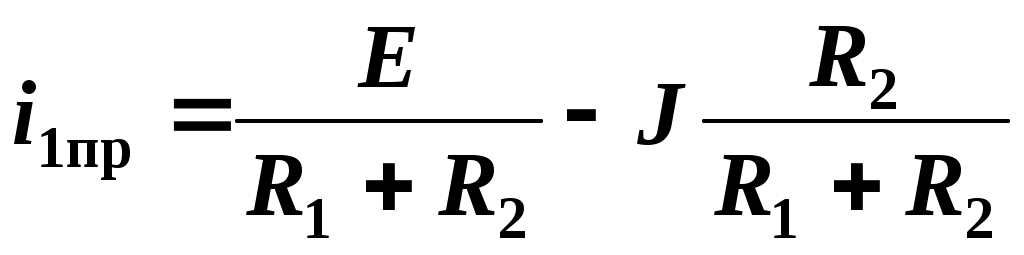i1пр = 1/3 (A).
4. Определение свободной составляющей. Для цепей, характеристические числа которых имеют комплексные сопряженные значения, свободная составляющая определяется в виде
i1св(t) = e–t(A1cos t + A2 sin t),
где – декремент затухания, – частота свободных колебаний определяются через корни характеристического уравнения p1,2 = – + j.
Таким образом, в выражении i1св необходимо определить постоянные интегрирования А1 и А2. Вычисление их ведется с помощью системы уравнений, составленных для момента t = 0+:
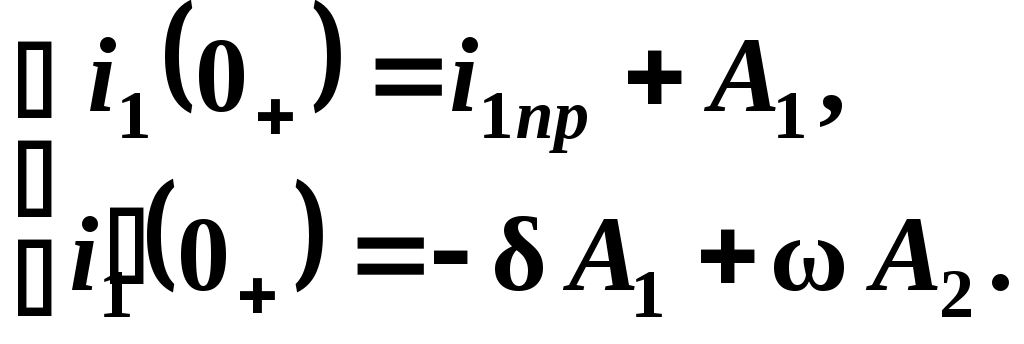
4.1. Определение значени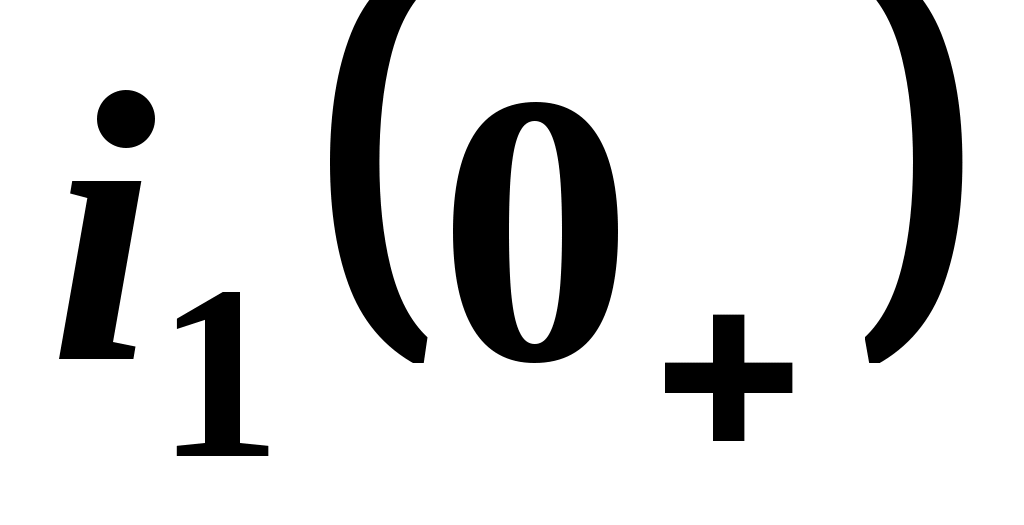й
и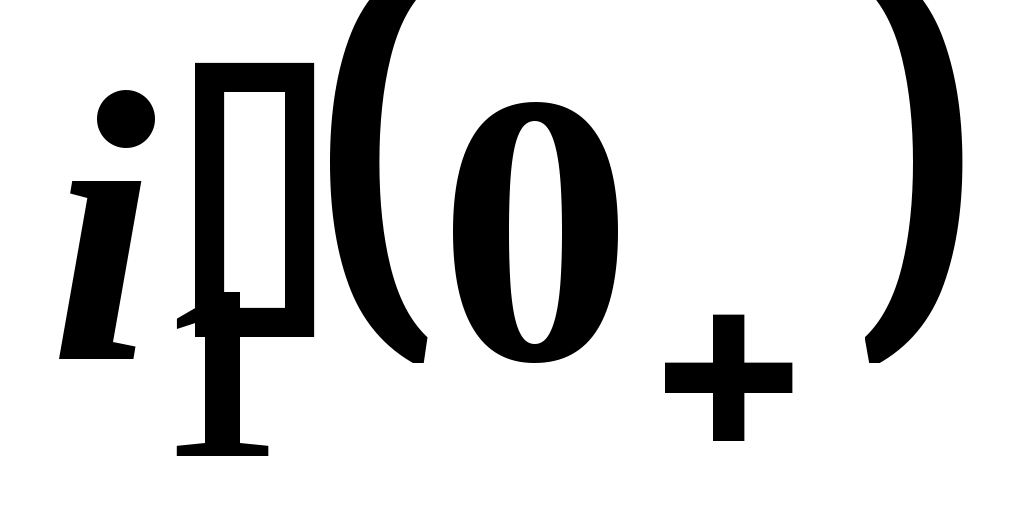 
с использованием системы уравнений Кирхгофа. В данном случае cоставляется система уравнений Кирхгофа. Методом исключения выражается значение тока i1(0+) через известные значения uC(0+) и i2(0+):
.
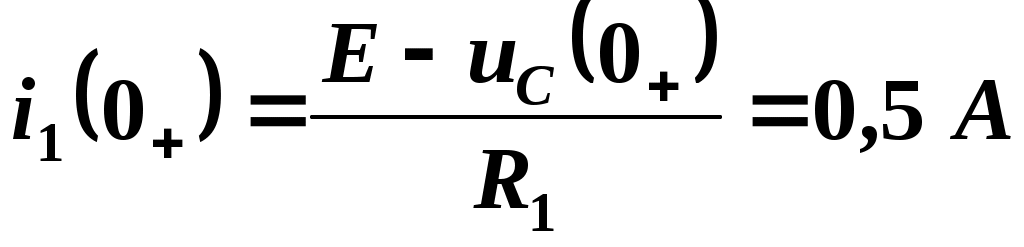Дифференцируя выражение для i1(t), получим
.
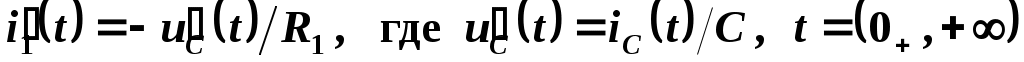Произведя необходимые преобразования и подстановки в системе уравнений Кирхгофа, получим
.
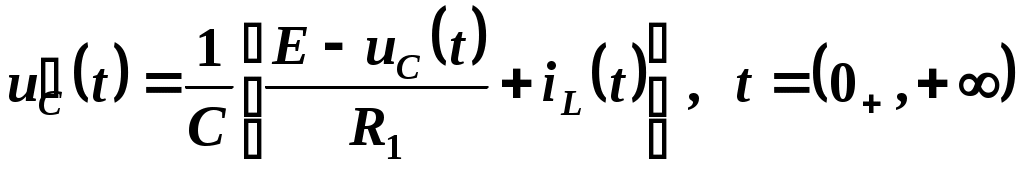Подставив соответствующие значения
uC и iL в момент t = 0+, рассчитаем
i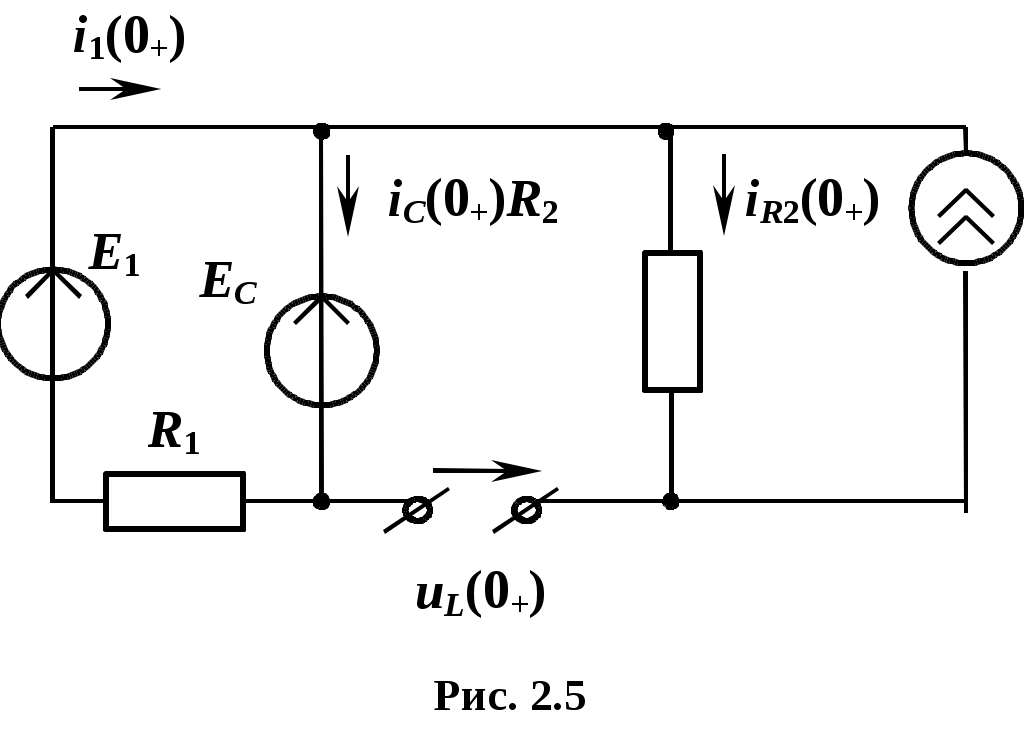
1(0+) = – 250 A/с.
4.2. Определение i1(0+) и i1(0+) с использованием резистивных схем замещения в момент t = 0+. Схема замещения в 0+ для величин токов и напряжений изображена на рис. 2.5
ЕС = uС(0–)
J = iL(0–)
J
По II закону Кирхгофа получим
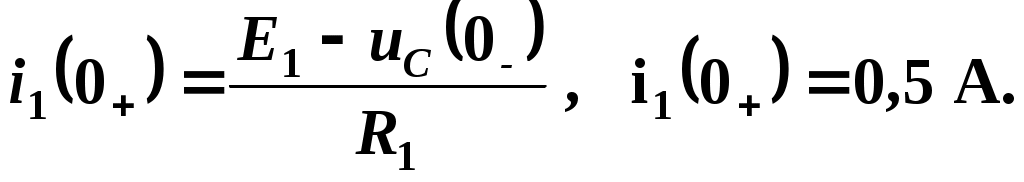
Для построения схемы замещения в (0+) для производных токов и напряжений необходимо определить начальные значения:
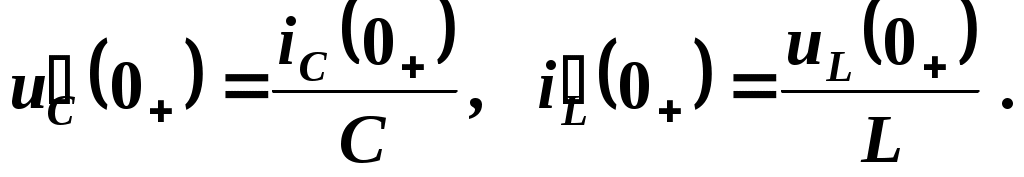
Таким образом, следует определить iC(0+) и uL(0+) с помощью уже полученной схемы замещения:
а) для определения uL(0+) составим уравнение по II закону Кирхгофа:
uL(0+) – iR2(0+)R2 = – uC(0+)
подставив значения, получим uL(0+) = 0, следовательно,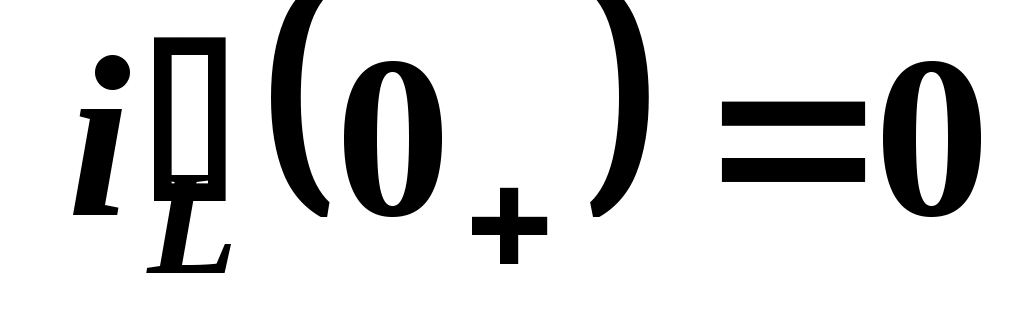
.
б) iC(0+) = i1(0+) = 0,5 A , следовательно,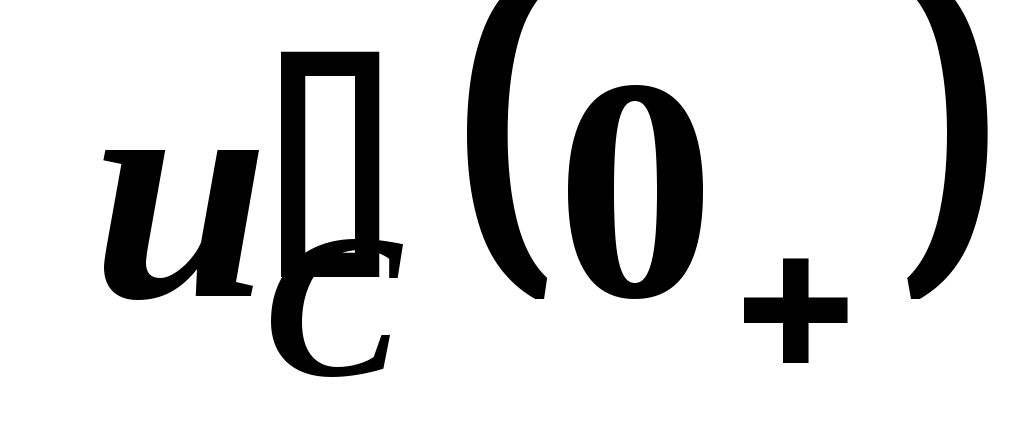
= 5000 B/с.
При построении схемы замещения в 0+ для производных следует:
.2)
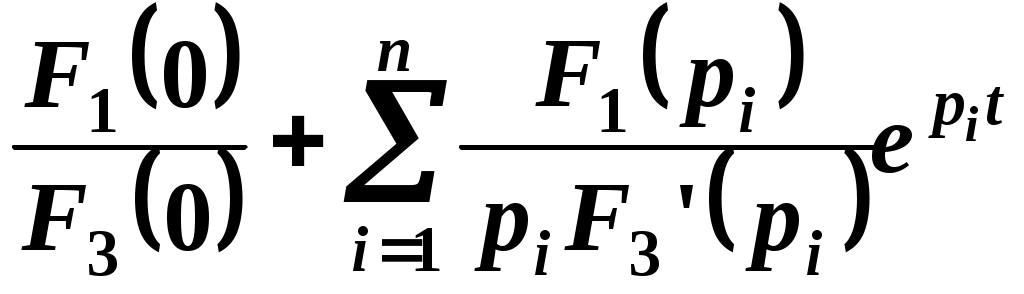= , (2.3)где pi – корни характеристического уравнения F3(p)=0.
В этом случае знаменатель имеет один нулевой корень, на это указывает наличие в составе знаменателя множителя p. Теорема разложения в форме (2.3) соответствует сигналам, имеющим принужденную составляющую.
Если уравнение второго порядка, соответствующее цепи второго порядка, F2(p)=0 имеет комплексные сопряженные корни
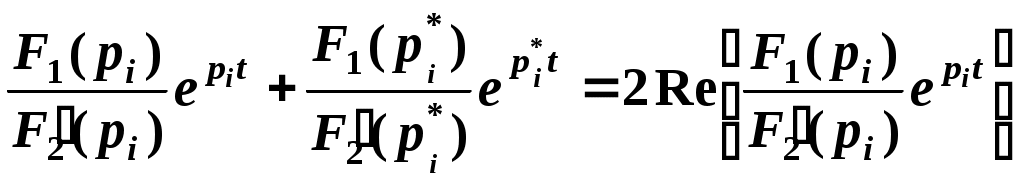и , то достаточно вычислить слагаемое сумм (2.2) или (2.3) только для корня , а для сопряженного корня взять значение, сопряженное этому слагаемому. Сумма, соответствующая этим двум слагаемым, равна удвоенному значению действительной части, найденной для одного из корней: = (2.4)или
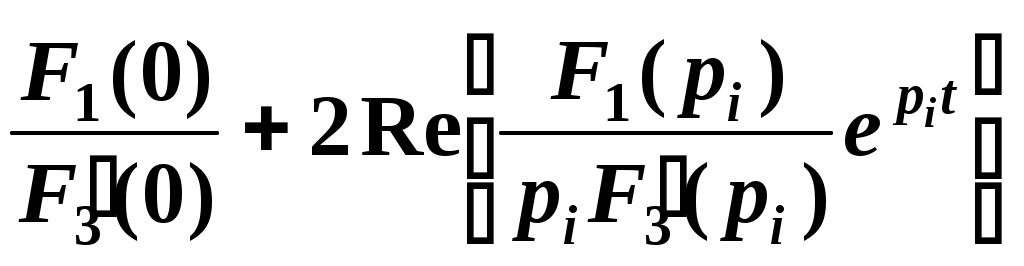= .3. Пример расчета переходного процесса
в цепи II порядка
Дана цепь (рис. 2.3) с параметрами Е = 30 В , J = 2 А , R1 = 20 Ом , R2 = 10 Ом, С = 100 мкФ , L = 50 мГн .
Определить закон изменения тока i1(t) после коммутации.
3.1. Классический метод расчета
-
Правила коммутации:
iL(0–) = iL(0+) = 0 А,
uC(0–) = uC(0+) = J R2 = 20 B.
-
Составление характеристического уравнения цепи.
2.1. Совместное решение однородной системы дифференциальных уравнений. Составляем систему дифференциальных уравнений для мгновенных значений токов и напряжений по законам Кирхгофа:
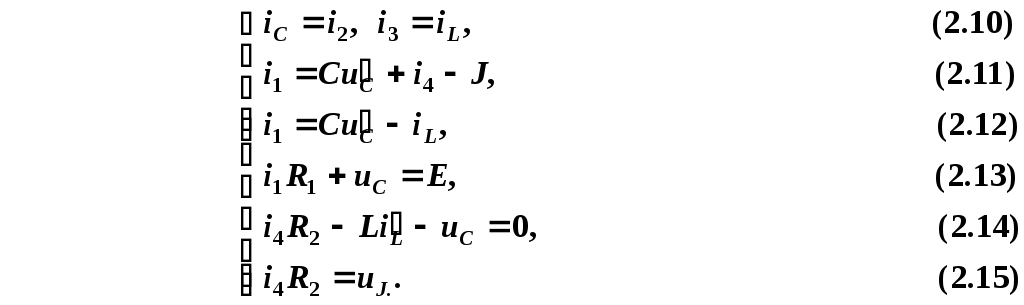Из уравнения (2.12) .Из уравнения (2.13) определим ток
(2.17)и подставим его в выражение для тока индуктивности
.Определим производную тока индуктивности
.Из уравнения (2.11) определим ток i4
и подставим в полученное уравнение (2.17)
.Все полученные выражения подставляем в уравнение (2.14)
.После приведения подобных слагаемых и группирования получаем дифференциальное неоднородное уравнение второго порядка
Таким образом методом исключения из системы дифференциальных уравнений для любой электрической цепи можно получить дифференциальное неоднородное уравнение.
Характеристическое уравнение получается из соответствующего однородного дифференциального уравнения в результате замены производных на соответствующие степени оператора p и имеет вид
2.2. Алгебраизация дифференциальных уравнений. Для получения характеристических уравнений записывается система уравнений по методу контурных токов, которая впоследствии переписывается в алгебраической форме с помощью вспомогательного символа p, заменяющего операцию дифференцирования, и 1/p, заменяющего операцию интегрирования:
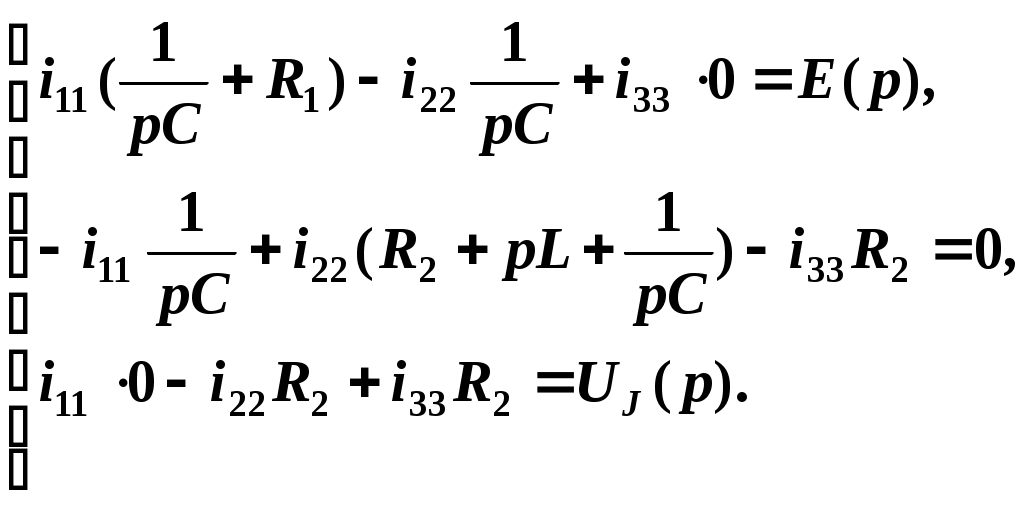
Так как i33 = J , следовательно,
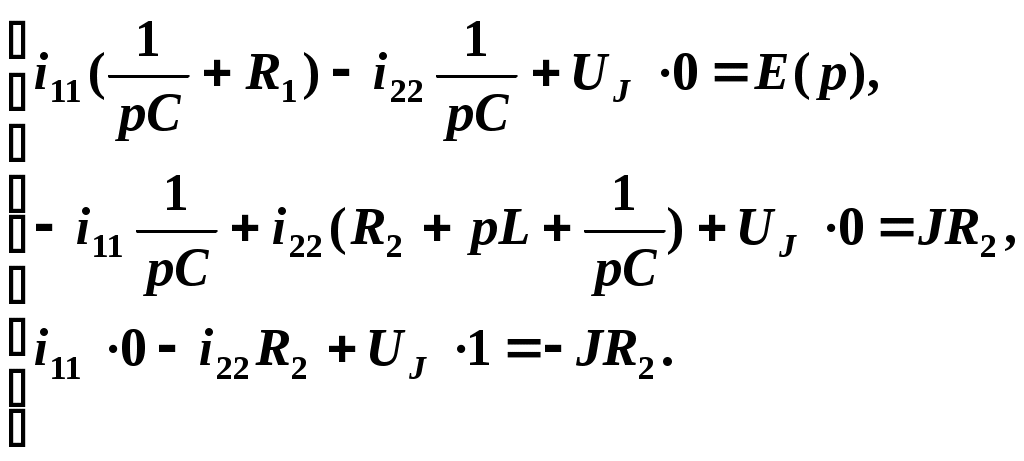
и, соответственно, для свободных составляющих токов:
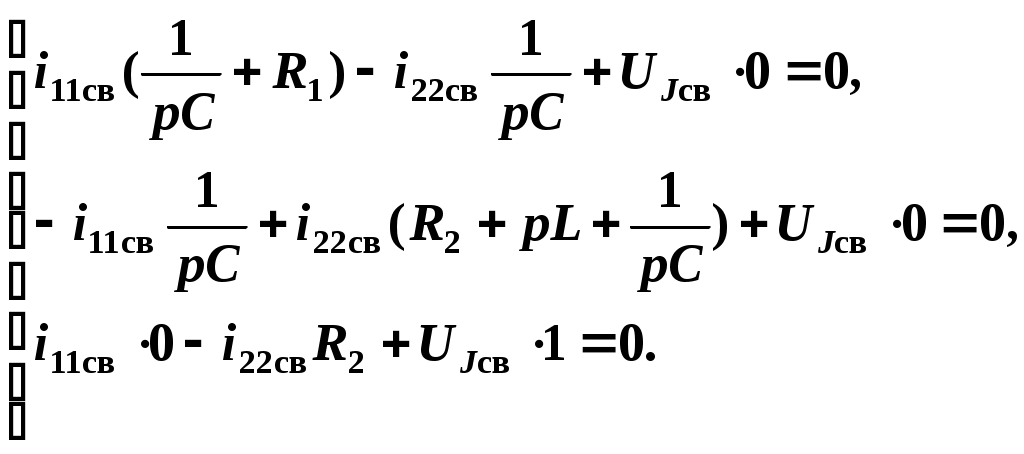
Данная система алгебраических уравнений имеет решение, отличное от нулевого только тогда, когда ее определитель равен нулю:
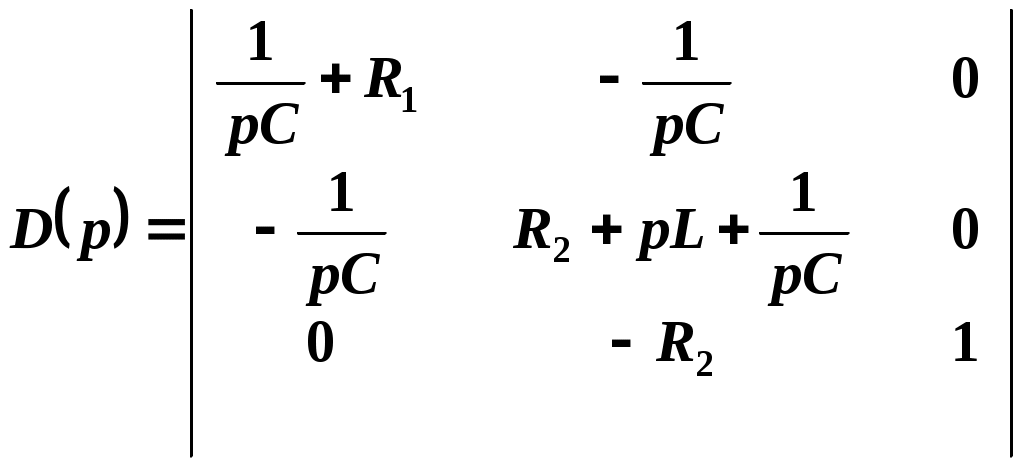
или
Таким образом, характеристическое уравнение в результате преобразования принимает вид
.2.3. Метод входного сопротивления. Удалим источники из цепи в соответствии с известным правилом: источники ЭДС заменяются короткозамкнутыми участками, ветви с источниками тока размыкаются.
В произвольной ветви, разорвав цепь, запишем входное сопротивление:
Заменив j на p, получим
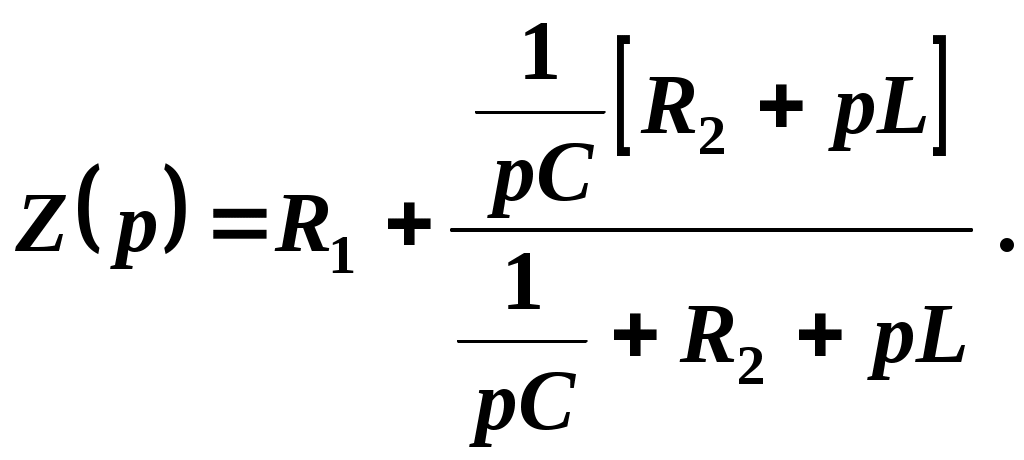
Приравняв данное выражение нулю (Z(р) = 0) и произведя необходимые преобразования, получим характеристическое уравнение цепи
Подставим значения параметров цепи:
p2 + 700p + 300000 = 0.
Корни характеристического уравнения
p1 = – 350 + j421,308, p2
= – 350 – j421,308
являются комплексными сопряженными, следовательно, переходный процесс в цепи имеет колебательный характер.
-
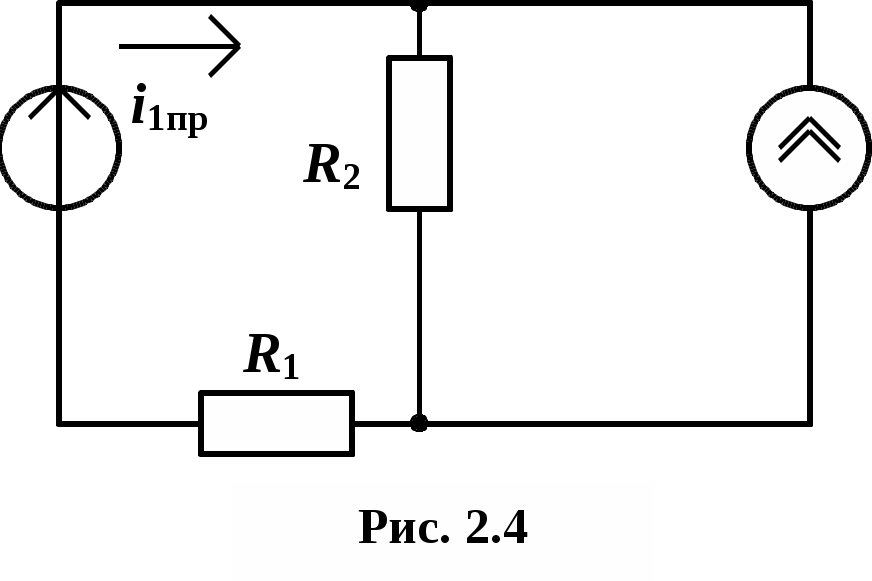
Определение принужденной составляющей. Рассматриваемая цепь в принужденном режиме имеет вид (рис. 2.4)
,i1пр = 1/3 (A).
4. Определение свободной составляющей. Для цепей, характеристические числа которых имеют комплексные сопряженные значения, свободная составляющая определяется в виде
i1св(t) = e–t(A1cos t + A2 sin t),
где – декремент затухания, – частота свободных колебаний определяются через корни характеристического уравнения p1,2 = – + j.
Таким образом, в выражении i1св необходимо определить постоянные интегрирования А1 и А2. Вычисление их ведется с помощью системы уравнений, составленных для момента t = 0+:
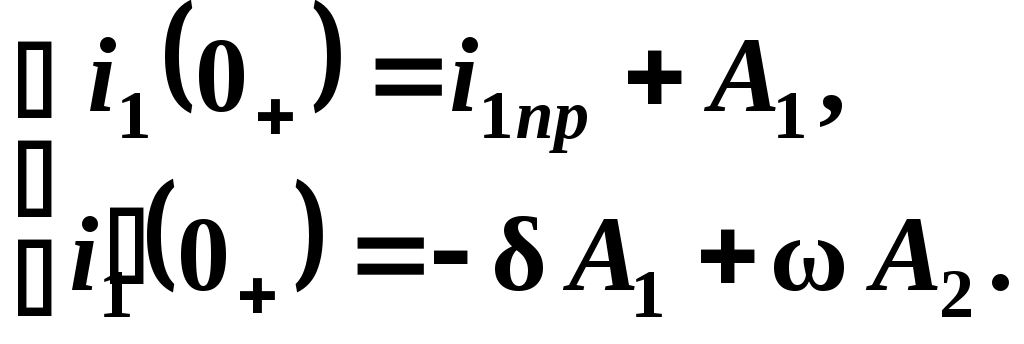
4.1. Определение значений
и с использованием системы уравнений Кирхгофа. В данном случае cоставляется система уравнений Кирхгофа. Методом исключения выражается значение тока i1(0+) через известные значения uC(0+) и i2(0+): .Дифференцируя выражение для i1(t), получим
.Произведя необходимые преобразования и подстановки в системе уравнений Кирхгофа, получим
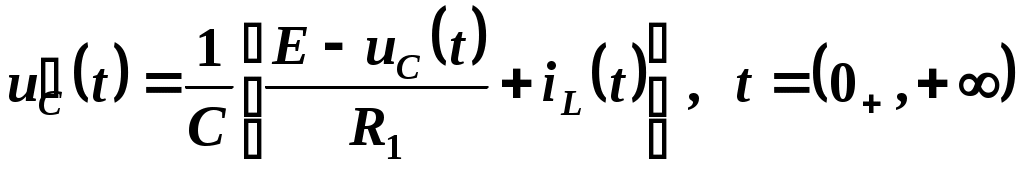.Подставив соответствующие значения
uC и iL в момент t = 0+, рассчитаем
i
1(0+) = – 250 A/с.4.2. Определение i1(0+) и i1(0+) с использованием резистивных схем замещения в момент t = 0+. Схема замещения в 0+ для величин токов и напряжений изображена на рис. 2.5
ЕС = uС(0–)
J = iL(0–)
J
По II закону Кирхгофа получим
Для построения схемы замещения в (0+) для производных токов и напряжений необходимо определить начальные значения:
Таким образом, следует определить iC(0+) и uL(0+) с помощью уже полученной схемы замещения:
а) для определения uL(0+) составим уравнение по II закону Кирхгофа:
uL(0+) – iR2(0+)R2 = – uC(0+)
подставив значения, получим uL(0+) = 0, следовательно,
.б) iC(0+) = i1(0+) = 0,5 A , следовательно,
= 5000 B/с.При построении схемы замещения в 0+ для производных следует:
-
источники заменить на аналогичные источники с ЭДС или задающим током, равным соответственно производной от данных в задании; -
номиналы резисторов остаются неизменными; -
емкости и индуктивности же замещаются в соответствии со следующим правилом – емкости с нулевыми начальными условиями (
) заменяются короткозамкнутыми участками, с ненулевыми начальными условиями(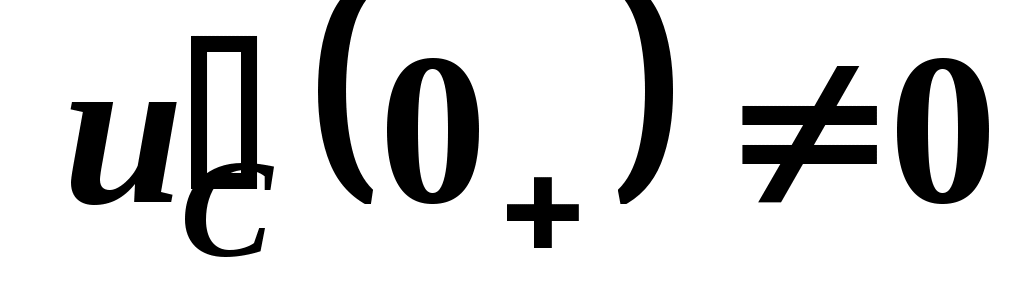
) – противодействующими источниками ЭДС с 
; -
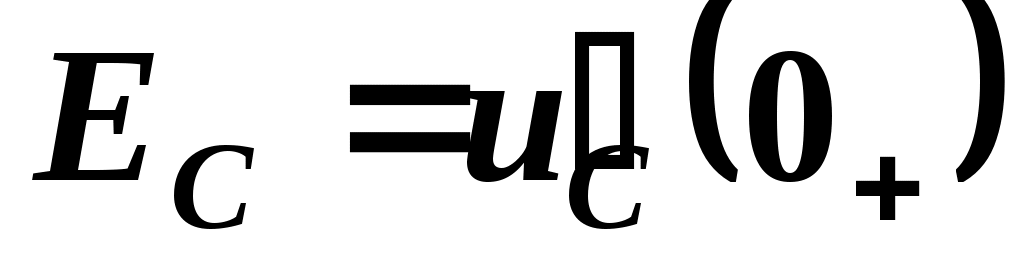ветви с индуктивностями, имеющими нулевые начальные условия (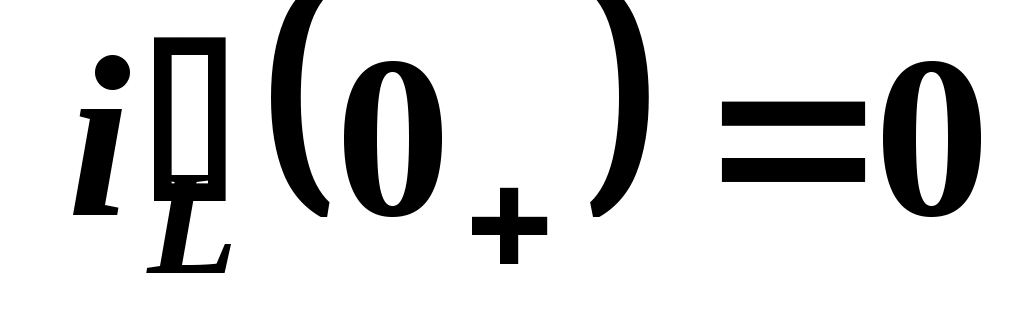 ) размыкаются, в случае ненулевых начальных условий (
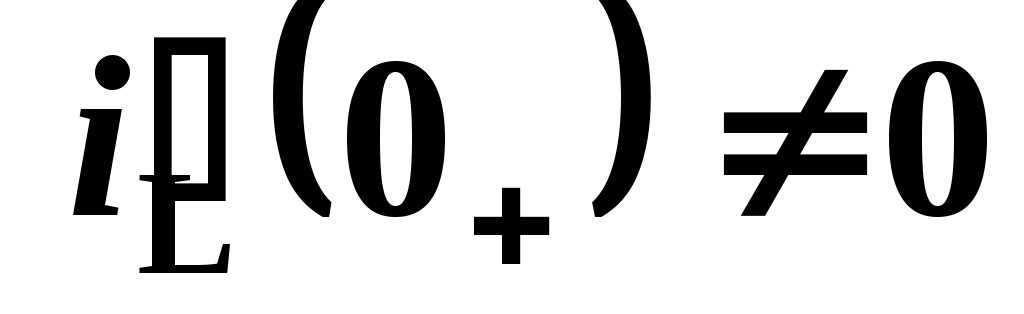) индуктивности заменяют на содействующие источники тока с 
.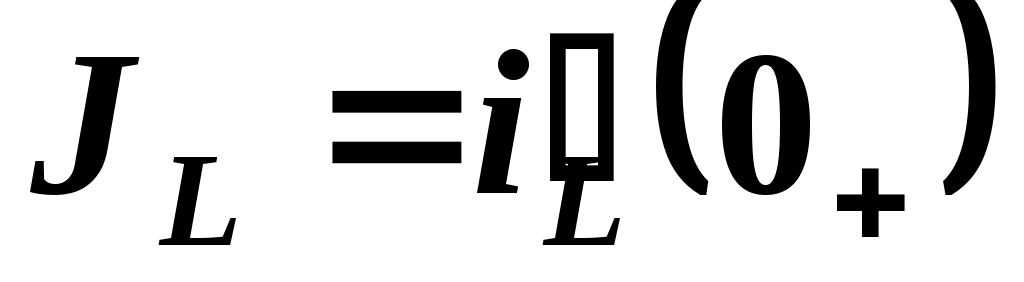