Таким образом, осуществляется операция дифференцирования, адекватная дифференцированию системы уравнений Кирхгофа.

В нашем случае, когда в цепи действуют источники постоянных воздействий, источники ЭДС заменяются короткозамкнутыми участками (т.к. ), а ветви с источниками тока размыкаются (т.к. ).

Т
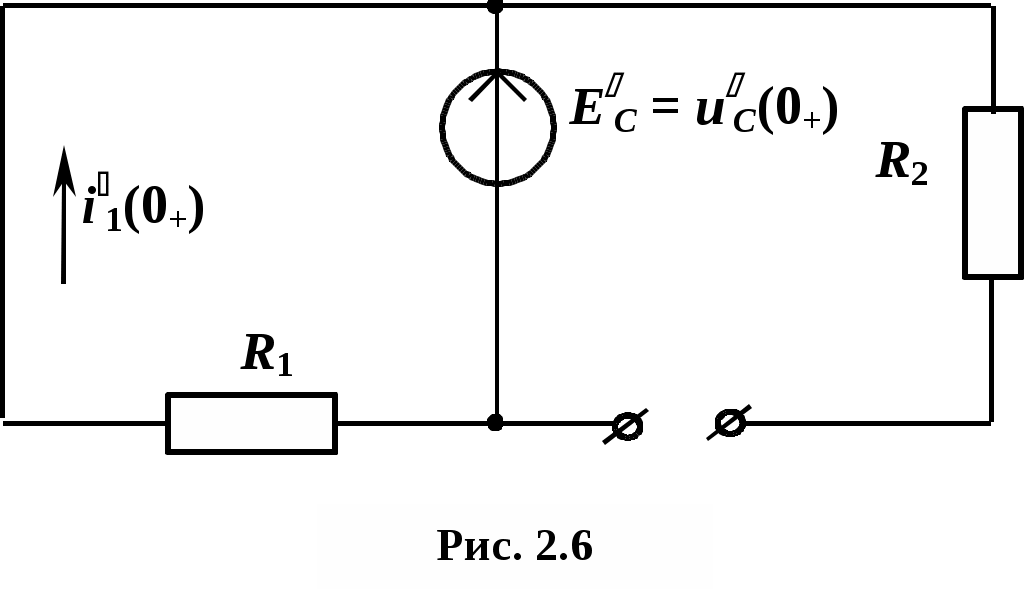
аким образом, схема замещения в t = 0₊ для производных имеет вид (рис. 2.6). Определим .

4.3. Определение постоянных интегрирования:



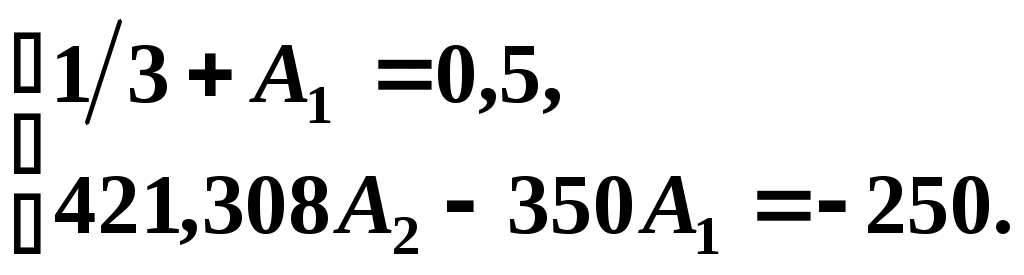
Решив данную систему уравнений, получим

А₁ = 0,1667, А₂ = – 0.455.

5. Определение полного решения. Полное решение следует искать в виде

i₁(t) = i_1пр + i_1св.

С учетом произведенных расчетов получим



Для удобства построения графика преобразуем полученное выражение в синусоидальную форму:



( + ) прибавляется к аргументу, так как угол  имеет отрицательный знак

и положительный знак ,

т.е. если рассматривать единичную окружность, данный угол находится во II четверти координатной плоскости.

Угол  определяется в радианах, так как свободная частота измеряется в рад/с. Таким образом, искомый ток

i₁(t) = 1/3 + e^–350t0,485 sin(421,308t + 2,788).

6. Построение графика изменения тока i(t). Оценим соотношение между постоянной времени экспоненты и периодом синусоиды. Постоянная времени экспоненты _exp

---

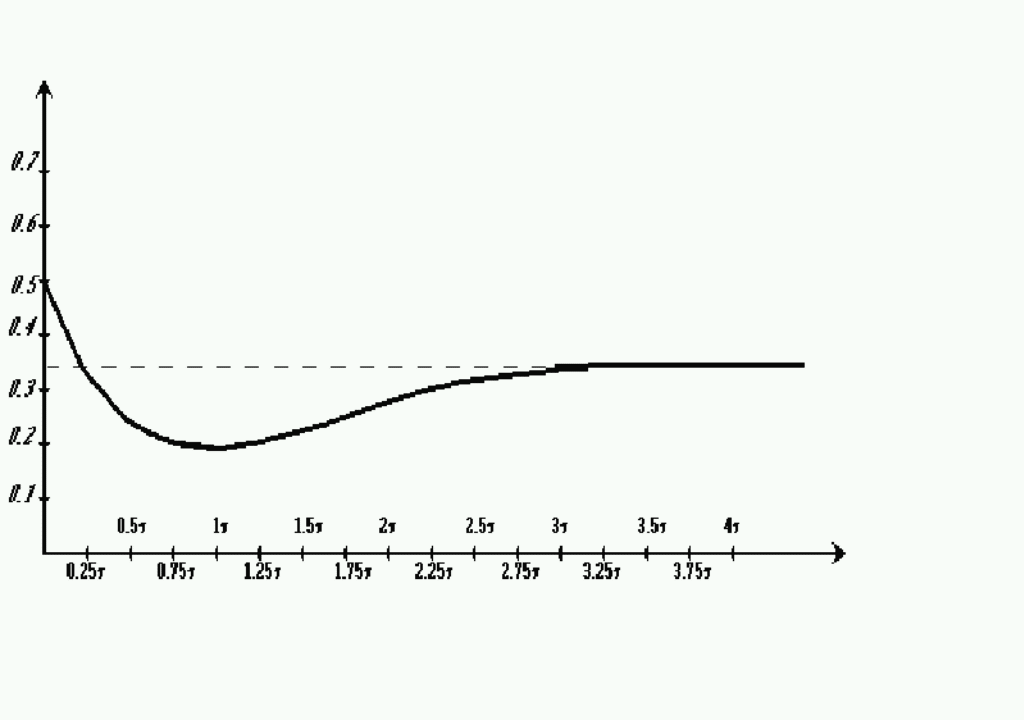
= 1/ = 0,00286 с. Период синусоиды T_sin = 1/f = 2/ = 0,0149 с. В связи с тем, что _ехр << T_sin, график строится по точкам. Результаты расчетов значений тока i₁(t) записаны в табл. 2.2., а график изменения i₁(t) изображен на рис. 2.7.

Таблица 2.2

t	i1(t)	t	i1(t)	t	i1(t)
0	0,5	2 	0,2754	4 	0,3419
0,25 	0,3531	2,25 	0,2973	4,25 	0,3402
0,5 	0,2609	2,5 	0,3149	4,5 	0,3384
0,75 	0,2137	2,75 	0,3278	4,75 	0,3366
1 	0,1993	3 	0,3362	5 	0,3352
1,25 	0,2065	3,25 	0,3410	5,25 	0,3341
1,5 	0,2260	3,5 	0,3430	5,5 	0,3333
1,75 	0,2506	3,75 	0,3430

Рис 2.7.
б
3.2. Операторный метод

С учетом независимых начальных условий изображается операторная схема замещения (рис. 2.8).

У
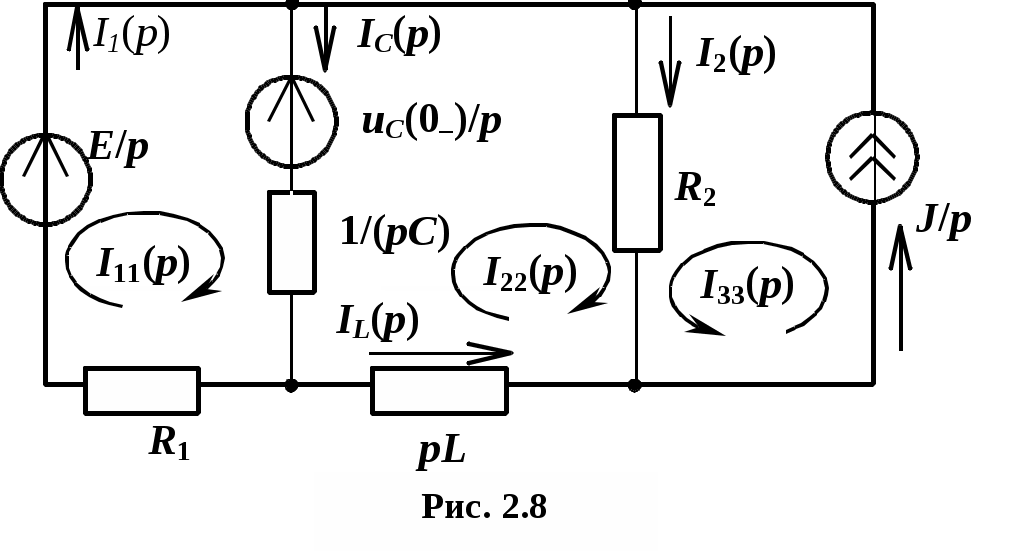
равнения Кирхгофа в операторной форме запишутся в виде

---

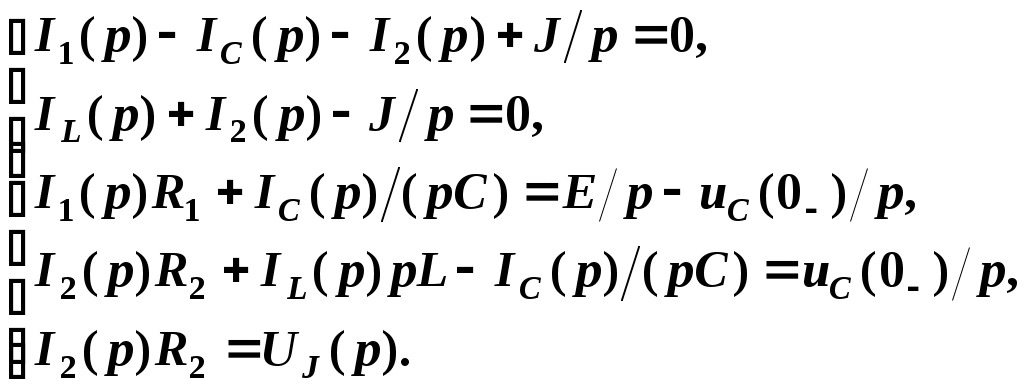
Решение получается проще при использовании метода контурных токов. Контурные токи выберем так, как показано на рис. 2.8.

Ток , тогда система уравнений имеет вид:



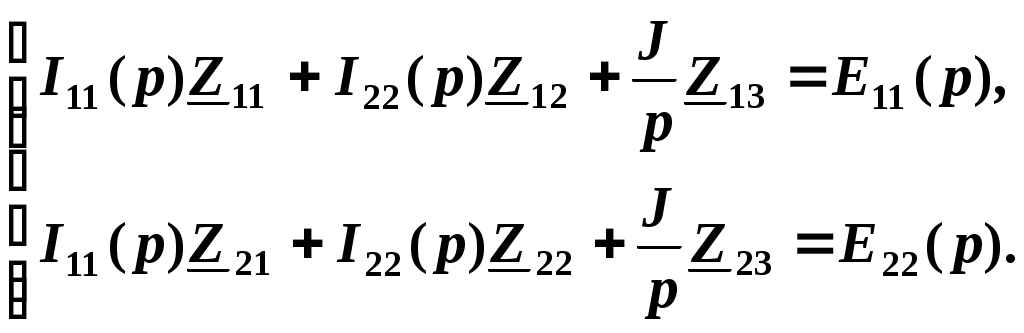
Определим собственные и общие сопротивления, а также контурные ЭДС, полученные выражения подставим в систему уравнений:



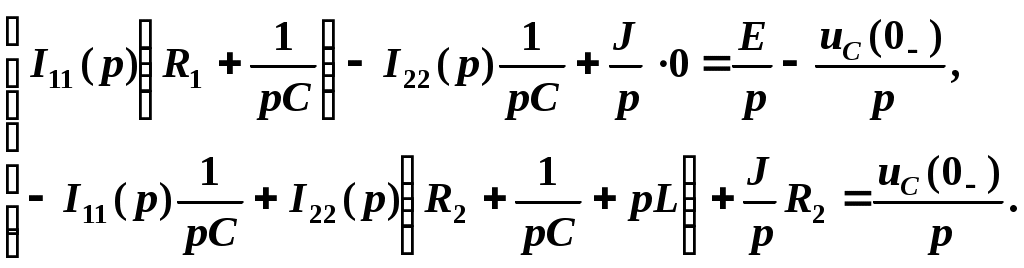
После преобразований



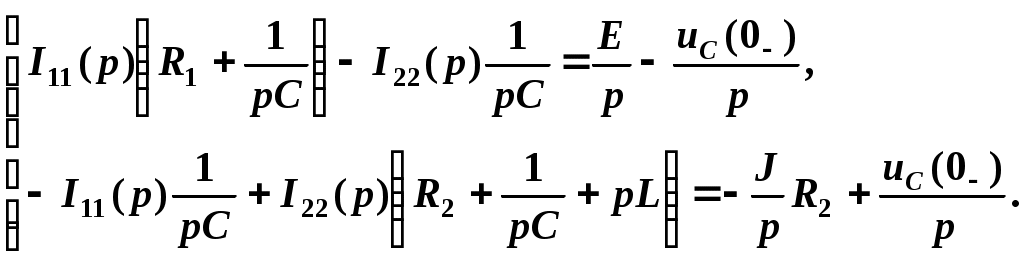
Подставим значения



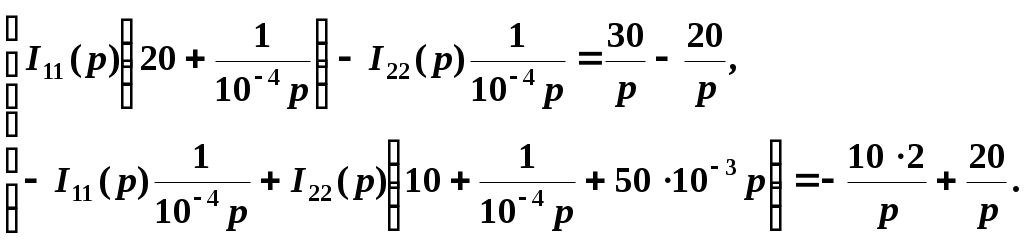
Решим систему уравнений при помощи метода определителей:

,

.

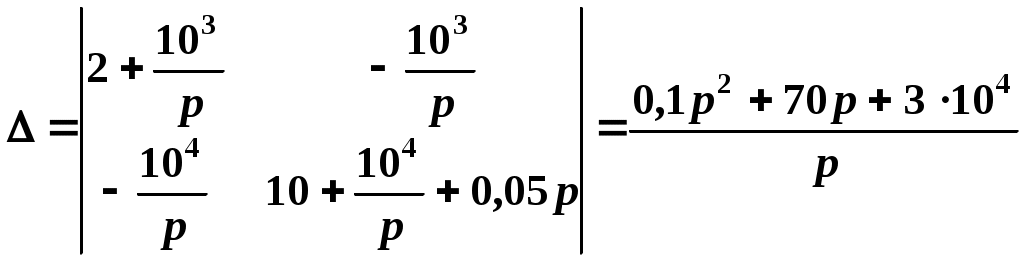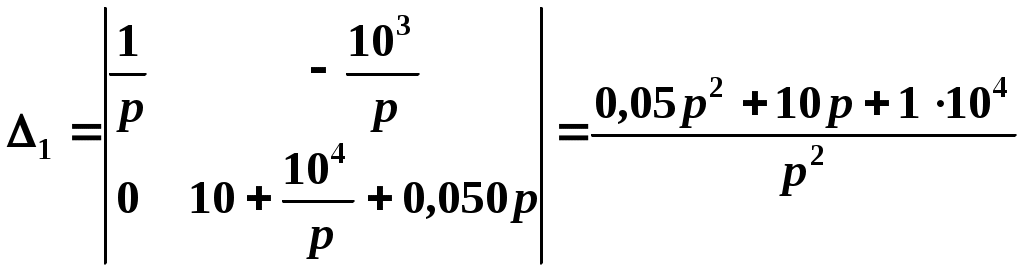Изображение тока в первой ветви определится

.

Определим оригинал искомого тока с помощью теоремы разложения. Многочлен второй степени знаменателя приравняем нулю и получим характеристическое уравнение цепи , решением которого являются комплексные сопряженные корни

,

которые совпадают с полученными при решении классическим методом.

Оригинал тока определяем по формуле (2.4). Вычислим производную и значение производной, а также значение многочлена при корне , подставим в (2.4):

,

---

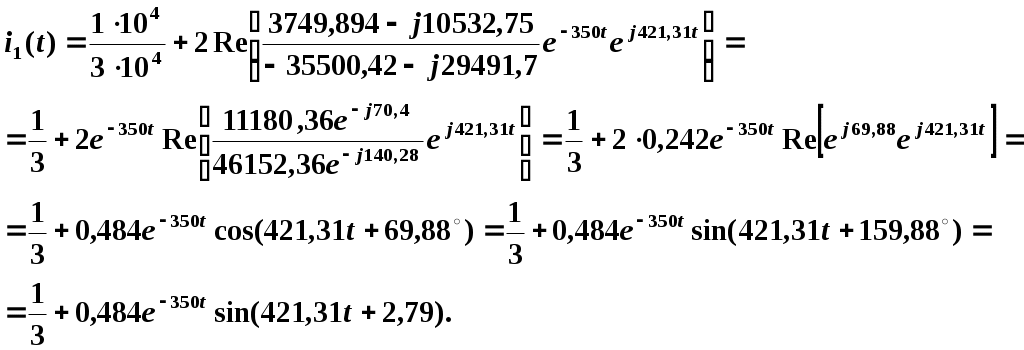Данное решение совпадает с решением, полученным классическим методом.

---

Смотрите также файлы

• Шалун .docx

• 1 высокая содержательная сложность.docx

• Как рисовать законы содержания и оформления.pdf

• Горного производства Лабораторная работа исследование гранулометрического состава разрушенных скальных пород.docx

• Intertidal приливный.docx