Частное профессиональное образовательное учреждение «ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»

Практическое задание

по	Статистике

дисциплине

Выполнил(а) студент(ка)	Карпова Валерия Расимяновна
			фамилия имя отчество
Идентификационный номер:		2201-0210-2201389

Пермь 2022Задача 1. Имеются следующие данные за год по заводам одной промышленной компании:

Завод	Среднее число рабочих, чел.	Основные фонды, млн руб.	Продукция, млн руб.	Завод	Среднее число рабочих, чел.	Основные фонды, млн руб.	Продукция, млн руб.
1	700	250	300	9	1 400	1 000	1 600
2	800	300	360	10	1 490	1 250	1 800
3	750	280	320	11	1 600	1 600	2 250
4	900	400	600	12	1 550	1 500	2 100
5	980	500	800	13	1 800	1 900	2 700
6	1 200	750	1 250	14	1 700	1 750	2 500
7	1 100	700	1 000	15	1 900	2 100	3 000
8	1 300	900	1 500

---

На основании приведенных данных составьте групповую таблицу зависимости выработки на одного рабочего от величины заводов по числу рабочих. Число групп – три.Решение:Произведем группировку заводов по числу рабочих. Величину интервала в группе определим по формуле:h = (X_max - X_min) / n = (1900 – 700) / 3 = 400 чел.Группировка заводов по числу рабочих.

	Группы заводов по числу рабочих, чел.	Количество заводов	Число рабочих, чел.	Продукция, млн.руб.	Выработка на одного рабочего, тыс.руб.
1	700 - 1100	6	5230	3380	646,3
2	1100 - 1500	4	5390	6150	1141,0
3	1500 - 1900	4	8550	12550	1467,8
	Итого	15	19170	22080	1151,8

С увеличением числа рабочих на заводе увеличивается средняя выработка на одного рабочего.3адача 2. Выпуск продукции на заводе в 2020 г. составил 160 млн руб. По плану на 2021 г. предусматривалось выпустить продукции на 168 млн руб., фактически же выпуск составил 171,36 млн руб. Вычислите относительные величины планового задания и выполнения плана.Решение:Вычислим относительную величину планового задания по формуле:ОВПЗ= (Y_пл.з : Y_факт )* 100 = (168 : 160)* 100 = 105%.ОВВП₂₀₂₁ = Ф₂₀₂₁ / П₂₀₂₁ * 100 = 102%.В 2021 году план перевыполнен на 2%.Задача 3. На основании данных, представленных в таблице, определите установленную среднюю продолжительность трудового дня производственного рабочего по заводу в целом: 

Показатель	1 цех	2 цех	3 цех	4 цех
Количество смен	3	3	2	1
Число рабочих в смену	600	800	400	200
Продолжительность смены	8	8	8	6

---

Решение:Определим среднюю продолжительность трудового дня производственного рабочего по заводу по формуле средней гармонической взвешенной:X = M / ( M / X ) = (600 + 800 + 400 + 200) / (600 / 8 + 800 / 8 + 400 / 8 + 200 / 6) = 7, 74 (ч.)Ответ: Средняя продолжительность трудового дня рабочего 7, 74 ч.Задача 4. Имеются следующие данные о распределении рабочих цеха по размеру месячной заработной платы:

Размер зарплаты, тыс. руб.	до 5,0	5,0-7,5	7,5-10,0	10,0-12,5	свыше 12,5
Число рабочих, чел.	15	15	25	65	30

 Определите среднюю месячную зарплату рабочих цеха, моду и медиану, среднеквадратическое отклонение икоэффициент вариации.Решение:

1. 
   Средняя арифметическая:
   

X = X*f / fX= (5,0*15 + 6,25*15 + 8,75*25 + 11,25*65 + 12,5*30) / (15 + 15 + 25 + 65 + 30) = 9, 96Средняя месячная зарплата – 9, 96 тыс.руб.

2. 
   Мода – значение признака с наибольшей частотой.
   

М_о = 10,0 - 12,5 = 11, 25Мода = 11,25

3. 
   Медиана – середина ранжированного ряда.
   

Середина – 7,5-10 = 8,75Медиана = 8,75

4. 
   Среднеквадратичное отклонение можно определить, как квадратный корень из дисперсии:
   

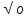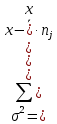
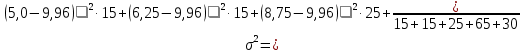
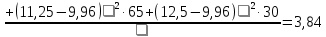
O = ²Найдем дисперсию: 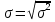= = 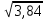1,96Среднеквадратичное отклонение= 1,96

5. 
   Коэффициент вариации найдем по формуле:
   

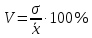
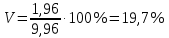
Коэффициент вариации=

---

19,7%

Задача 5. Объем продукции на промышленном предприятии повысился в 2016 году по сравнению с 2011 годом на 100 млн рублей в сопоставимых ценах, или на 25 %. В 2021 году объем продукции увеличился по сравнению с 2016 годом на 20 %.

Определите:

1) объем выпуска продукции предприятия в 2011, 2016, 2021 годах;

2) среднегодовые темпы прироста выпуска продукции за:  а) 2011-2021 гг.;     б) 2016-2021 гг.;     в) 2011-2016г. 

Решение:

Найдем объем выпуска продукции за:

2011год: 100:25(отношение 100млн.руб к 25%) = 400 млн.руб.

2016год: 400млн.руб + 100млн.руб = 500млн.руб.

2021 год: 500*1,2 = 600млн.руб.

Темп прироста высчитывается по формуле Т_{прироста} =Т_роста – 100

Чтобы найти темп прироста, надо найти темп роста. Он получается в результате деления уровня признака в определенный период или момент времени на уровень этого же показателя в предшествующий период или момент.
2011-2021:

i = 600:400 = 1,5*100 = 150% темп роста

Т_пр = Т_р – 100 = 150 – 100 = 50% темп прироста
2016-2021:

i = 600:500 = 1,2*100 = 120% темп роста

Т_пр = Т_р – 100 = 120 – 100 = 20% темп прироста
2011-2016:

i = 500:400 = 1,25*100 = 125% темп роста

Т_пр = Т_р – 100 = 125 – 100 = 25% темп прироста

Задача 6. По одному из предприятий промышленности стройматериалов имеются следующие данные:

 

Виды продукции	Снижение (–) или повышение (+) оптовых цен в отчетном периоде по сравнению с базисным (в %)	Реализовано продукции в отчетном периоде (тыс. руб.)
Строительные блоки	–2	1 960
Панели	+5	2 100
Строительные детали	без изменения	440

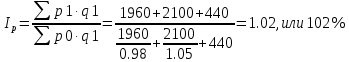
 Определите общий индекс цен и сумму роста или снижения объема реализации продукции за счет изменения цен.Решение:Общий индекс цен найдем по формуле:Цены выросли на 2%.

---

Смотрите также файлы

• Администрация городского округа Сухой лог Муниципальное бюджетное общеобразовательное учреждение.doc

• Гигиена в прямом смысле обозначает чистоту, является разделом медицины, который изучает влияние жизни и труда на здоровье человека и разрабатывающий меры (санитарные нормы и правила), направленные на предупреждение заболеваний, обеспечение оптимальных ус.docx

• Ознакомление с торговым предприятием и отделом (секцией).doc

• Приготовление воскресного обеда для всей семьи.docx

• 1. Адам мселесімен айналысатын гылым салалары.docx