Файл: Лабораторная работа 1 Персептроны. Аппроксимация функций Вариант 0 Фамилия Хамидов Имя Саид Отчество Хусейнович.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 39
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
Дисциплина: Нейросетевые технологии
Лабораторная работа №1
«Персептроны. Аппроксимация функций»
Вариант 0
Фамилия Хамидов
Имя Саид
Отчество Хусейнович
Группа УБ-01з
Санкт-Петербург
2023
Задание 1: смоделировать заданную функцию на отрезке [0, 8] с использованием библиотеки neuralnet. Отчет должен содержать подготовку данных для обучения сети. Обоснование выбранной архитектуры. Структурную схему обученной сети с указанием весов. Графики моделируемой и смоделированной функций.
Вариант 0: 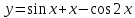
Ход работы
Нейросети подается на вход для обучения набор из 50 случайных чисел в диапазоне [0, 8], которые далее подставляются в выбранную нами функцию.

Листинг 1.
В результате перебора возможных архитектур сети выяснилось, что наиболее оптимальной и точной является архитектура с двумя скрытыми слоями, с количеством нейронов на первом слое равным 7, на втором равным 7. Эта архитектура выдает наименьший процент ошибки на заданном интервале, при этом быстро обучаясь.
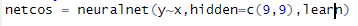
Листинг 2.
На рисунке 1 показана структурная схема обученной сети с указанием весов:
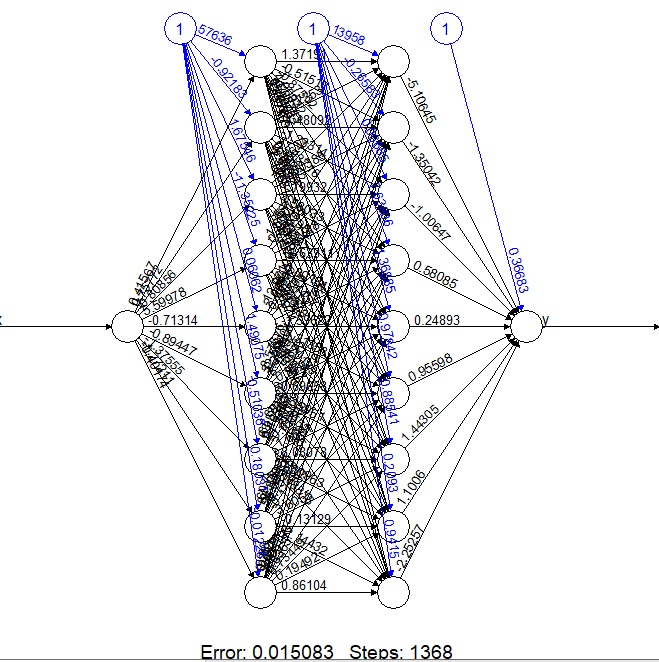
Рисунок 1 – Структурная схема обученной сети с указанием весов.
Рисунок 2 – График моделируемой функции.
На рисунке 3 представлен график моделируемой функции и смоделированной функции. Моделируемая функция – зеленые точки, смоделированная – черная линия
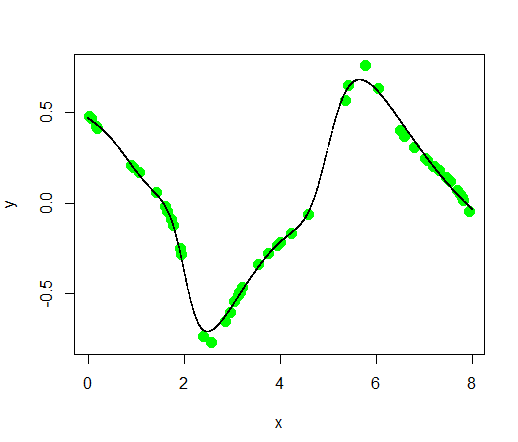
Рисунок 3 – График смоделированной функции – 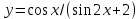
Код программы:
#Данные для обучения
set.seed(9)
x = runif(50,0,8)
y = cos(x)/(sin(2*x) + 2)
plot(x,y,pch=16,cex=1.5,col='green')
learn=data.frame(x,y)
#Библиотека + обучение netcos
library(neuralnet)
netcos = neuralnet(y
x,hidden=c(9,9),learn)
#Формирование тестовых данных и проверка сети netcos
set.seed(9)
x = runif(5000,0,8)
y = 0
test=data.frame(x,y)
yp = predict(netcos,test)
points(x,yp,col = 'black' ,pch='.', cex=1.5)
#выводим архитектуру сети
plot(netcos)
Задание 2: подобрать структуру hidden и порог функции ошибки threshold для точной аппроксимации заданных последовательностей импульсов. Отчет по работе должен содержать структурную схему обученной сети без указания весов. Графики аппроксимируемой и полученной последовательности для нескольких приближений параметров hidden и threshold.
Вариант0:
x = seq(from = -9.5, to = 10, by = 0.5)
y = rep(c(1,1,1,1,1,0,0,0,0,0), 4)
Ход работы
Создан набор данных для обучения нейронной сети, равный набору данных, по которым был построен график.

Листинг 3.
Была создана функция, которая по заданной архитектуре (количество скрытых слоев, количество нейронов на каждом слое, порог) обучает нейросеть и строит график.

Листинг 4.
Функция была вызвана 6 раз с различными аргументами. Получены 6 графиков:

Листинг 5.
На рисунке 4 представлены 6 графиков
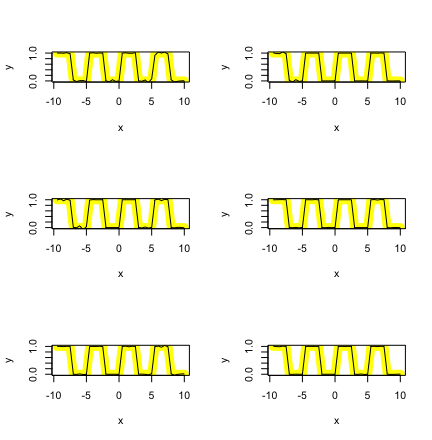
Рисунок 4 – графики с различными аргументами
Код программы:
install.packages('neuralnet')
library('neuralnet')
train = function(hid, thr) {
plot(x, y, type = "l", col = "yellow", lwd = 9)
net = neuralnet(y
x, hidden=hid, threshold=thr, learn)
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
Дисциплина: Нейросетевые технологии
Лабораторная работа №1
«Персептроны. Аппроксимация функций»
Вариант 0
Фамилия Хамидов
Имя Саид
Отчество Хусейнович
Группа УБ-01з
Санкт-Петербург
2023
Задание 1: смоделировать заданную функцию на отрезке [0, 8] с использованием библиотеки neuralnet. Отчет должен содержать подготовку данных для обучения сети. Обоснование выбранной архитектуры. Структурную схему обученной сети с указанием весов. Графики моделируемой и смоделированной функций.
Вариант 0:
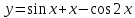
Ход работы
Нейросети подается на вход для обучения набор из 50 случайных чисел в диапазоне [0, 8], которые далее подставляются в выбранную нами функцию.

Листинг 1.
В результате перебора возможных архитектур сети выяснилось, что наиболее оптимальной и точной является архитектура с двумя скрытыми слоями, с количеством нейронов на первом слое равным 7, на втором равным 7. Эта архитектура выдает наименьший процент ошибки на заданном интервале, при этом быстро обучаясь.
Листинг 2.
На рисунке 1 показана структурная схема обученной сети с указанием весов:

Рисунок 1 – Структурная схема обученной сети с указанием весов.
Рисунок 2 – График моделируемой функции.
На рисунке 3 представлен график моделируемой функции и смоделированной функции. Моделируемая функция – зеленые точки, смоделированная – черная линия

Рисунок 3 – График смоделированной функции –
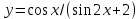
Код программы:
#Данные для обучения
set.seed(9)
x = runif(50,0,8)
y = cos(x)/(sin(2*x) + 2)
plot(x,y,pch=16,cex=1.5,col='green')
learn=data.frame(x,y)
#Библиотека + обучение netcos
library(neuralnet)
netcos = neuralnet(y
test = data.frame(x, 0)
y1 = predict(net, test)
lines(x, y1)
}
x = seq(from = -9.5, to = 10, by = 0.5)
y = rep(c(1,1,1,1,1,0,0,0,0,0), 4)
learn = data.frame(x, y)
par(mfrow = c(3, 2))
train(c(10, 10), 0.01)
train(c(15, 15), 0.01)
train(c(20, 20), 0.005)
train(c(25, 20, 25), 0.001)
train(c(25, 20, 10), 0.005)
train(c(20, 35, 20), 0.0005)
Вывод
В ходе выполнения лабораторной работы получены навыки построения заданной функции с использованием библиотеки neuralnet. Была представлена схема обученной модели с указанием весов, также предоставлен график моделируемой и смоделированной функций.
Также подобраны структура hidden и порог функции ошибки threshold для точной аппроксимации заданных последовательностей импульсов. Предоставлены графики аппроксимируемой и полученной последовательности для нескольких приближений параметров hidden и threshold.