ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 225
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1) протон 2) длина волны у всех перечисленных частиц одинакова
3) позитрон 4) нейтрон
5)
12.3.
Какая из перечисленных частиц: электрон, протон, нейтрон,
1) длина волны у всех перечисленных частиц одинакова
2) электрон 3) позитрон 4) нейтрон 5)
12.4.
Длина волны де Бройля
12.5.
Определите дебройлевскую длину волны электрона, ускоренного разностью потенциалов 100 В.( Масса электрона 10-30кг,
12.6.
Найти длину волны де Бройля для электрона
12.7.
Заряженная частица, ускоренная разностью потенциалов U = 200 B, имеет длину волны де Бройля 2,02 пм. Найти массу частицы, если ее заряд равен
1.668*10^-27 кг
12.8.
Какая единица длины волны де Бройля является основной в системе СИ?
1) 1 м 2) 1 Гц 3) 1 с 4) 1 рад/с
12.9.
Длина волны де Бройля может быть найдена по формуле:
1)
12.10.
Электрон и альфа-частица имеют одинаковые импульсы. Длина волны де Бройля какой частицы больше?
1) электрона, так как его электрический заряд меньше
2) альфа-частицы, так как ее масса больше
3) длины волн одинаковы
4) альфа-частица не обладает волновыми свойствами
13.Соотношение неопределенностей
13.1.
Какие из приведенных формул описывают соотношение неопределенностей?
А)
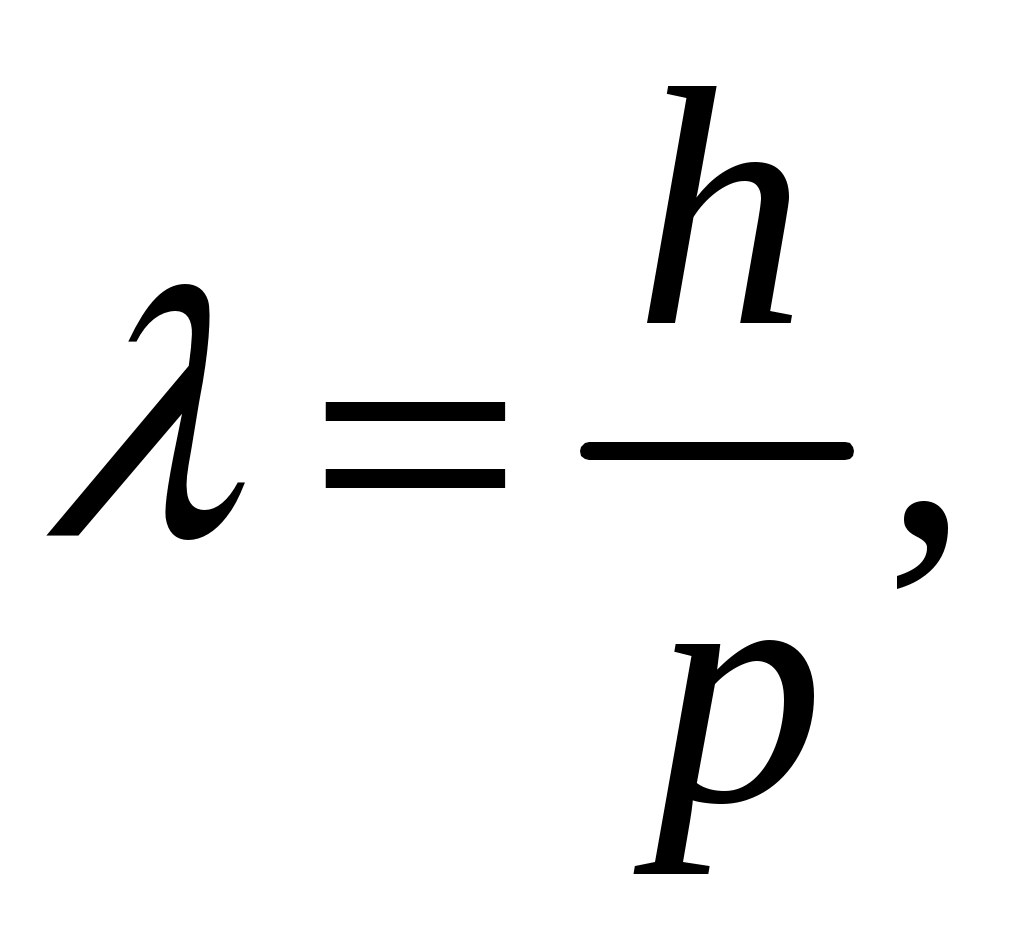 В)
В) D)
1) А 2) В, С, D, Е 3) А, В 4) А, В, С 5) Е
13.2.
Скорость протона (mp = 6,7∙10-27 кг), движущегося вдоль оси x, может быть измерена с погрешностью 10-6 м/с. Постоянная Планка
13.3.
Среднее время жизни атома в возбужденном состоянии
13.4.
Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, локализованного в области размером
13.5.
Оценить с помощью соотношения неопределенностей неопределенность скорости электрона в атоме водорода, полагая размер атома
13.6.
Электрон локализован в пространстве в пределах Δx = 1,0 мкм.
Постоянная Планка
Неопределенность в скорости составляет ΔVx (м/с) не менее…0,12*10^3
13.7.
Используя соотношение неопределенностей, оценить ширину одномерного потенциальной ямы, в которой минимальная энергия электрона равна 10 эВ. Постоянная Планка
13.8.
Время жизни атома в возбужденном состоянии t = 10 нс. Учитывая, что постоянная Планка
= 6,6×10-16 эВ·с, ширина энергетического уровня (в эВ) составляет не менее…6,6*10^-8
13.9.
Протон локализован в пространстве в пределах Δx = 1,0 мкм.
Постоянная Планка
Неопределенность в скорости составляет ΔVx (м/с) не менее…0,063 м /с
13.10.
Положение атома углерода в кристаллической решетке алмаза определено с неопределенностью Δx = 5 10-11 м. Учитывая, что постоянная Планка
14.Квантовые уравнения
14.1.
Для частицы, находящейся в потенциальном силовом поле с энергией
1)
3)
 4)
4) 
5)
14.2.
Уравнение Шредингера
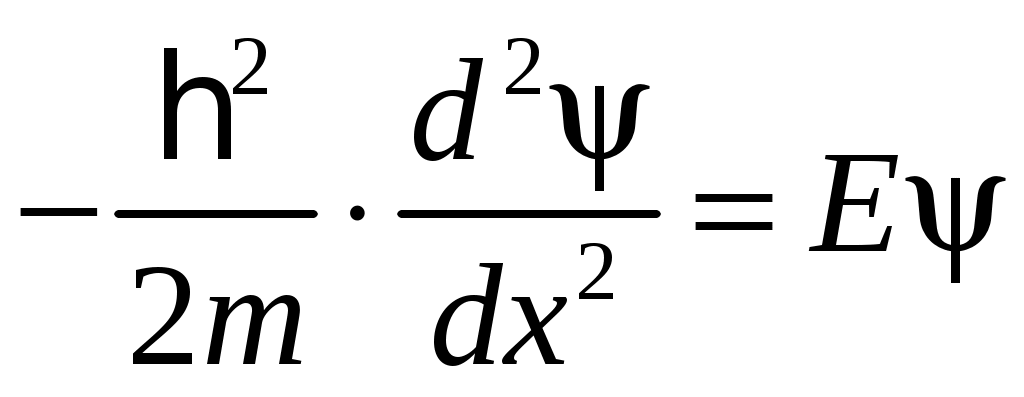 для свободно движущейся частицы имеет решение при значениях энергии Е, соответствующих выражению:
для свободно движущейся частицы имеет решение при значениях энергии Е, соответствующих выражению:1)
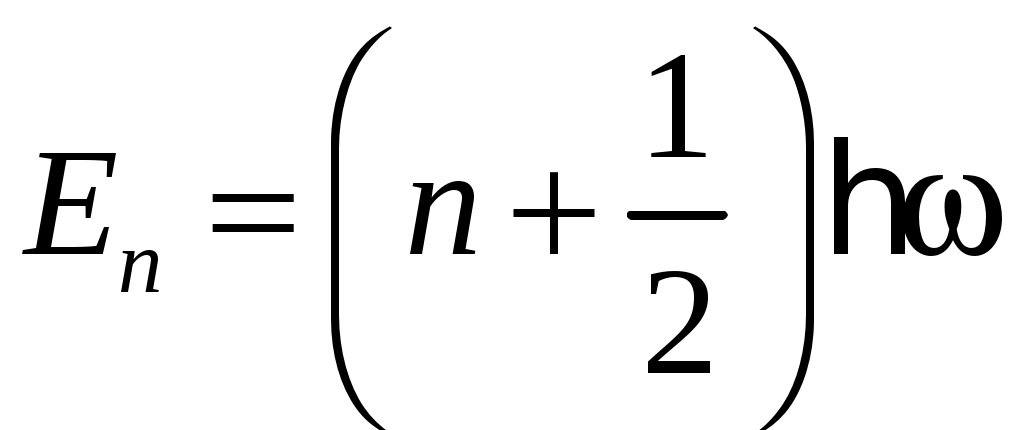 3)
3) 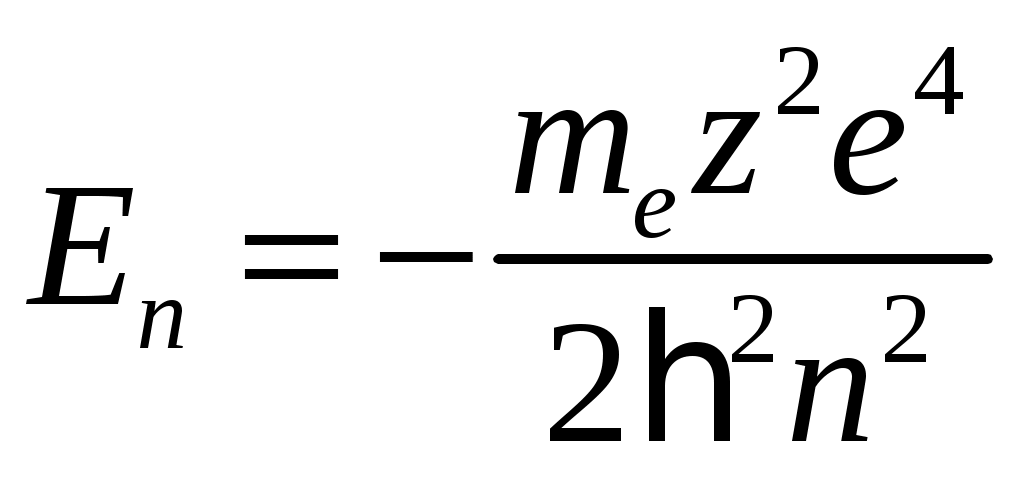
4)
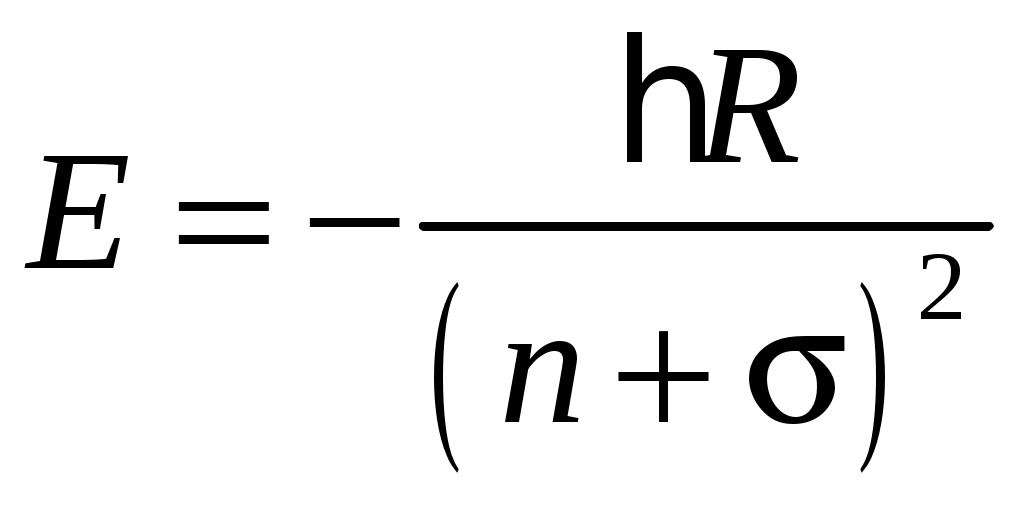 5)
5) 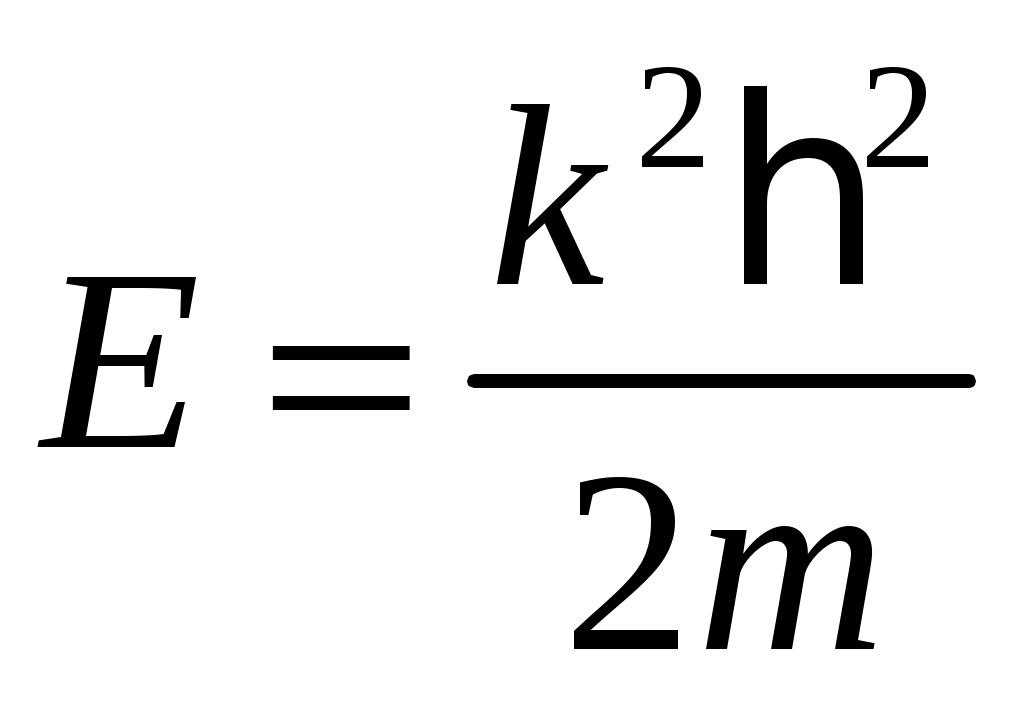
14.3.
Уравнение Шредингера
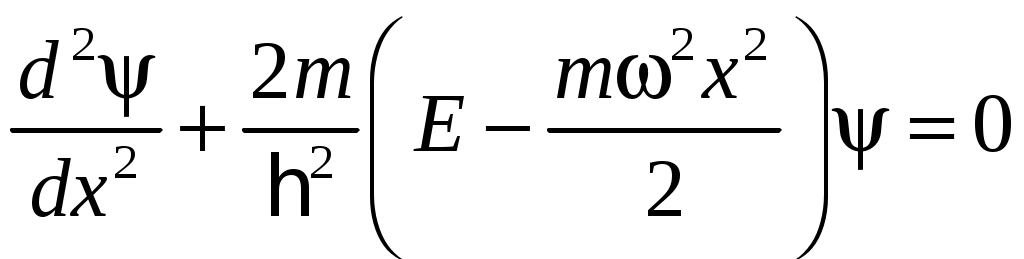 для квантового гармонического осциллятора имеет решение при значениях энергии
для квантового гармонического осциллятора имеет решение при значениях энергии
Е, соответствующих выражению:
1)
 3)
3) 
4)
 5)
5) 
14.4.
Уравнение Шредингера
1)
 3)
3) 
4)
 5)
5) 
14.5.
Уравнение Шредингера, имеющее вид
 , описывает:
, описывает:1) электрон, находящийся в одномерной бесконечно глубокой потенциальной яме
2) квантовый гармонический осциллятор
3) электрон в атоме водорода
4) прохождение электрона через потенциальный барьер (туннельный эффект)
5) электрон в двумерной потенциальной яме
14.6.
Нестационарным уравнением Шредингера является уравнение
А)
В)
1) A 2) Б 3) В 4) Г
14.7.
Оператор кинетической энергии в уравнении Шредингера имеет вид...
1)