Файл: Контрольная работа 2 Вариант Проверил доцент, к т. н. Новосибирск, 2023.doc

Федеральное государственное бюджетное образовательное учреждение высшего образования«Сибирский государственный университет телекоммуникаций и информатики»Кафедра высшей математикиКонтрольная работа № 2Вариант 7.Выполнил:Проверил:доцент, к.т.н.Новосибирск, 2023

Содержание

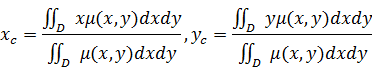
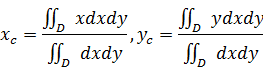
Задание 1. Кратные интегралыОднородная пластина имеет форму четырехугольника (см. рисунок). Указаны координаты вершин. С помощью двойного интеграла вычислить координаты центра масс пластины. Рисунок 1- ПластинаРешение. Координаты центра масс вычисляются по формулеТак как пластина однородная, то плотность ????=????????????????????, иСоставим уравнение прямой, ограничивающей область сверху. 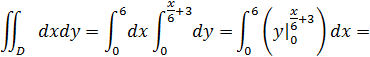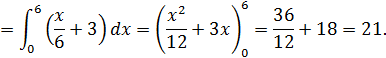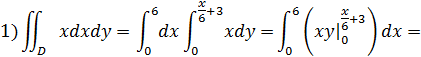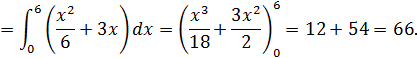Для этого достаточно знать две точки ) через которые она проходит:Координаты точек прямой, ограничивающей область сверху (0,3) и (6,4).Следовательно, уравнение прямой:Вычислим площадь пластины:Вычислим интегралы, которые фигурируют в числителях:Вычислим первую координату:

---

(Рисунок 2, слева)





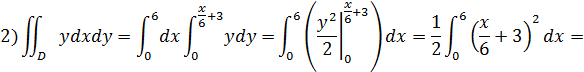
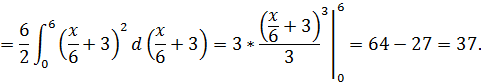
Вычислим вторую координату: (Рисунок 2, справа)



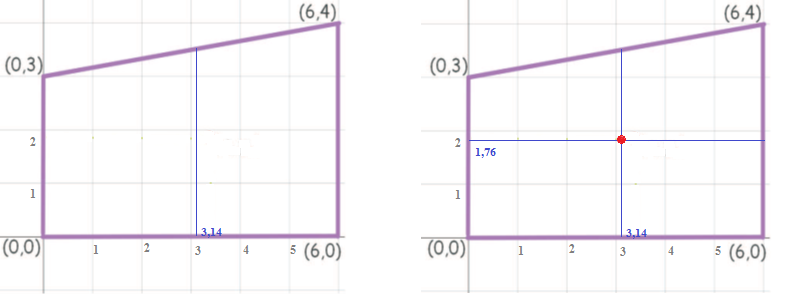
Рисунок 2 – Пластина с указанным центром масс

Ответ: координаты центра масс пластины (3,14;1,76)

Задание 2. Дифференциальные уравнения

Найти общее решение дифференциального уравнения . Решение. Определим тип уравнения. Раскроем скобки:делим обе части уравнения на :Данное уравнение является линейным, следовательно, для его решения можно воспользоваться заменой , (метод Бернулли): Найдём , приравнивая выражение в скобках к нулю: Найдем , при

---

Теперь, когда найдены оба сомножителя, можно записать общее решение уравнения : Ответ:

Задание 3. Степенные ряды

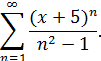
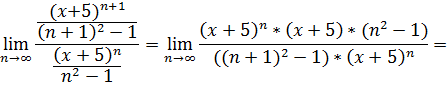
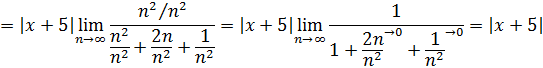
Найти область сходимости степенного ряда:Решение. Интервал сходимости ряда найдём с помощью признака Даламбера:Ряд сходится при , Следовательно, интервал является областью абсолютной сходимости ряда Исследуем сходимость ряда на концах найденного интервала:

1. 
   При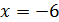 , степенной ряд преобразуется в числовой знакоположительный:
   

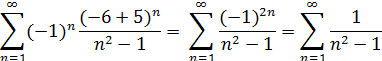
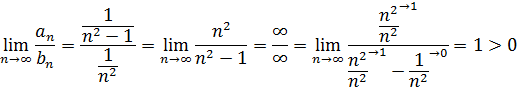
Сравним данный ряд со сходящимся рядом . Используем предельный признак сравнения.Получено конечное, отличное от нуля число, значит, при исследуемый ряд сходится.

2. 
   При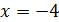 , степенной ряд преобразуется в числовой знакочередующийся:
   

---

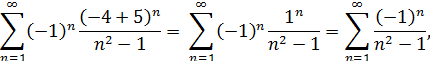
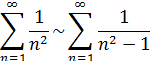
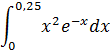
который сходится абсолютно по предельному признаку сравнения:Получено конечное, отличное от нуля число, значит, исследуемый ряд сходится при .Ответ: Ряд сходится при Задание 4. Приближенные вычисления с помощью разложения функции в рядВычислить с точностью до 0,001 значение определённого интеграла, разлагая подынтегральную функцию в степенной ряд:Решение. 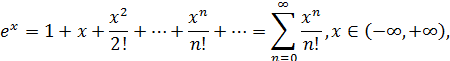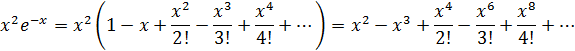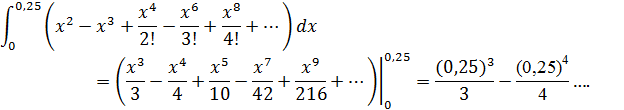Зная разложение в ряд Маклорена экспоненты запишем разложение :запишем разложение :Далее меняем подынтегральную функцию на полученный степенной ряд и вычисляем определенный интеграл:Второй член ряда меньше требуемой точности , поэтому мы отбрасываем его и все последующие. 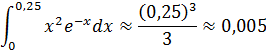Таким образом,Ответ: 0,005Задание 5. 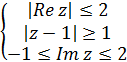Линии и области в комплексной плоскостиПо заданным условиям, построить область в комплексной плоскости.Решение.По определению,

---

Следовательно, условия принимают вид



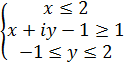
Рассмотрим каждое условие, поочерёдно добавляя к уже имеющимся:

вертикальная полоса (Рисунок 3, слева)

горизонтальная полоса (Рисунок 3, справа).

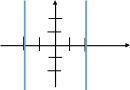-1 2 2 -1 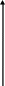2 -2 2

Рисунок 3- Точки, удовлетворяющие 1-му и 3-му условиямВычислим

---