Файл: Лабораторная работа 13 определение удельной теплоты кристаллизации и изменения энтропии при охлаждении сплава олова.doc

Лабораторная работа № 13

ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОТЫ КРИСТАЛЛИЗАЦИИ И ИЗМЕНЕНИЯ ЭНТРОПИИ ПРИ ОХЛАЖДЕНИИ СПЛАВА ОЛОВА

В настоящей работе экспериментально определяются изменение энтропии при фазовом переходе первого рода на примере кристаллизации олова (сплава олова со свинцом) из расплава при его охлаждении и удельная теплота кристаллизации из закона сохранения энергии.

1. Описание установки и метода измерений

Кристаллизация – процесс перехода вещества из жидкого состояния в твердое. Кристаллизация связана с выделением количества теплоты, равного теплоте плавления, и для химически чистых веществ протекает при постоянной температуре, равной температуре плавления.

В процессе кристаллизации упорядочивается движение частиц жидкости. Постепенно движение частиц превращается в связанные тепловые колебания около узлов кристаллической решетки.

Для начала кристаллизации необходимо, чтобы в жидкости имелись центры кристаллизации – неоднородности, вокруг которых начинается образование твердой фазы.

Если в жидкости отсутствуют центры кристаллизации, то она может быть охлаждена до температуры более низкой, чем температура плавления. Это состояние жидкости называется метастабильным.

Количество теплоты, которое необходимо отвести от единицы массы жидкости при температуре кристаллизации Т_к для перехода ее в твердое состояние, называется удельной теплотой кристаллизации _к. Согласно первому началу термодинамики,

_к = U_т – U_ж + p(V_т – V_ж), (1)

где U_т , U_ж – внутренняя энергия единицы массы в твердом и жидком состоянии; V_т, V_ж – удельный объем твердой и жидкой фаз; p– давление в процессе кристаллизации.

Поскольку p(V_т  V_ж) << U_т  U_ж,

_к  U_т – U_ж. (2)

Для характеристики состояния вещества используется понятие энтропии – функции состояния, определяемой с точностью до постоянной.

---

Разность энтропий в двух состояниях при обратимом процессе

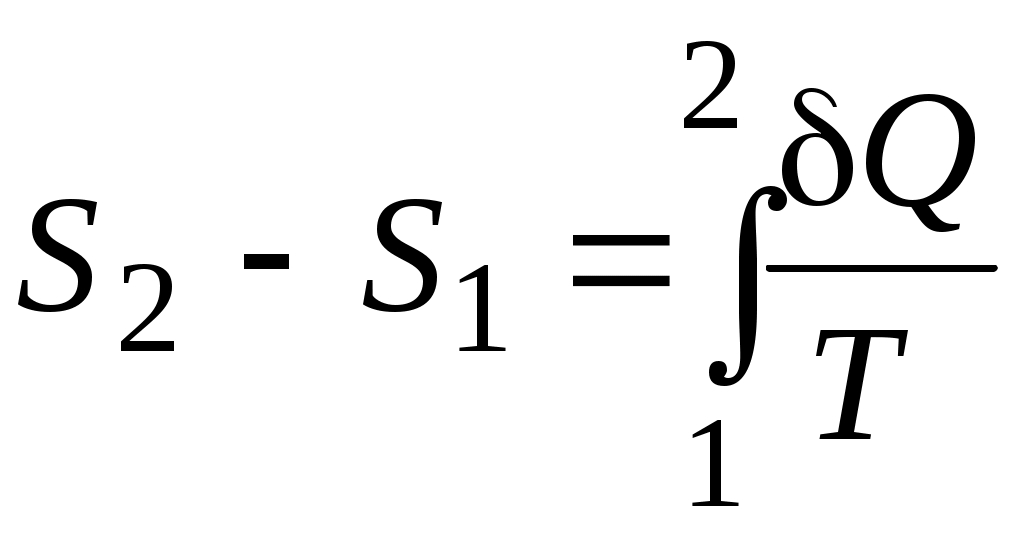, (3)

где – элементарное приведенное количество теплоты. В процессе кристаллизации вещество отдает количество теплоты Q окружающей среде при Т = const

(4)

где М_с – масса олова (или сплава).

Из (3) и (4) следует, что



или . (5)

В процессе кристаллизации происходит возрастание упорядоченности (создание структуры) молекул вещества, что приводит к убыванию энтропии системы.

Ампула со сплавом 2 (рис. 1) нагревается

в электрической печи 1, питающейся пере-

менным током. Внутри ампулы находит-

ся металлическая труба – чехол с диффе-

ренциальной хромель-копелевой термо-

парой, горячий спай 3 которой находится

в ампуле, а холодный 4 – на воздухе.

Концы термопары через гнезда и провода

соединены с милливольтметром 5, изме-

ряющем термоЭДС. Электрическая печь 1

находится в модуле экспериментального

стенда 6. Подключение электрической печи

к сети производится вилкой и тумблером 9

ВКЛ на стенде. Для подъема ампулы 2

необходимо отвинтить зажим 8 и пере-

местить ползунок 7 вверх.

Простейшей моделью охлаждения

тела является медленное охлаждение в

среде с постоянной температурой Т_с, когда

внутри тела в течение всего процесса

кристаллизации температура в любой

точке тела одинакова в любой момент

времени. Такой процесс состоит из

непрерывно следующих друг за другом

равновесных состояний и, следовательно,

является квазистационарным обратимым процессом.
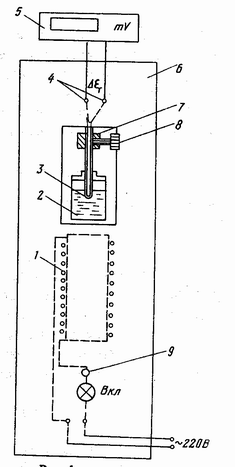Рис. 1

Применяя закон сохранения энергии к процессу охлаждения твердого сплава после кристаллизации, запишем

---

dT (C_с M_с + C_a M_a) +  F (T – T_c) d = 0, (6)

где dТ (С_с М_с + С_а М_а) < 0 – количество теплоты, отданное сплавом и ампулой среде при охлаждении за время d; F(T– T_c)d > 0 – количество теплоты, полученное окружающей средой через поверхность ампулы F за время d; C_с,C_a – удельные теплоемкости сплава и материала ампулы; M_с,M_a – массы сплава и ампулы; Т – температура твердого сплава; Т_c – температура окружающей среды;  – коэффициент теплоотдачи с поверхности ампулы в окружающую среду. Будем считать, что  – постоянная величина в течение всего опыта.

Применяя закон сохранения энергии к процессу кристаллизации сплава, можно получить уравнение

_к М_с +  F(Т_к – Т_с) = 0, (7)

где _кМ_с < 0 – количество теплоты, отданное сплавом при его кристаллизации окружающей среде за время  кристаллизации; F(Т_к–T_с) > 0 – количество теплоты, полученное окружающей средой через поверхность ампулы за время кристаллизации.

Из соотношений (6) и (7) получаем расчетную формулу для определения удельной теплоты кристаллизации

(8)

и изменения энтропии

. (9)

Следовательно, для определения S₂ – S₁ необходимо измерить температуру кристаллизации Т_к, время кристаллизации  и вычислить производную dT/d функции T = f() в точке, являющейся началом охлаждения твердого сплава после полной кристаллизации. Эти величины можно найти, измеряя температуру сплава в процессе охлаждения от полного расплава до температуры остывшего сплава Т_c в конце опыта.
2. Порядок выполнения работы

1. 
   Выписать данные установки.
   
2. 
   Включить стенд (рубильник на установке). При этом проверить, выключен ли тумблер электрической печи.
   
3. 
   Включить цифровой милливольтметр 5. Проверить его показания при выключенном нагревателе печи (на табло должны быть высвечены нули). Если его показания не равны нулю, подождать, пока сплав в ампуле охладится до комнатной температуры.
   
4. 
   Включить тумблер 9 электрической печи. Проследить в течение 10–15 мин. за тем, чтобы сплав, находящийся в ампуле, расплавился. Процесс плавления происходит при постоянной температуре Т_к, при этом показания милливольтметра не изменяются по величине. Конец плавления определяется после того, как показания милливольтметра начинают расти. Это значит, что температура расплавленного сплава начинает возрастать.
   
5. 
   Через 1 мин после конца плавления сплава отключить электрический нагреватель – тумблер 9 (показания милливольтметра не должны превышать 15 мВ, что соответствует температуре плавления термопары, нагрев выше указанной температуры недопустим!)
   
6. 
   Отвернуть винт 8 ползунка 7 и поднять ампулу со сплавом 2 из печи 1. Зафиксировать положение ампулы тем же винтом.
   
7. 
   Включить секундомер и через каждые 15 с снимать показания милливольтметра, фиксирующего разность температур сплава и окружающей среды. Измерения продолжить в течение 10 мин. Данные занести в табл. 1.
   

---

Зависимость  = f() изображена на рис. 2.

I - область полного расплава

II - область кристаллизации

III - область охлаждения твердого тела

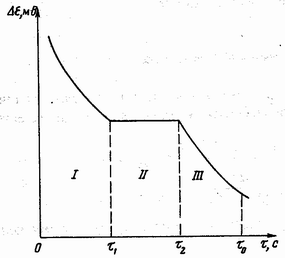
Рис. 2

 = ₂ – ₁ – время кристаллизации.

8. 
   Получив 40–50 экспериментальных точек, выключить вольтметр.
   

3. Обработка результатов измерений
Данные установки и таблицы результатов измерений:

Масса сплава М_с = ...

Масса ампулы М_а =...

Теплоемкость сплава С_с=...

Теплоемкость материала ампулы С_а=...

Температура окружающей среды t=..., °C.

ТермоЭДС _с, соответствующая температуре окружающей среды Т_с, берется из приложения 4.

Таблица 1

№ п/п	 ,с	, мВ	t, 0C	Т, К	(Т–Тс) = , К	ln 
1 2 3 . . .

1. Величину _к и S₂ – S₁ при кристаллизации сплава можно определить графической обработкой экспериментальных данных.

Математическая обработка данных

Согласно принятой модели, процесс охлаждения твердого сплава от точки полной кристаллизации описывается уравнением (6), решение которого есть

, (10)

где  = T– T_c;_к = T_к – T_c; .

Дифференцируя (10) по  и подставляя значение =₂ (₂ – время конца кристаллизации), получим

. (11)

Коэффициент m называется темпом охлаждения; характеризует относительную скорость изменения температуры в теле. Темп охлаждения можно определить из линейной зависимости, полученной логарифмированием функции (10):

---

ln  = ln _к – m(  ₂) . (12)

Для этого строится график зависимости ln  = f(₂) и по наклону графика определяется m (см. раздел «Графическая обработка результатов»).

Из (7), (10), (12) следует

, (13)

. (14)

Графическая обработка результатов
По полученным данным построить график зависимости  = f() и определить время кристаллизации сплава   ₂  ₁ (см.рис.2).

Определить по лабораторному термометру температуру окружающей среды–воздуха t_c и по приложению соответствующее ей значение термоЭДС _с хромель–копелевой термопары.

Прибавляя к каждому измеренному значению _i величину _с, определить по таблице температуру сплава t_i в процессе охлаждения в соответствующие моменты времени.

Определить _i = t_i– t_c и построить график зависимости ln = f( – ₂) для участка III (см. рис. 2), определить  .

Проведя «среднюю» прямую через экспериментальные точки, определить тангенс угла наклона

, (15)

где ₀ и ₀ – выбранные на графике значения разности температур и времени в конце опыта.

Рассчитать удельную теплоту кристаллизации по формуле

. (16)

Рассчитать изменение энтропии по формуле

. (17)

2. Рассчитать погрешность измерения _к из формулы

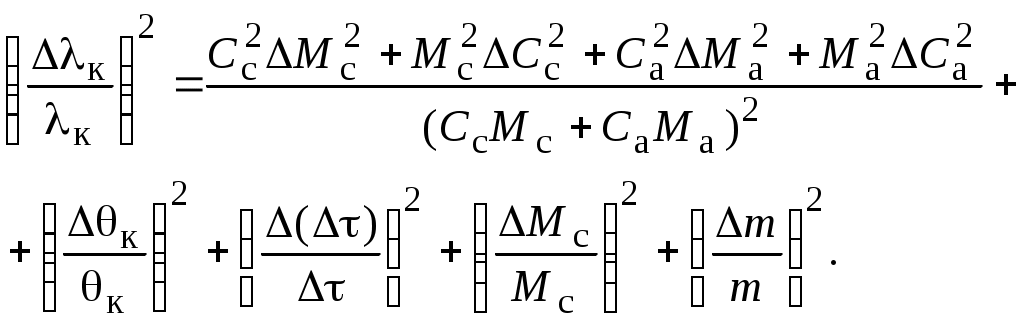(18)

При расчете погрешности можно пренебречь несущественными слагаемыми.

Считая, что относительные погрешности величин С_с, М_с, С_а, М_а, , _к

---