Файл: Отчет по Лабораторной работе 10 Определение модуля упругости (модуля Юнга) по деформации изгиба.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Отчет по практике

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 74

Скачиваний: 6

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ



МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ

Отчет по Лабораторной работе №10

«Определение модуля упругости (модуля Юнга) по деформации изгиба»


Выполнила: студент гр. ТХН-21-1 Теплов А.А

(шифр группы) (подпись) (Ф.И.О)

Проверил: _______________

(должность) (подпись) (Ф.И.О.) Оценка: ______________
Дата: ______________

Санкт Петербург

2022

Цель работы: Определить модуль Юнга материала путем измерения прогиба стержня при механической нагрузке.

Краткое теоретическое содержание Определения.

Деформация называется упругой, если она исчезает после прекращения действия силы. При упругой деформации, по закону, экспериментально установленному Гуком, величина абсолютной деформации Δl пропорциональна приложенной силе F:

???? = ????∆????

Где k – постоянная величина для данного образца.

Модуль Юнга – физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации.

Физический смыл модуля юнга – модуль Юнга численно равен нормальному напряжению, при котором длина деформируемого стержня изменилась бы в два раза.

Законы и соотношения, описывающие изучаемые процессы, на основании которых получены расчётные формулы.


Закон Гука при растяжении/сжатии стержня.

∆????/???? = 1/????*????/???? или ???? = ???? ????

где ???? = ∆????/???? – деформация или относительное изменение длины стержня;

???? = ???? ???? – нормальное механическое напряжение, [????] = Н/м2 ;

S – площадь поперечного сечения, [S] = м 2 ;

F – приложенная сила, [F] = Н;

l – первоначальная длина тела, [l] = м;

Δl – абсолютное удлинение стержня, [Δl] = м;

E – коэффициент пропорциональности (модуль Юнга), [E] = Н/м2 .

Схема установки.

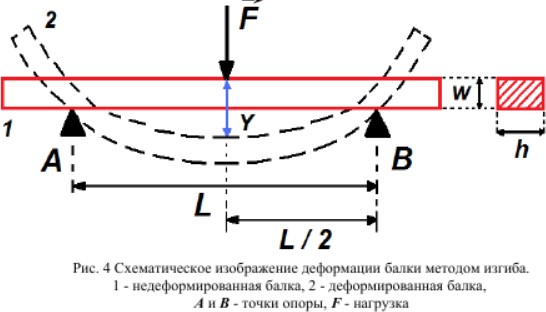
Расчетные формулы



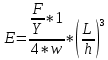
где F −приложенная в центре стержня сила, [F] = Н;

w, h – размеры поперечного сечения стержня, [w] = м, [h] = м;

Y – стрела прогиба стержня под нагрузкой, [Y] = м;

L – расстояние между опорами балки, [l] = м;

E – модуль Юнга, [E] = Н/м2.

Формула для расчета погрешностей косвенных измерений

Абсолютная погрешность измерений модуля Юнга.



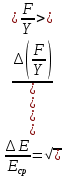
w, h – размеры поперечного сечения стержня, [w] = м, [h] = м;

L – расстояние между опорами балки, [L] = м;

E – модуль Юнга, [E] = Н/м2;

Δw, Δh – погрешность прямых измерений размеров поперечного сечения стержня, [Δw] = м, [Δh] = м;

ΔL – погрешность прямых измерений расстояния между опорами балки, [ΔL] = м;

- среднее значение F/Y; [F/Y] = Н/м

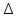F/Y - погрешность измерения величины F/Y; [ 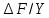] = Н/м

Погрешность прямых измерений:

Погрешность измерения массы грузов, Δm = 0,1 г;

Погрешность измерения стрелы прогиба, ΔY = 0,01 мм;

Погрешность измерения размеров поперечного сечения стержня, Δw = Δh = 0,05мм

Погрешность измерения расстояния между опорами балки, ΔL = 1 мм.

Таблица №1: Измерение размеров поперечного сечения бруска

№
h
hср
Δh
w
wср
Δw

№оп ед
мм
мм
мм
мм
мм
мм

1
3,8
3,88
0,05
12,1
12,11
0,05

2
3,9
12,0

3
4,0
12,2

4
3,6
12,1

5
4,0
12,0

6
3,9
12,1

7
3,8
12,3

8
4,0
12,2

9
3,8
12,0

10
4,0
12,1

Таблица 2: Результаты измерений и вычислений

№
Масса
F
n
Y
F/Y


E

№оп ед
кг
Н
делений
м
Н/м
Н/м
Н/м^2

1
0,1
0,98
19
0,19*10^-3
5157,9
4922,92
10*10^10

2
0,2
1,96
39
0,39*10^-3
5025,64
97,5*10^9

3
0,4
3,92
79
0,79*10^-3
4962,02
96,26*10^9

4
0,65
6,37
129
1,29*10^-3
4937,98
95,79*10^9

5
1,169
11,4562
229
2,29*10^-3
5002,7
97,05*10^9

6
1,474
14,4452
287
2,87*10^-3
5033,17
97,64*10^9

7
1,169
11,4562
230
2,3*10^-3
4980,95
96,63*10^9

8
0,65
6,37
129
1,29*10^-3
4937,98
95,79*10^9

9
0,4
3,92
82
0,82*10^-3
4780,49
92,74*10^9

10
0,2
1,96
42
0,42*10^-3
4666,67
90,53*10^9

11
0,1
0,98
21
0,21*10-3
4666,67
90,53*10^9

Расчеты

1. Исходные данные: дан металлический стержень( балка);

Расстояние между опорами балки l = 380 мм;

Погрешность прямых измерений Δm = 0,5 г;

ΔY = 0,01 мм;

Δw = Δh = 0,05 мм;

ΔL = 1 мм.

2. Вычисления:

К таблице 1.

Расчет средних значений поперечного сечения стержня.

hср = =

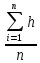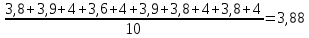
wср =

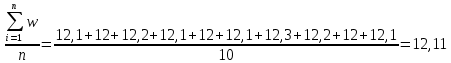
К таблице 2.

Пример вычисления для опыта №1.

Расчет силы, действующей на балку.

???? = ???????? = 9,8 ∙ 0,1= 0,98 Н

Стрела прогиба балки.

???? = 0,01 ∙ ???? = 0,01 ∙ 19 = 0,19 мм = 0,19 ∙ 10−3 м

Значение F/Y

F/Y=0,98/0,19 ∙ 10−3 = 5157,9 Н/м

Модуль Юнга для стержня.

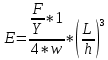= 5157,9* 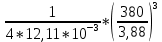= 10*10^10 Н/м^2

Среднее значение F/Y

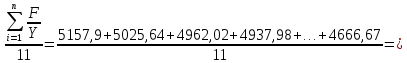= 4922,92 Н/м

Среднее значение модуля Юнга для стержня.

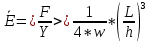= 4922,92*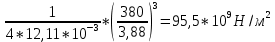

Относительная погрешность измерений модуля Юнга.

=

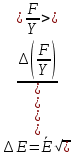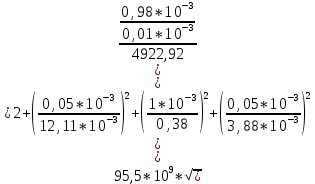
Результат: Модуль Юнга с учетом абсолютной погрешности косвенных измерений

E =

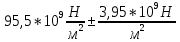
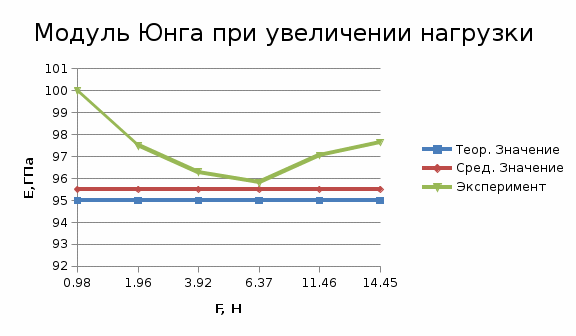
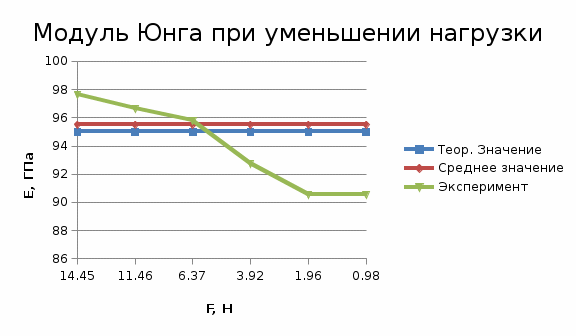
Сравнительная оценка результата


Полученное значение модуля Юнга наиболее приближено к модулю Юнга латуни (Ел = 95∙109 Н/м2).



Сравнительная оценка результата

Полученное значение модуля Юнга наиболее приближено к модулю Юнга латуни (Ел = 95∙10^9 Н/м2).

%=
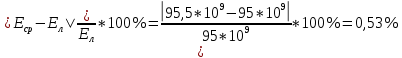
Вывод

В ходе лабораторной работы удалось установить модуль Юнга для металлического стержня методом прогиба балки под нагрузкой. Наиболее приближенным теоретическим значением к экспериментальному значению оказался модуль Юнга латуни. Расхождение экспериментального результата с теоретическим составило 0,53%.

Данная погрешность косвенных измерений объясняется тем, что мы пользовались механическим стрелочным манометром. В данном приборе присутствует трение механизмов, которое иногда не позволяет точно определить стрелу прогиба. Также мы не можем утверждать, что работали со стержнем, у которого нет внутренних дефектов, которые могут влиять на значение ходуля Юнга материала.

Несмотря на эти причины погрешности методика измерения модуля Юнга достаточно точная.

Смотрите также файлы